
13.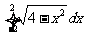 =________.
=________.
12.定义:若数列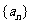 对任意的正整数n,都有
对任意的正整数n,都有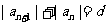 (d为常数),则称
(d为常数),则称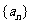 为“绝对和数列”,d叫做“绝对公和”,已知“绝对和数列”
为“绝对和数列”,d叫做“绝对公和”,已知“绝对和数列”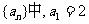 ,“绝对公和”
,“绝对公和”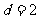 ,则其前2010项和
,则其前2010项和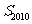 的最小值为( )
的最小值为( )
A.-2010 B.-2009 C.-2006 D.-2011
第Ⅱ卷(非选择题 共90分)
11. 的值为( )
的值为( )
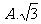
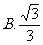
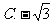

10.定义在R上的函数f(x)满足f(x)= 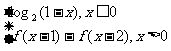 ,则f(2011)的值为( )
,则f(2011)的值为( )
A.0 B.1 C.-1 D.2
9.使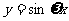 (ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )
(ω>0)在区间[0,1]至少出现2次最大值,则ω的最小值为( )
A. B.
B.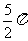 C.π D.
C.π D.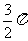
8.已知点O是△ABC所在平面内的一定点,P是平面ABC内一动点,若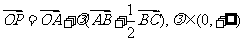 ,则点P的轨迹一定经过△ABC的( )
,则点P的轨迹一定经过△ABC的( )
A. 垂心 B. 重心 C. 内心 D. 外心
7.在△ABC中,若cosA·cosB>sinA·sinB,则△ABC为( )
A. 锐角三角形 B. 钝角三角形C. 直角三角形 D. 不能确定
6.等比数列{an},已知对于任意的自然数n,
a1+a2+a3+…+an=2n-1,则a12+a22+a32+…+an2等于( )
A.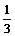 (4n-1) B.
(4n-1) B.
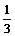 (2n-1) C. 4n-1 D. (2n-1)2
(2n-1) C. 4n-1 D. (2n-1)2
5.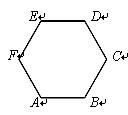 如图,已知正六边形ABCDEF,下列向量的数量积中最大的是( )
如图,已知正六边形ABCDEF,下列向量的数量积中最大的是( )
A. 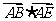 B.
B. 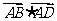
C.
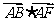 D.
D. 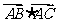 .
.
4.已知向量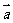 =(-2,1),
=(-2,1),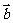 =(-3,0),则
=(-3,0),则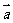 在
在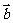 方向上的投影为( )
方向上的投影为( )
A.-2
B.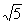 C.2
D.-
C.2
D.-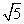
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com