
(二)空间两条直线
1.空间两直线的位置关系有:
(1)相交; (2)平行;
(3)异面.定义--
2 公理4 :平行于同一条直线的两条直线互相平行.
3 等角定理:一个角的两边和另一个角的两边分别平行且方向相同,则这两个角相等.
推论:两条相交直线和另两条相交直线分别平行,则这两条直线所成的角相等.
4 空间两条异面直线:不同在任何全个平面内.
空间两条异面直线:不同在任何全个平面内.
判定定理:过平面内一点与平面外一点的直线,和这个平面内不经过此点的直线是异面直线.
5.异面直线所成的角的求法:
找(或)作出过一条直线上一点,于另一直线平直线;或过空间一点与两条直线平行的直线,转化为平面内的角,再用平面几何的方法去求;也可用向量法.
注意:两条直线所成的角的范围: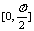 . 两条异面直线所成的角的范围:
. 两条异面直线所成的角的范围: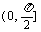 .
.
6 两条异面直线的公垂线、距离
和两条异面直线都垂直且相交的直线,我们称之为异面直线的公垂线.
理解:和异面直线都垂直的直线有无数条,公垂线只有一条.
两条异面直线的公垂线在这两条异面直线间的线段(公垂线段)的长度,叫做两条异面直线间的距离.
计算方法:①几何法;②向量法
(一)平面的概念和性质
1.平面的概念:平面是没有厚薄的,可以无限延伸.
2.空间点、线、面的位置关系及表示:要正确运用下列符号:
点A,B,C,…;直线 a,b,c,…;平面α,β,γ…
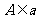 ,
,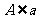 ,
,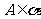 ,
, ,
,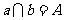 ,
,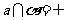 ,a∥b,a⊥b,a∥α,a⊥β, α⊥β, α//β, α⊥β, α∩β=a
,a∥b,a⊥b,a∥α,a⊥β, α⊥β, α//β, α⊥β, α∩β=a
3.平面的基本性质
公理1.线的在平面内.
用途:判定直线在平面内,验证是否平面.
公理2两个平面的交线.
用途:①确定两相交平面的交线;②判定点在直线上.
公理3及其三个推论: 确定平面的条件.
注意“确定”即“有且只有一个”的含义.
4.所有点都在一个平面内的图形称为平面图形,否则称为空间图形.
3.能进行简单的文字、符号、图形三者之间的转化.
2.掌握空间两直线的位置关系,理解异面直线的定义,能证明和判断两条直线是异面直线.能用图形表示两条直线的位置关系,会解决与位置关系有关的问题.
1.掌握平面的基本性质,会运用这些性质解决有关共面、共线、共点、交线等问题.
7.已知函数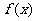 满足
满足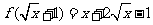 ,求函数
,求函数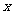 的解析式.
的解析式.
错解:由已知得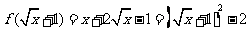 ,所以
,所以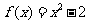 ;
;
正解:由已知得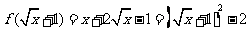 ,因为
,因为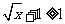 ,所以函数的解析式为
,所以函数的解析式为 .
.
错误原因:在换元法求解析式时,要注意新元的取值范围,即函数的定义域问题.
6.已知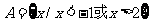 ,
,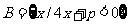 ,且B为A的真子集,则实数p的取值范围是_____________.
,且B为A的真子集,则实数p的取值范围是_____________.
错解: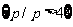 ,
,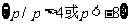 等
等
正解: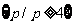
错误原因:(1)忽视数形结合思想方法的体现,画出数轴,结合真子集的定义,只需比较-1与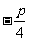 的大小,有些同学误认为
的大小,有些同学误认为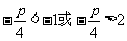 ;
;
(2)对端点处的取值能否相等考虑不仔细,实际上本题中-1与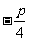 可以取到相等,即
可以取到相等,即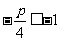 .
.
5.对于从A到B的函数f(x)下列四种说法中,正确的是_________.
(1)在B中的每一个数,在定义域A中都有至少一个数与之对应;
(2)集合A、B一定是无限集合;
(3)定义域和对应关系确定后,函数的值域也就确定了;
(4)若函数的定义域中只含有一个元素,则值域也只含有一个元素.
错解:(1)(3)(4)
正解:(3)(4)
错误原因:函数的对应法则的要求是:A中的任意一个元素在B中都有唯一确定的元素与之对应,但B中可以有剩余元素不参与与A中的元素对应,即B不是函数的值域,所以(1)不正确。
4.下列各组函数表示相同函数的是__________.
(1)
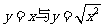 (2)
(2)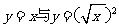 (3)
(3)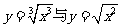
(4)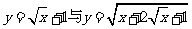 (5)
(5)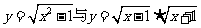
错解:(1)(2)(4)(5)
正解:(4)
错误原因:
(1)中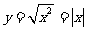 ,二者的对应法则不同,所以不是相同函数;
,二者的对应法则不同,所以不是相同函数;
(2)中第一个函数的定义域为R,第二个函数的定义域为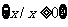 ,定义域不同,所以不是相同函数;
,定义域不同,所以不是相同函数;
(5)中第一个函数的定义域为 ,第二个函数的定义域为
,第二个函数的定义域为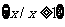 ,定义域不同,所以不是相同函数.
,定义域不同,所以不是相同函数.
3.已知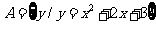 ,
,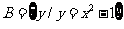 ,则
,则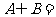 ___________.
___________.
错解: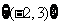 ,
,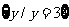 等等
等等
正解: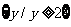
错误原因:没有理解题目中的两个集合的含义,描述法的实质在于认清代表元素所具备的性质,上述两个集合中的y为函数值,集合是函数值的集合即函数的值域,所以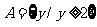
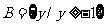 ,故
,故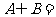
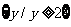 .
.
类似问题:
已知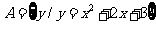 ,
,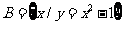 ,则
,则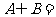 ___________.
___________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com