
24.选修4-5:不等式选讲
设函数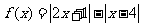 .
.
(1)解不等式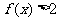 ;
;
(2)求函数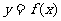 的最小值.
的最小值.
23.选修4-4:坐标系与参数方程
已知曲线C1的极坐标方程为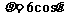 ,曲线C2的极坐标方程为
,曲线C2的极坐标方程为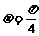 (
(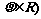 ,曲线C1,C2相交于点A,B。
,曲线C1,C2相交于点A,B。
(1)将曲线C1,C2的极坐标方程化为直角坐标方程;
(2)求弦AB的长。
22.选修4-1:几何证明选讲
如图,圆O的直径AB=10,弦DE⊥AB于点H,AH=2。
(1)求DE的长;
(2)延长ED到P,过P作圆O的切线,
切点为C,若PC=2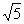 ,求PD的长。
,求PD的长。
21.(本小题满分14分)
等差数列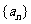 的各项均为正数,
的各项均为正数,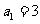 ,前
,前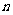 项和为
项和为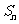 ,
,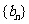 为等比数列,
为等比数列, 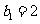 ,且
,且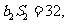
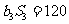 .
.
(1)求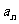 与
与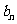 ;
;
(2)求数列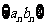 的前
的前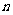 项和
项和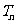 。
。
(3)若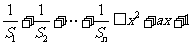 对任意正整数
对任意正整数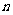 和任意
和任意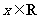 恒成立,求实数
恒成立,求实数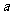 的取值范围.
的取值范围.
20.(本小题满分14分)
已知函数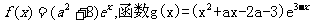
(1)若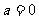 ,求
,求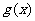 的单调递减区间;
的单调递减区间;
(2)若 ,且存在
,且存在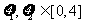 使得
使得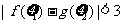 ,求实数
,求实数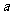 的取值范围。
的取值范围。
19.(本题满分12分)
已知角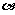 的顶点在原点,始边与
的顶点在原点,始边与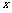 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点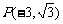 .
.
(1)求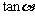 的值;
的值;
(2)定义行列式运算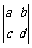
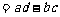 ,求行列式
,求行列式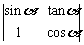 的值;
的值;
(3)若函数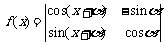 (
(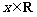 ),求函数
),求函数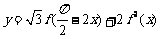 的最大值,并指出取到最大值时
的最大值,并指出取到最大值时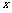 的值.
的值.
18.(本题满分10分)
设向量 =
=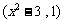 ,
,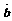 =
=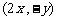 (其中实数
(其中实数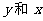 不同时为零),当
不同时为零),当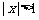 时,有
时,有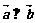 ;当
;当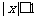 时,有
时,有 ∥
∥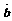 .
.
(1)求函数解析式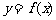 ;
;
(2)设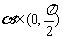 ,且
,且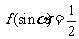 ,求sin
,求sin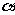 .
.
证明过程或演算步骤.
17.(本小题满分10分)
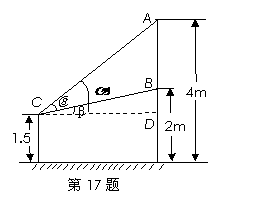
如图,有一壁画,最高点A处离地面4m,最低点
B处离地面2m,若从离地高1.5m的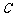 处观赏它,则
处观赏它,则
离墙多远时,视角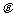 最大?
最大?
16.给出下列命题:
①常数列既是等差数列,又是等比数列;
②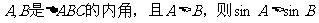 ;
;
③在数列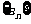 中,如果
中,如果 前项和
前项和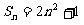 ,则此数列是一个公差为4的等差数列;
,则此数列是一个公差为4的等差数列;
④若向量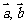 方向相同,且
方向相同,且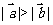 ,则
,则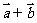 与
与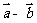 方向相同;
方向相同;
⑤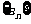 是等比数列,
是等比数列,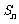 为其前
为其前 项和,则
项和,则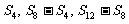 成等比数列。
成等比数列。
 则上述命题中正确的有
. (填上所有正确命题的序号)。
则上述命题中正确的有
. (填上所有正确命题的序号)。
15.2002年在北京召开的国际数学家大会,会标是以我国古代数学家赵爽
的弦图为基础设计的.弦图是由四个全等直角三角形与一个小正方形
拼成的一个大正方形(如图).如果小正方形的面积为1,大正方形的
面积为25,直角三角形中较小的锐角为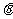 ,那么
,那么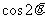 的值等于 .
的值等于 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com