
2.若关于 的方程
的方程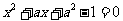 有一正根和一负根,则
有一正根和一负根,则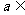 .
.
1.若不等式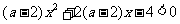 对一切
对一切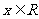 成立,则
成立,则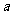 的取值范围是
.
的取值范围是
.
例1.解下列不等式:
(1)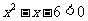 ;(2)
;(2)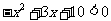 ;(3)
;(3)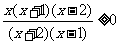 .
.
例2.已知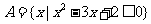 ,
,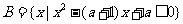 ,
,
(1)若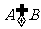 ,求
,求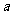 的取值范围;
的取值范围;
(2)若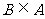 ,求
,求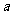 的取值范围.
的取值范围.
例3.已知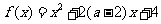 ,
,
(1)如果对一切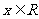 ,
,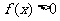 恒成立,求实数
恒成立,求实数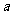 的取值范围;
的取值范围;
(2)如果对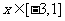 ,
,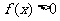 恒成立,求实数
恒成立,求实数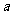 的取值范围.
的取值范围.
例4.已知不等式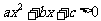 的解集为
的解集为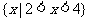 ,则不等式
,则不等式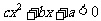 的解集为
.
的解集为
.
例5.已知二次函数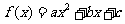 的图象过点
的图象过点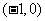 ,问是否存在常数
,问是否存在常数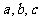 ,使不等式
,使不等式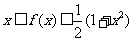 对一切
对一切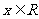 都成立?
都成立?
考题1(2005福建)不等式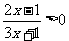 的解集是 (
)
的解集是 (
)
A.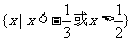 B.
B.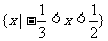
C.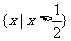 D.
D.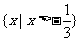
考题2
(2004天津)不等式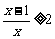 的解集为(
).
的解集为(
).
A. 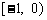 B.
B.
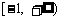 C.
C.
 D.
D.
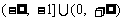
考题3(2005浙江理)已知函数f(x)和g(x)的图象关于原点对称,且f(x)=x2=2x.
(Ⅰ)求函数g(x)的解析式;
(Ⅱ)解不等式g(x)≥f(x)-|x-1|.
考题4(2006全国II文)设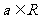 ,函数
,函数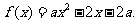 若
若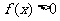 的解集为A,
的解集为A,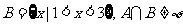 ,求实数
,求实数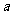 的取值范围。
的取值范围。
考题5(2001江西、山西、天津理)解关于x的不等式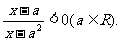
4. 几点注意:①含参数的不等式要善于针对参数的取值进行讨论;
②要善于运用“数形结合”法解决有关不等式问题;
③要深刻理解不等式的解集与对应方程的解之间的关系,会由解集确定参数的值。
3.高次不等式主要是利用“数轴轴标根法”解.
2.分式不等式主要是转化为 ,再用数轴标根法求解。
,再用数轴标根法求解。
1.解一元二次不等式通常先将不等式化为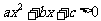 或
或 的形式,然后求出对应方程的根(若有根的话),再写出不等式的解:大于
的形式,然后求出对应方程的根(若有根的话),再写出不等式的解:大于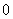 时两根之外,小于
时两根之外,小于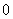 时两根之间;或者利用二次函数的图象来写出一元二次不等式的解集。
时两根之间;或者利用二次函数的图象来写出一元二次不等式的解集。
3.高次不等式的基本解法、要注重对重因式的处理.
2.分式不等式的基本解法、要注意大于等于或小于等于的情况中,分母要不为零;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com