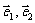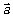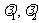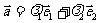6.平面向量的基本定理：如果是一个平面内的两个不共线向量，那么对这一平面内的任一向量，有且只有一对实数使：其中不共线的向量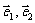叫做表示这一平面内所有向量的一组基底.

5.向量共线定理：

向量与非零向量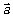共线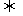

怎样判定向量共线--(1)共线向量定理；(2)依定义; (3)用几何方法.

4.实数与向量的积

(1)实数λ与向量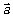的积：①是个向量;②模等于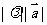③方向λ>0时与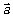同向,λ<0时与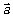反向.

(2)数乘向量满足交换律、结合律与分配律。

3.向量的减法

(1)相反向量：

关于相反向量有：　 ①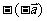=；　 ②+()=()+=；

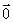③若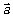、是互为相反向量，则=,=,+=。

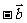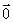(2)向量减法：向量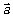加上的相反向量叫做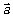与的差，记作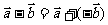：。求两个向量差的运算，叫做向量的减法。

如上图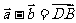表示为从的终点指向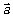的终点的向量(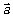、有共同起点)。

(3)温馨提示：①用平行四边形法则时，两个已知向量是要共始点的，和向量与差向量分别是两条对角线,注意方向。

②三角形法则的特点是“顺次首尾相接”由此可知,封闭折线的向量和为零.

差向量是从减向量的终点指向被减向量的终点。

2.向量加法:　 设，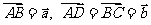

(1)求两个向量和的运算叫做向量的加法，向量加法按“平行四边形法则”或“三角形法则”进行。

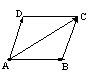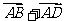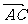　如图 +==。 或 　+=

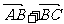
　规定：；　

(2) 向量加法满足交换律与结合律；　　　　　　　　　　　　　　　　　　　　　

1.向量的有关概念

(1)向量：既有大小又有方向的量.

可用有向线段表示.记作: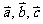…或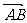…等；向量的长度即向量的模记作||。

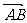(2)零向量：　　　　　　　　　　　　　 其方向：

(3)单位向量：　　　　　　　　　　　　 单位向量不唯一.

(4)平行向量(共线向量)：方向相同或相反方向相同或相反.

规定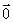：与任意向量平行。

(5)相等向量：长度相等且方向相同.

1理解向量的概念，掌握向量的几何表示，了解共线向量的概念　　

2掌握向量的加法和减法

3掌握实数与向量的积;理解两个向量共线的充要条件 　　　

12、若不等式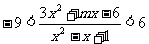对一切x恒成立,求实数m的范围

11、已知关于x的不等式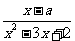≥0的解集为{x| 1<x≤a或x>2}，则a的取值范围是　　 .

10、已知(a+b)x+(2a－3b)<0的解为{x| x<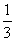－}，则不等式(a－3b)x+b－2a>0的解集为　　　 .