
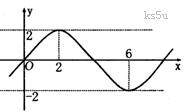
3、(四川省成都市新都一中高2008级一诊适应性测试)函数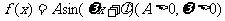 的图象如图所示,则
的图象如图所示,则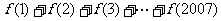 的值等于
.
答案:0
的值等于
.
答案:0
2、(四川省巴蜀联盟2008届高三年级第二次联考)关于函数f (x) =sin(2x-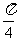 )(x∈R) 有下列命题:
)(x∈R) 有下列命题:
① y=f(x)的周期为π;
② x =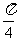 是y = f (x)的一条对称轴;
是y = f (x)的一条对称轴;
③(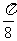 ,0)是y=f(x)的一个对称中心;
,0)是y=f(x)的一个对称中心;
④ 将y = f(x)的图象向右平移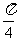 个单位,可得到y=2sinxcosx的图象
个单位,可得到y=2sinxcosx的图象
其中正确的命题序号是 (把你认为正确命题的序号都写上).
 答案:①③
答案:①③
1、(广东省广州执信中学、中山纪念中学、深圳外国语学校三校期末联考)在平面直角坐标系xoy中已知△ABC的顶点A(-6,0) 和C(6,0),顶点B在双曲线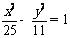 的左支上,
的左支上,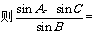
答案: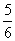
10. 求证ΔABC的三条中线AD、BE、CF交于一点,并确定交点在中线上的位置。
 证明:设
证明:设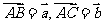 ,AD,BE交于点G,
,AD,BE交于点G,
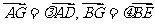 ,在ΔACG中,由
,在ΔACG中,由
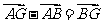 ,可得
,可得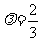 .
.
同理可证,AD,CF也交于G点,G在AD的三分点处.
[探索题]在△ABC中,AM∶AB=1∶3,AN∶AC=1∶4,BN与CM交于点E,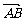 =a,
=a,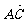 =b,用a、b表示
=b,用a、b表示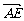 .
.
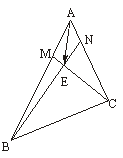 解:由已知得
解:由已知得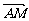 =
=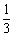
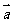 ,
,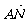 =
=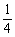
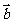 .
.
设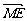 =λ
=λ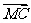 ,λ∈R,
,λ∈R,
则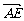 =
=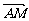 +
+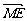 =
=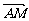 +λ
+λ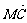 .
.
=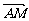 +λ(
+λ(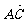 -
-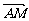 )
)
=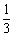
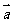 +λ(
+λ(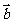 -
-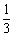
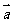 )=(
)=(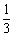 -
-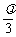 )
)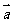 +λ
+λ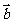 .
.
同理,设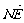 =t
=t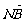 ,t∈R,则
,t∈R,则
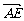 =
=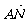 +
+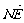 =
=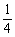
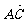 +t
+t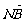 =
=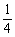
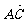 +t(
+t(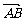 -
-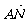 )
)
=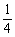
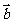 +t(
+t(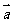 -
-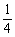
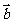 )=(
)=(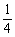 -
-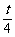 )
)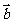 +t
+t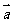 .
.
∴(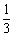 -
-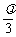 )
)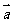 +λ
+λ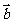 =(
=(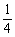 -
-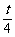 )
)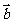 +t
+t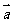 .
.
由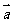 与
与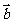 是不共线向量,得
是不共线向量,得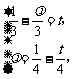 解得
解得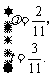
∴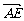 =
=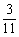 a+
a+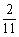 b.
b.
9. 若a、b是两个不共线的非零向量(t∈R).
(1)若a与b起点相同,t为何值时,a、tb、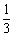 (a+b)三向量的终点在一直线上?
(a+b)三向量的终点在一直线上?
(2)若|a|=|b|且a与b夹角为60°,那么t为何值时,|a-tb|的值最小?
解:(1)设a-tb=m[a-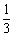 (a+b)](m∈R),
(a+b)](m∈R),
化简得(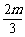 -1)a=(
-1)a=(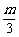 -t)b.
-t)b.
∵a与b不共线,
∴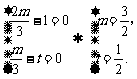
∴t=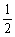 时,a、tb、
时,a、tb、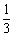 (a+b)的终点在一直线上.
(a+b)的终点在一直线上.
(2)|a-tb|2=(a-tb)2=|a|2+t2|b|2-2t|a||b|cos60°=(1+t2-t)|a|2,
∴t=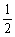 时,|a-tb|有最小值
时,|a-tb|有最小值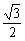 |a|.
|a|.
评述:用两个向量共线的充要条件,可解决平面几何中的平行问题或共线问题.
8.求证:起点相同的三个非零向量 ,
,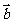 ,3
,3 -2
-2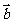 的终点在同一条直线上.
的终点在同一条直线上.
证明:设起点为O,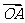 =
= ,
,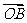 =
=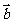 ,
,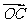 =3
=3 -2
-2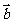 ,
,
则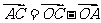 =2(
=2( -
-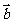 ),
),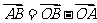 =
=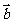 -
- ,
, ,
,
∵ 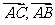 共线且有公共点A,因此,A,B,C三点共线,
共线且有公共点A,因此,A,B,C三点共线,
即向量 ,
,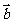 ,3
,3 -2
-2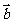 的终点在同一直线上.
的终点在同一直线上.
7.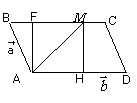 如图:已知在平行四边形ABCD中,AH=HD,BF=MC=
如图:已知在平行四边形ABCD中,AH=HD,BF=MC=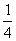 BC,设
BC,设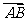 =
= ,
, =
= ,试用
,试用 、
、 分别表示
分别表示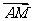 、
、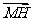 、
、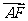
解:∵ 
 ABCD中,BF=MC=
ABCD中,BF=MC=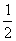 BC,
BC,
∴FM=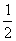 BC=
BC=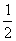 AD=AH ∴FM
AD=AH ∴FM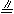
 AH
AH
∴四边形AHMF也是平行四边形,∴AF=HM
又 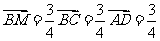
 , 而
, 而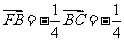

∴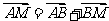 =
=  +
+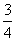
 ,
, 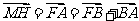 = -
= -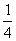
 -
- 
 -(-
-(-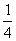
 -
-  ) =
) = 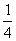
 +
+ 
6.已知(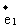 ,
,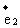 )是平面上一个基底,若
)是平面上一个基底,若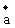 =
=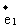 +λ
+λ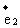 ,
,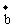 =-2λ
=-2λ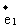 -
-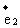 ,若
,若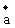 ,
,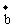 共线,则λ=__________。
共线,则λ=__________。
◆练习简答:1-4.CBCD; 2.易知OC⊥AB,由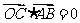 得
得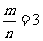 . 3.、、是单位向量,把起点移至原点,终点在单位圆上;方向相同时||最大为3,终点均匀分布在单位圆上时||最小为0. 5. -8; 6.
. 3.、、是单位向量,把起点移至原点,终点在单位圆上;方向相同时||最大为3,终点均匀分布在单位圆上时||最小为0. 5. -8; 6. 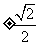
[解答题]
5.设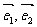 是不共线的向量,已知向量
是不共线的向量,已知向量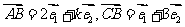 ,
,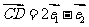 ,若A,B,D三点共线,则k的值等于_________-8
,若A,B,D三点共线,则k的值等于_________-8
4.(2006全国Ⅰ)设平面向量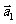 、
、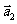 、
、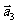 的和
的和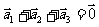 如果向量
如果向量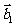 、
、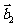 、
、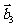 ,满足
,满足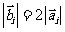 ,且
,且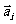 顺时针旋转
顺时针旋转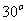 后与
后与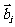 同向,其中
同向,其中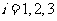 ,则 ( )
,则 ( )
A
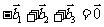 B
B
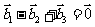
C
 D
D
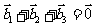
[填空题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com