3．平抛物体运动中的速度变化

水平方向分速度保持v_x＝v₀，竖直方向加速度恒为g，速度v_y＝gt，从抛出点起，每隔Δt时间的速度的矢量关系如图5－3－3所示，这一矢量关系有两个特点：(1)任意时刻的速度水平分量均等于初速度v₀；(2)任意相等时间间隔Δt内的速度改变量均竖直向下，且Δv＝Δv_y＝g·Δt

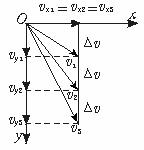
图5－3－3

?

问题全解

平抛运动的飞行时间和水平距离由哪些因素决定？

由于分运动和合运动具有等时性，平抛运动的飞行时间只受下降的距离y的限制，即飞行时间只由竖直分运动决定，与水平分运动无关，只要做平抛运动的物体下降的距离相同，无论水平初速度和质量如何，其飞行时间均相同，且为

t＝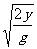

但飞行的水平距离x则由平抛初速度v₀和下降的距离y共同决定，为：

x＝v₀t＝v₀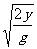

［例1］一架飞机水平匀速地飞行．从飞机上每隔1 s释放一铁球，先后共释放4个．若不计空气阻力，则4个球

A．在空中任何时刻总是排成抛物线，它们的落地点是等间距的

B．在空中任何时刻总是排成抛物线，它们的落地点不是等间距的

C．在空中任何时刻总在飞机正下方排成竖直的直线，它们的落地点是等间距的

D．在空中任何时刻总在飞机正下方排成竖直的直线，它们的落地点是不等间距的

解析：飞机和铁球的水平运动相同(相对地面)．选取飞机为参照物，每个铁球都做自由落体运动，都从飞机上释放，可以判断出4个铁球总在飞机正下方排成竖直的直线，每隔1 s释放1个铁球，故铁球落地点是等间距的．C正确．

点评：如果飞机斜向上匀速飞行，每隔1 s释放1个铁球，则以飞机为参照物，在空中铁球仍在飞机正下方排成竖直的直线．但由于飞机释放铁球的高度不同，铁球落地点是不等间距的．

［例2］如图5－3－4所示，一个小物体由斜面上A点以初速v₀水平抛出，然后落到斜面上B点，已知斜面的倾角为θ，空气阻力可忽略，求物体在运动过程中离斜面的最远距离s．

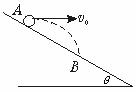
图5－3－4

解析：物体水平抛出，其运动可有多种分解途径，下面我们用两种方法分解．

方法一：

小球的运动可分解成水平方向的匀速直线运动和竖直向下的自由落体运动，如图5－3－5所示．当物体速度与斜面平行时物体距斜面最远．设此过程所经时间t，两方向位移分别是：

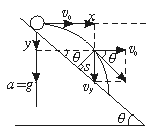
图5－3－5

x＝v₀t　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ①

y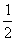＝gt² ②

竖直向下速度：v_y＝gt　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ③

此时由图可知：v_y＝v₀tanθ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ④

根据几何关系(如图5-3-5所示)：

(x－y/tanθ)sinθ＝s　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ⑤

由①②③④⑤得：

s＝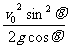

方法二：将小球的运动分解成垂直于斜面方向的运动与沿斜面向下的运动；将重力沿这两方向分解，则物体垂直斜面向上做匀减速直线运动，其初速度v_y0＝v₀sinθ，其加速度a_y＝gcosθ．如图5－3－6所示，当垂直斜面方向速度v_yt＝0时，s最大．由匀变速直线运动公式，得：

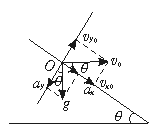
图5－3－6

s＝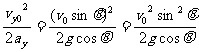

［例3］一小球以初速度v₀水平抛出，落地速度为v_t，阻力不计．求：

①在空中飞行时间；

②抛出点离地面的高度；

③水平射程；

④小球的位移．

解析：

①由做平抛运动的物体在t s末的合速度为：

v_t＝＝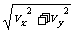

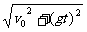
可得t＝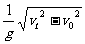

②由竖直方向做自由落体运动，可得：

s_y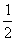＝gt²＝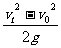

③水平射程：

s_x＝v₀t＝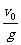

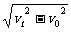
④位移：

s＝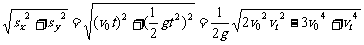

与水平夹角：

tanφ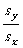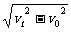＝＝ /2v₀

φ＝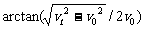

［例4］如图5－3－7所示，由倾角为θ的斜面顶端水平抛出一钢球，落到斜面底端，已知抛出点到落点斜边长L，求抛出的初速度．

图5－3－7

解析：钢球做平抛运动，初速度和时间决定水平位移Lcosθ＝v₀t；飞行时间由下落高度决定，Lsinθ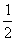＝gt²，可见我们可先求时间再求初速度．

钢球做平抛运动，下落高度：

Lsinθ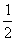＝gt²

飞行时间

t＝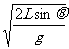

水平飞行距离：

Lcosθ＝v₀t

初速度：

v₀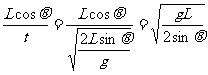＝·cosθ

点评：本题把钢球的运动分解为水平和竖直两个分运动，求解简明．若沿其他直角坐标分解就麻烦多了．

［例5］如图5－3－8所示，一光滑斜面与竖直方向成α角，小球有两种释放方式：第一种方式是在A点松手后沿斜面自由下滑；第二种方式是在A点以速度v₀水平抛出，并落在B点．求：

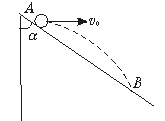
图5－3－8

(1)AB的长度．

(2)两种方式到达B点：下滑的运动时间为t₁，平抛的运动时间为t₂，t₁∶t₂等于多少？

解析：把位移AB向水平方向和竖直方向正交分解，设水平分位移为s，竖直分位移为h，则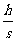＝cotα

(1)平抛运动，水平方向：s＝v₀t₂

竖直方向h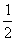＝gt₂²　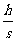＝cotα

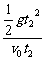＝cotα　所以t₂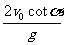＝　s＝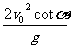

AB＝＝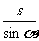

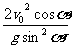
(2)自由下滑，AB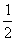＝at₁²

mgcosα＝ma　a＝gcosα

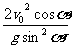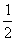＝gcosα·t₁²

t₁²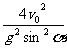＝　t₁＝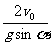

t₁∶t₂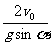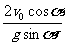＝∶＝1∶cosα

[学习方法指导]

运动叠加法

运动独立性原理又叫运动叠加原理．原理指出：一个运动可以看成是由几个同时进行的各自独立的运动的叠加．这是研究曲线运动的基本方法．中学物理课本中虽然没有明确给出运动独立性原理的文字表述，但教材内容和习题却体现了该原理的思想．我们在研究渡船过河时，把渡船的运动看成是船在静水中的运动和河水的运动的叠加．研究平抛运动时，把它分解为水平方向的匀速直线运动和竖直方向的自由落体运动．研究斜上抛运动时，把它分解为水平方向的匀速直线运动和竖直方向的竖直上抛运动．带电粒子在电场中的偏转也用到运动独立性原理．在物理解题中也常常用到运动独立性原理这一研究运动合成和分解的重要方法．

应用运动独立性原理分析问题，应注意到：(1)各个分运动应是彼此独立的、互不影响的；(2)分运动和合运动具有同时性，各个分运动和合运动是同时进行的．

[知识拓展]

平抛运动的两个重要推论

推论1：做平抛(或类平抛)运动的物体在任一时刻任一位置处，设其速度方向与水平方向的夹角为θ，位移与水平方向的夹角为φ，则tanθ＝2tanφ．

证明：如图5－3－9所示，由平抛运动规律得：

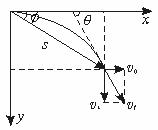
图5－3－9

tanθ＝，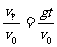

tanφ＝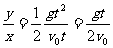

所以tanθ＝2 tanφ．

推论2：做平抛(或类平抛)运动的物体任一时刻的瞬时速度的反向延长线一定通过此时水平位移的中点，如图5－3－10中A点和B点所示．

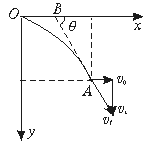
图5－3－10

证明：设平抛物体的初速度为v₀，从原点O到A点的时间为t，A点坐标为(x，y)，B点坐标为(x′，0)，则x＝v₀t

y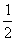＝gt²　v_⊥＝gt，

又tanθ＝，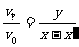

解得x′＝．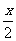

即末状态A点的速度方向反向延长线与x轴的交点B必为A点水平位移的中点．

2．平抛运动的规律

以抛出点为坐标原点，以初速度v₀方向为x正方向，竖直向下为y正方向，如图5－3－1所示．则有：

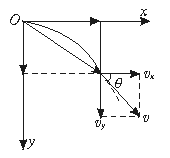
图5－3－1

分速度v_x＝v₀，v_y＝gt

合速度v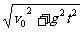＝，tanθ＝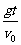

分位移x＝v₀·t，y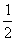＝gt²

合位移s＝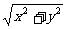

注意：合位移方向与合速度方向不一致．

轨迹：设物体平抛至某点(x，y)，如图5－3－2所示，则轨迹方程为：

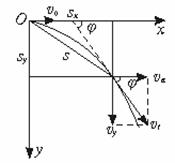
图5－3－2

x＝v₀t，y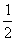＝gt²

消去参数t，得

y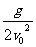＝x²．(抛物线)

1．平抛运动的特点

①受力特点：F_合＝mg，方向竖直向下

②运动特点：

平抛物体的速度方向与受力方向不在一条直线上，故平抛运动是曲线运动．又因为物体受恒力作用，加速度不变，故平抛运动是匀变速运动．

平抛物体的运动是曲线运动的一个特例，其运动特点是具有水平方向初速度和竖直向下的加速度g(只受重力、忽略空气阻力)，由运动的合成与分解知识可知，平抛运动可分解为水平方向的匀速直线运动和竖直方向的自由落体运动．因此，平抛运动问题都可以通过水平方向的分运动和竖直方向的分运动具有等时性的特点进行研究．