
5.若等比数列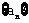 的首项为
的首项为 ,且
,且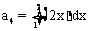 ,则数列
,则数列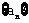 的公比是( )
的公比是( )
A.3 B.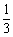 C.27 D.
C.27 D.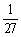
4.如果一个几何体的三视图如图所示(单位长度:cm),
则此几何体的体积是( )
A.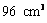 B.
B.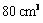
C.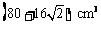 D.
D.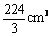
3. 二项式
二项式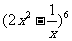 的展开式中,常数项为 ( )
的展开式中,常数项为 ( )
A.30 B.48 C.60 D.120
2.“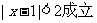 ”是“
”是“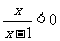 成立”的( )
成立”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
1.复数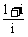 等于( )
等于( )
A.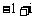 B.
B.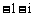 C.
C. D.
D.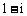
21.解:(1)因为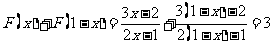 .
………………………2分
.
………………………2分
所以设S= …………(1)
…………(1)
S= .
………(2)
.
………(2)
(1)+(2)得:
 =
= ,所以S=3012. ……………………………………………………5分
,所以S=3012. ……………………………………………………5分
(2)由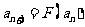 两边同减去1,得
两边同减去1,得 .
………………7分
.
………………7分
所以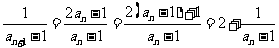 ,
,
所以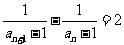 ,
,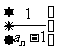 是以2为公差以
是以2为公差以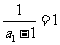 为首项的等差数列,
为首项的等差数列,
所以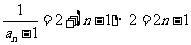
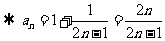 .
…………10分
.
…………10分
(3)因为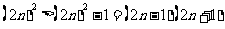
所以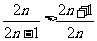
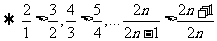 .
……………12分
.
……………12分
所以
>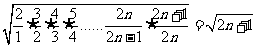 .
…………………………………14分
.
…………………………………14分
20.解:(1)由题意得|PA|=|PB|且|PB|+|PF|=r=8. 故|PA|+|PF|=8>|AF|=4
∴P点轨迹为以A、F为焦点的椭圆.………………………………………………… 3分
设椭圆方程为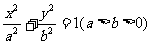
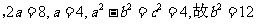
 . …………………………………………………… 6分
. …………………………………………………… 6分
(2)假设存在满足题意的直线L.易知当直线的斜率不存在时, 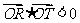 不满足题意.
不满足题意.
故设直线L的斜率为 .
.
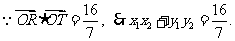 ………………………………………………7分
………………………………………………7分
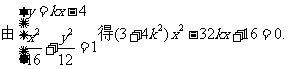 ……………………………………8分
……………………………………8分
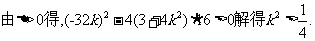 ……………………①.
……………………①.
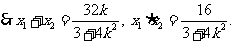 ……………………………………………10分
……………………………………………10分
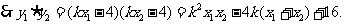 ………………………11分
………………………11分
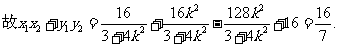
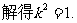 …②.
…②.
由①、②解得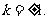
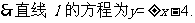 ……………………………………………………13分
……………………………………………………13分
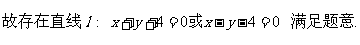 ……………………14分
……………………14分
19.解:(1)直线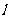 是函数
是函数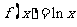 在点
在点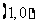 处的切线,故其斜率
处的切线,故其斜率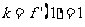 ,
,
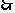 直线
直线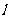 的方程为
的方程为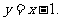 …………………2分
…………………2分
又因为直线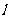 与
与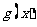 的图象相切,且切于点
的图象相切,且切于点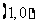 ,
,
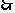
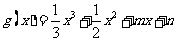 在点
在点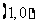 的导函数值为1.
的导函数值为1.
 ,∴
,∴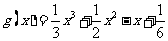 ……6分
……6分
(2)
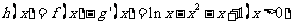 …………………7分
…………………7分
∴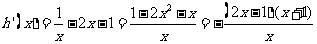 …………………9分
…………………9分
当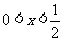 时,
时,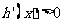 ;当
;当 时,
时,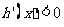 …………………11分
…………………11分
因此,当 时,
时,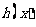 取得极大值,由于极值唯一,
取得极大值,由于极值唯一,
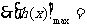
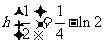 ∴函数
∴函数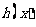 的值域是
的值域是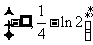 …………14分
…………14分
18.解:(1)因为AC=CB,所以CD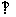 AB,
AB,
又因为ABC-A1B1C1是直三棱柱,所以CD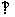 AA1,故CD
AA1,故CD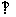 平面ABB1A1 . …………4分
平面ABB1A1 . …………4分
(2)取AC中点E,则DE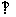 AC,得:DE
AC,得:DE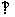 平面ACC1A1,作DH垂直A1C于H,
平面ACC1A1,作DH垂直A1C于H,
则 DHE就是二面角D-A1C-A的平面角………………………………………6分
DHE就是二面角D-A1C-A的平面角………………………………………6分
在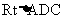 中,DE=
中,DE=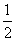 AC=1.EH=
AC=1.EH=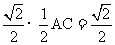
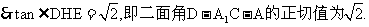 …………………9分
…………………9分
(3)由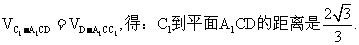 ……………14分
……………14分
17. 解:(1)由已知得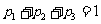 ,∵
,∵ ,∴
,∴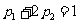 .
……………2分
.
……………2分
∵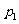 、
、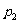 是方程
是方程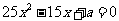 的两个根,∴
的两个根,∴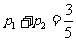 .
……………4分
.
……………4分
∴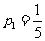 ,
,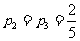 …………………………………………………………6分
…………………………………………………………6分
(2)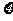 的可能取值为0,100,200,300,400
的可能取值为0,100,200,300,400
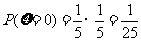 ,
,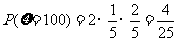 ,
,
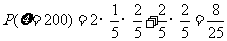 ,
,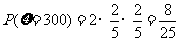 ,
,
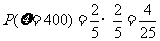 .
………………………………………………………9分
.
………………………………………………………9分
即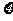 的分布列为:
的分布列为:
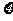 |
0 |
100 |
200 |
300 |
400 |
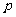 |
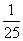 |
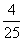 |
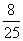 |
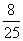 |
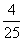 |
故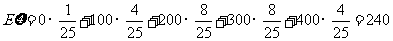 …………12分
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com