
5、 下面给出的文字为开头,以“路”为中心,分别写一段话。每段续写不少于50字。
下面给出的文字为开头,以“路”为中心,分别写一段话。每段续写不少于50字。
①北京的路平直而宽阔
②人生的路漫长而多彩
[答案](一)北京的道路平直而宽阔,无论是长安街还是平安大道,车水马龙,但井然有序,平直的马路让司机开起车来心里踏实,宽阔的马路预示着北京会发展得越来越好。北京的道路平直而宽阔,清晨会有环卫工人为它洗脸,偶尔会有些许雾气滋润它的面庞;中午车来车往真是热闹非凡,在阳光的照射下,它的脸也热了;晚上两旁的路灯就是它佩戴的名贵首饰。(二)人生的路漫长而多彩,就像在天边的大海上航行,有时会风平浪静,行驶顺利;而有时却会是惊涛骇浪,行驶艰难。但只要我们心中的灯塔不熄灭,就能沿着自己的航线继续航行。人生的路漫长而多彩:在阳光中我学会欢笑,在阴云中我学会坚强;在狂风中我抓紧希望,在暴雨中我抓紧理想;当我站在中点回望,我走出了一条属于我的人生之路。
[解析]本题从表面形式看,是考查发散性思维在扩展语句中的运用,但其实质仍然是在某种限制下的写作。题干就包含着如下限制:①以给出的文字为开头,②以“路”为中心,③分别写一段话,④每段续写不少于50字。给出的开头文字分别是:①北京的路平直而宽阔:②人生的路漫长而多彩。前者限定写实,带有北京的地方色彩;后者限定象征,想像人生的缤纷色彩。
4、根据下列两种情景,以“歌声”为重点,分别扩展成一段话。每段话不少于30个字。
情景一:毕业典礼上同学们歌声
情景二:考试前夕我歌声
3、请围绕“节约”这一话题,用“少一点……,多一点……”的句式写三句话,每句话的前后要整齐匀称。
(1)
(2)
(3)
[答案]少一点腹胀浪费,多一点勤俭节约。少一点大手大脚,多一点精打细算。
少一点取用无度,多一点细水长流。
[解析]这一题难度不大,只要设计与“节约”主题有关的三组相对的做法,但一定要注意结构上的要求,力争做到组句子的两个分句字数相等。
2、请以“和谐”为内容写三句话。要求每句话都使用比喻,三句话构成排比。
______________________________________________________________________
______________________________________________________________________
______________________________________________________________________
[答案]和谐是乐手演奏的动人旋律,和谐是画家创作的美丽画卷,和谐是设计师描绘的宏伟蓝图。
[解析]一是注意喻体的选择要准确,因为本体是“和谐”,所以特别要注意喻体的感情色彩。二是要注意排比句的句式要求。
1、请用“银河”、“树影”、“蛙声”等词语写一段情景交融的文字。要求想象合理,语言连贯,不少于40个字。
答:
[答案]夏日的夜晚总喜欢在河边散步,那银盘一般的月亮和疏疏落落但却无比闪亮的星倒映在小河中,一阵微风吹来,那小河真成了波光粼粼的“银河”了。河岸上婆娑的树影和河中热闹的蛙声,更是荡漾起心中无数的喜悦。
[解析]要注意根据三个主题词设计一个合理的情境,尤其要注意不能一味过于客观地写景,而是要做到“景”中有“情”。
130. 已知等腰DABC中,AC = BC = 2, ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
解析:解:设点P在底面上的射影为O,连OB、OC,
则OC是PC在平面ABC内的射影,
∴ PCO是PC与面ABC所成的角。
PCO是PC与面ABC所成的角。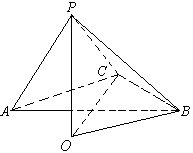
∵ PA = PB = PC,
∴点P在底面的射影是DABC的外心,
注意到DABC为钝角三角形,
∴点O在DABC的外部,
∵AC = BC,O是DABC的外心,
∴OC⊥AB
在DOBC中,OC = OB,  OCB = 60°,
OCB = 60°,
∴DOBC为等边三角形,∴OC = 2
在RtDPOC中,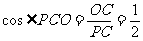
∴ PCO = 60° 。
PCO = 60° 。
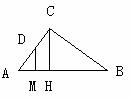
129. 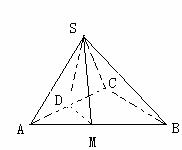 如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=
如图平面SAC⊥平面ACB,ΔSAC是边长为4的等边三角形,ΔACB为直角三角形,∠ACB=90°,BC=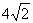 ,求二面角S-AB-C的余弦值。
,求二面角S-AB-C的余弦值。
解析:先作出二面角的平面角。由面面垂直可得线面垂直,作SD⊥平面ACB,然后利用三垂线定理作出二面角的平面角
解:过S点作SD⊥AC于D,过D作DM⊥AB于M,连SM
∵平面SAC⊥平面ACB
∴SD⊥平面ACB
∴SM⊥AB
 又∵DM⊥AB
又∵DM⊥AB
∴∠DMS为二面角S-AB-C的平面角
在ΔSAC中SD=4×
在ΔACB中过C作CH⊥AB于H
∵AC=4,BC=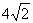
∴AB=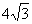
∵S=1/2AB·CH=1/2AC·BC
∴CH=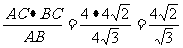
∵DM∥CH且AD=DC
∴DM=1/2CH=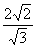
∵SD⊥平面ACB DMÌ平面ACB
∴SD⊥DM
在RTΔSDM中
SM=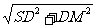
=
=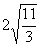
∴cos∠DMS=
=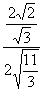
=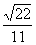
128. 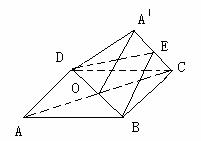 正方形ABCD中,以对角线BD为折线,把ΔABD折起,使二面角Aˊ-BD-C 为60°,求二面角B-AˊC-D的余弦值
正方形ABCD中,以对角线BD为折线,把ΔABD折起,使二面角Aˊ-BD-C 为60°,求二面角B-AˊC-D的余弦值
解析:要求二面角B-AˊC-D的余弦值,先作出二面角的平面角,抓住图形中AˊB=BC,AˊD=DC的关系,采用定义法作出平面角∠BED(E为AC的中点)然后利用余弦定理求解
解:连BD、AC交于O点
则AˊO⊥BD,CO⊥BD
∴∠AˊOC为二面角Aˊ-BD-C的平面角
∴∠AˊOC=60°
设正方形ABCD的边长为a
∵A′O=OC=1/2AC=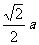
∠A′OC=60°
∴ΔA′OC为正三角形则A′C=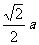
取A′C的中点,连DE、BE
∵A′B=BC
∴BE⊥A′C
同理DE⊥A′C
∴∠DEB为二面角B-A′C-D的平面角在ΔBA′C中
BE=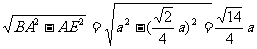
同理DE=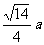
在ΔBED中,BD=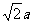
∴ cos∠BED=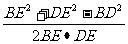
=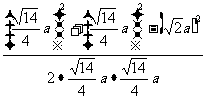
=--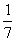
∴二面角B-A′C-D的余弦值为-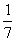
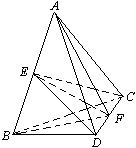
127. 已知空间四边形ABCD中,AB = BC =CD= AD = BD = AC, E、F分别为AB、CD的中点,
(1)求证:EF 为AB和CD的公垂线
(2)求异面直线AB和CD的距离
解析:构造等腰三角形证明EF 与AB、CD垂直,然后在等腰三角形中求EF
解;①连接BD和AC,AF和BF,DE和CE
设四边形的边长为a
∵ AD = CD = AC = a
∴ △ABC为正三角形
∵ DF = FC
∴ AF ^ DC 且AF =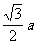
同理 BF = 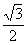 A
A
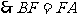
即△ AFB为等腰三角形
在△ AFB中,
∵ AE = BE
∴ FE ^ AB
同理在 △ DEC中
EF ^ DC
∴ EF为异面直线AB和CD的公垂线
②在 △ AFB中
∵ EF ^ AB且 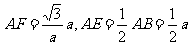
∴ 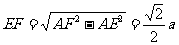
∵ 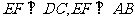
∴ EF为异面直线AB和CD的距离
∴ AB和CD的距离为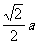
126.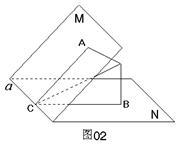 在60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求P点到直线a的距离.
在60°的二面角M-a-N内有一点P,P到平面M、平面N的距离分别为1和2,求P点到直线a的距离.
解析:本题涉及点到平面的距离,点到直线的距离,二面角的平面角等概念,图中都没有表示,按怎样的顺序先后作出相应的图形是解决本题的关键.可以有不同的作法,下面仅以一个作法为例,说明这些概念的特点,分别作PA⊥M,M是垂足,PB⊥N,N是垂足,先作了两条垂线,找出P点到两个平面的距离,其余概念要通过推理得出:于是PA、PB确定平面α,设α∩M=AC,α∩N=BC,c∈a.由于PA⊥M,则PA⊥a,同理PB⊥a,因此a⊥平面α,得a⊥PC.这样,∠ACB是二面角的平面角,PC是P点到直线a的距离,下面只要在四边形ACBP内,利用平面几何的知识在△PAB中求出AB,再在△ABC中利用正弦定理求外接圆直径2R=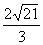 ,即为P点到直线a的距离,为
,即为P点到直线a的距离,为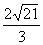 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com