
4.换元法
例4.求函数 的值域
的值域
解:设
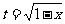 则
t
则
t 0 x=1-
0 x=1-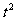
代入得
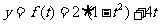
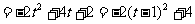
∵t 0 ∴y
0 ∴y 4
4
3.判别式法(△法):
判别式法一般用于分式函数,其分子或分母只能为二次式,解题中要注意二次项系数是否为0的讨论
例3.求函数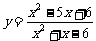 的值域
的值域
方法一:去分母得 (y-1)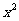 +(y+5)x-6y-6=0 ①
+(y+5)x-6y-6=0 ①
当
y¹1时 ∵xÎR ∴△=(y+5)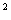 +4(y-1)×6(y+1)
+4(y-1)×6(y+1) 0
0
由此得 (5y+1)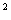
 0
0
检验
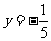 时
时 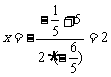 (代入①求根)
(代入①求根)
∵2 Ï 定义域 { x| x¹2且 x¹3} ∴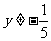
再检验 y=1 代入①求得 x=2 ∴y¹1
综上所述,函数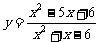 的值域为
{ y| y¹1且 y¹
的值域为
{ y| y¹1且 y¹ }
}
方法二:把已知函数化为函数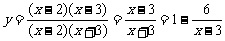 (x¹2)
(x¹2)
由此可得 y¹1
∵
x=2时 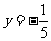 即
即 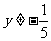
∴函数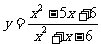 的值域为
{ y| y¹1且 y¹
的值域为
{ y| y¹1且 y¹ }
}
说明:此法是利用方程思想来处理函数问题,一般称判别式法. 判别式法一般用于分式函数,其分子或分母只能为二次式.解题中要注意二次项系数是否为0的讨论.
2.二次函数比区间上的值域(最值):
例2 求下列函数的最大值、最小值与值域:
①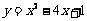 ;
;
②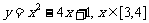 ;
;
③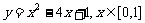 ;
④
;
④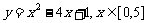 ;
;
解:∵ ,∴顶点为(2,-3),顶点横坐标为2.
,∴顶点为(2,-3),顶点横坐标为2.
①∵抛物线的开口向上,函数的定义域R,
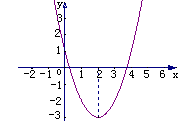 ∴x=2时,ymin=-3 ,无最大值;函数的值域是{y|y
∴x=2时,ymin=-3 ,无最大值;函数的值域是{y|y -3
}.
-3
}.
②∵顶点横坐标2 [3,4],
[3,4],
当x=3时,y= -2;x=4时,y=1;
∴在[3,4]上, =-2,
=-2,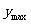 =1;值域为[-2,1].
=1;值域为[-2,1].
③∵顶点横坐标2 [0,1],当x=0时,y=1;x=1时,y=-2,
[0,1],当x=0时,y=1;x=1时,y=-2,
∴在[0,1]上, =-2,
=-2,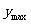 =1;值域为[-2,1].
=1;值域为[-2,1].
④∵顶点横坐标2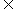 [0,5],当x=0时,y=1;x=2时,y=-3, x=5时,y=6,
[0,5],当x=0时,y=1;x=2时,y=-3, x=5时,y=6,
∴在[0,1]上, =-3,
=-3,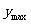 =6;值域为[-3,6].
=6;值域为[-3,6].
注:对于二次函数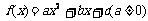 ,
,
⑴若定义域为R时,
①当a>0时,则当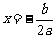 时,其最小值
时,其最小值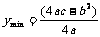 ;
;
②当a<0时,则当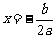 时,其最大值
时,其最大值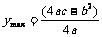 .
.
⑵若定义域为x [a,b],则应首先判定其顶点横坐标x0是否属于区间[a,b].
[a,b],则应首先判定其顶点横坐标x0是否属于区间[a,b].
①若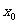
 [a,b],则
[a,b],则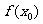 是函数的最小值(a>0)时或最大值(a<0)时,再比较
是函数的最小值(a>0)时或最大值(a<0)时,再比较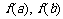 的大小决定函数的最大(小)值.
的大小决定函数的最大(小)值.
②若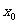
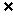 [a,b],则[a,b]是在
[a,b],则[a,b]是在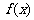 的单调区间内,只需比较
的单调区间内,只需比较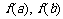 的大小即可决定函数的最大(小)值.
的大小即可决定函数的最大(小)值.
注:①若给定区间不是闭区间,则可能得不到最大(小)值;
②当顶点横坐标是字母时,则应根据其对应区间特别是区间两端点的位置关系进行讨论.
1.直接法:利用常见函数的值域来求
一次函数y=ax+b(a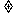 0)的定义域为R,值域为R;
0)的定义域为R,值域为R;
反比例函数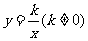 的定义域为{x|x
的定义域为{x|x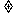 0},值域为{y|y
0},值域为{y|y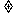 0};
0};
二次函数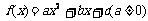 的定义域为R,
的定义域为R,
当a>0时,值域为{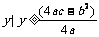 };当a<0时,值域为{
};当a<0时,值域为{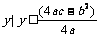 }.
}.
例1.求下列函数的值域
①
y=3x+2(-1 x
x 1) ②
1) ②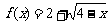
③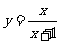 ④
④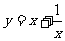
解:①∵-1 x
x 1,∴-3
1,∴-3 3x
3x 3,
3,
∴-1 3x+2
3x+2 5,即-1
5,即-1 y
y 5,∴值域是[-1,5]
5,∴值域是[-1,5]
②∵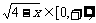 ∴
∴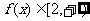
即函数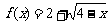 的值域是 { y| y
的值域是 { y| y 2}
2}
③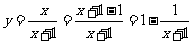
∵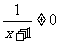 ∴
∴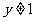
即函数的值域是 { y| yÎR且y¹1}(此法亦称分离常数法)
④当x>0,∴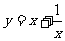 =
=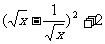
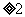 ,
,
当x<0时,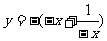 =-
=-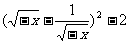

∴值域是 [2,+
[2,+ ).(此法也称为配方法)
).(此法也称为配方法)
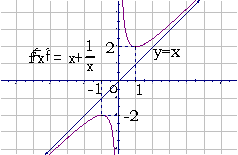 函数
函数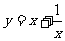 的图像为:
的图像为:
函数的三要素是:定义域、值域和定义域到值域的对应法则;对应法则是函数的核心(它规定了x和y之间的某种关系),定义域是函数的重要组成部分(对应法则相同而定义域不同的映射就是两个不同的函数);定义域和对应法则一经确定,值域就随之确定
函数的表示方法⑴解析法优点:一是简明、全面地概括了变量间的关系;二是可以通过解析式求出任意一个自变量的值所对应的函数值.中学阶段研究的函数主要是用解析法表示的函数.
⑵列表法优点:不需要计算就可以直接看出与自变量的值相对应的函数值.
⑶图象法:优点:能直观形象地表示出自变量的变化,相应的函数值变化的趋势,这样使得我们可以通过图象来研究函数的某些性质.
前面我们已经学习了函数定义域的求法和函数的表示法,今天我们来学习求函数值域的几种常见方法
20、 利用所给词语写一段话,介绍“征集全民健身口号”活动的结果,要求语意完整,句子通顺,字数在50-60之间。
利用所给词语写一段话,介绍“征集全民健身口号”活动的结果,要求语意完整,句子通顺,字数在50-60之间。
来源广 一个月 入选口号 千余条 “我运动,我快乐”
答:
。
[答案]全民健身口号征集活动在一个月里收到应征口号千余条,稿件来源广,参与人数多,经过评审,最终入选口号为“我运动,我快乐”。
[解析]解答时要利用所给词语,语意完整,扣住主题“征集全民健身口号”,同时注意话题前后保持一致,语言连贯流畅,语言应富有激情,有文采,有感染力。符合字数要求。
19、以“溪”、“海”和“潭”为意象写一段文字,要求表达某种感悟,至少运用一种修辞手法,不超过60字。(5分)
18、根据下面的新闻材料,拟一条一句话新闻(不超过15字)。
淮河、巢湖一直是国家水污染防治的重点流域。安徽省根据今年年初国家淮河流域水污染防治考核组提出的评估意见,采取措施进一步开展淮河、巢湖流域的水污染防治工作。据了解,今年,安徽将加快重点环保工程建设,要求已列入淮河、巢湖流域“十一五”计划而未开工的城镇污水处理厂项目,4月底以前必须全面开工建设,年底前实现两流域所有审、县全部建成管网配套的污水处理厂的目标。同时要求各级地方政府的相关部门积极协调,加强环境监管,提高环境监察、监测和统计能力,加大对环境违法行为的处罚力度,鼓励环保建设中的制度创新、技术研发和信贷倾斜。
[答案]①淮河、巢湖的治污步伐加快。 ②淮河、巢湖治污提速。 ③安徽强化淮河、巢湖水污染防治。
[解析]这是个老题型,考生应该很熟练。所给答案要点要求又不高。
17、请根据所给材料,把下列两个语句补充完整。要求对材料内容分别进行概括。(5分)
地震、风灾、冰灾、海啸等灾难的发生,是不以人类的意志为转移的;但是人类可以在灾难面前万众一心、积极应对,而不是畏惧退缩、怨天尤人。
我们不能选择 ,但我们能够选择
[答案]示例:要不要灾难 对待灾难的态度
[解析]压缩时要注意上下文的连贯。第一空对应原文分号前的内容,第二空对应分号后的内容。
16、用一句话概括下面材料的主要信息。不超过16个字。
2008年北京奥运会的举办不仅能为北京吸引更多的游客,还将为亚洲其他国家和地区吸引更多的游客。据调查,有74%的游客考虑在观看完北京奥运会后去日本、新加坡、泰国和中国香港旅游。
[答案]举例:北京奥运会将惠及亚洲的旅游业。
[解析]语段一共两个层次,第一句讲的是“北京奥运会为亚洲吸引更多的游客”;第二句讲的是“游客会顺便到亚洲其他地方旅游”。把两者合起来概括就是答案。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com