
2、排列数与组合数都是计算完成事件方法个数的公式,排列数是研究排列(既取又排)个数的公式,组合数是研究组合(只取不排)个数的公式,是否有序是它们之间的本质区别。
排列数公式: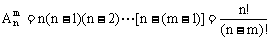 ,当m=n时,
,当m=n时,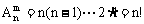 ,其中m,n∈N+,m≤n,规定0!=1
,其中m,n∈N+,m≤n,规定0!=1
组合数公式: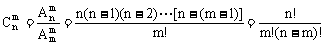
组合数性质: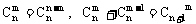 ,规定
,规定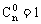 ,其中m,n∈N+,m≤n
,其中m,n∈N+,m≤n
1、分类计数原理和分步计数原理是排列组合的基础和核心,既可用来推导排列数、组合数公式,也可用来直接解题。它们的共同点都是把一个事件分成若干个分事件来进行计算。只不过利用分类计算原理时,每一种方法都可能独立完成事件;如需连续若干步才能完成的则是分步。利用分类计数原理,重在分“类”,类与类之间具有独立性和并列性;利用分步计数原理,重在分步;步与步之间具有相依性和连续性。比较复杂的问题,常先分类再分步。
3、理解随机事件的概率,会求等可能事件的概率,能用加法公式和乘法公式求互斥事件和相互独立事件同时发生的概率。
2、掌握二项式定理,会用展开式通项求有关展开式的问题。
1、排列数、组合数的计算、化简、证明等;会解排列、组合应用题,掌握常见应用题的处理思路。
《排列、组合、二项式定理和概率》
补充:求函数y=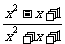 值域
值域
解:∵ ,
,
∴函数的定义域R,原式可化为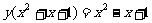 ,
,
整理得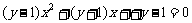 ,
,
若y=1,即2x=0,则x=0;
若y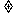 1,∵
1,∵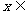 R,即有
R,即有
 0,
0,
∴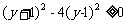 ,解得
,解得 且
y
且
y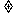 1.
1.
综上:函数是值域是{y| }.
}.
求函数值域的基本方法(直接法、换元法、判别式法);二次函数值域(最值)或二次函数在某一给定区间上的值域(最值)的求法.
1 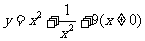 ;
;
解:∵x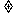 0,
0,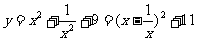 ,∴y
,∴y 11.
11.
另外,此题利用基本不等式解更简捷: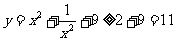
2 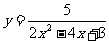
∵2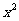 -4x+3>0恒成立(为什么?),
-4x+3>0恒成立(为什么?),
∴函数的定义域为R,
∴原函数可化为2y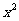 -4yx+3y-5=0,由判别式
-4yx+3y-5=0,由判别式
 0,
0,
即16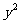 -4×2y(3y-5)=-8
-4×2y(3y-5)=-8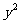 +40y
+40y 0(y
0(y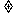 0),
0),
解得0 y
y 5,又∵y
5,又∵y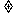 0,
∴0<y
0,
∴0<y 5.
5.
注意:利用判别式法要考察两端点的值是否可以取到.
3 求函数的值域
①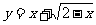 ;
②
;
②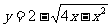
解:①令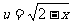
 0,则
0,则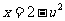 ,
,
原式可化为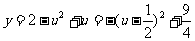 ,
,
∵u 0,∴y
0,∴y
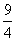 ,∴函数的值域是(-
,∴函数的值域是(- ,
,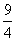 ].
].
②解:令
t=4x-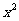
 0 得 0
0 得 0 x
x 4
4
在此区间内 (4x-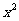 )
)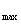 =4
,(4x-
=4
,(4x-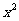 )
)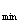 =0
=0
∴函数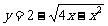 的值域是{ y| 0
的值域是{ y| 0 y
y 2}
2}
5.分段函数
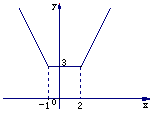 例5.求函数y=|x+1|+|x-2|的值域.
例5.求函数y=|x+1|+|x-2|的值域.
解法1:将函数化为分段函数形式: ,画出它的图象(下图),由图象可知,函数的值域是{y|y
,画出它的图象(下图),由图象可知,函数的值域是{y|y 3}.
3}.
解法2:∵函数y=|x+1|+|x-2|表示数轴上的动点x到两定点-1,2的距离之和,∴易见y的最小值是3,∴函数的值域是[3,+ ]. 如图
]. 如图



两法均采用“数形结合”,利用几何性质求解,称为几何法或图象法.
说明:以上是求函数值域常用的一些方法(观察法、配方法、判别式法、图象法、换元法等),随着知识的不断学习和经验的不断积累,还有如不等式法、三角代换法等.有的题可以用多种方法求解,有的题用某种方法求解比较简捷,同学们要通过不断实践,熟悉和掌握各种解法,并在解题中尽量采用简捷解法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com