
3.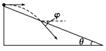 (2008·全国卷Ⅰ)如图3所示,一物体自倾角为θ的固定斜面
(2008·全国卷Ⅰ)如图3所示,一物体自倾角为θ的固定斜面
顶端沿水平方向抛出后落在斜面上.物体与斜面接触时速度
与水平方向的夹角φ满足 ( ) 图3
A.tanφ=sinθ B.tanφ=cosθ
C.tanφ=tanθ D.tanφ=2tanθ
解析:物体的竖直分速度与水平分速度之比为tanφ=,物体的竖直分位移与水平
分位移之比为tanθ=,故tanφ=2tanθ,D正确.
答案:D
2.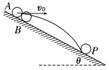 如图2所示,A、B为两个挨得很近的小球,并列放于光滑斜
如图2所示,A、B为两个挨得很近的小球,并列放于光滑斜
面上,斜面足够长,在释放B球的同时,将A球以某一速度
v0水平抛出,当A球落于斜面上的P点时,B球的位置位于
( ) 图2
A.P点以下
B.P点以上
C.P点
D.由于v0未知,故无法确定
解析:设A球落到P点的时间为tA,AP的竖直位移为y;B球滑到P点的时间为tB,
BP的竖直位移也为y,则:tA= ,tB= = >tA(θ为斜面倾
角).故B项正确.
答案:B
1.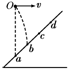 如图1所示,斜面上有a、b、c、d四个点,ab=bc=cd.从a点正
如图1所示,斜面上有a、b、c、d四个点,ab=bc=cd.从a点正
上方的O点以速度v水平抛出一个小球,它落在斜面上的b点.若
小球从O点以速度2v水平抛出,不计空气阻力,则它落在斜面上的
( ) 图1
A.b与c之间某一点
B.c点
C.c与d之间某一点
D.d点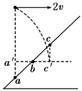
解析:如右图所示,作c点在竖直方向的投影点c′,则以2v抛
出的小球应落在c′点(如果没有斜面),所以碰上斜面的话,就应
在b与c之间.
答案:A
(三) 解答题
20、某天的课程表要排入政治、语文、数学、物理、体育、美术共6节课,如果第1节不排体育,最后1节不排数学,那么共有多少种不同的排课表的方法。
21、有甲、乙、丙三位老师,分到6个班上课:
(1)每人上2个班课,有多少种分法?
(2)甲、乙都上1个班课,丙上4个班课,有多少种分法?
(3)2人各上1个班课,1个人上4个班课,有多少种分法?
22、在x(1-x)k+x2(1+2x)8+x3(1+3x)12的展开式中,含x4的系数是144,求k的值并求出含x2项的系数等于多少?
23、某气象站天气预报的准确率为80%,求:
(1)5次预报中恰有4次准确的概率;
(2)5次预报中至少有4次准确的概率(结果保留2位有效数字)。
24、有6个房间安排4个旅游者住,每人可以进住任一房间,且进住房间是等可能的,试求下列事件的概率:
(1)事件A:指定的4个房间各有1人;
(2)事件B:恰有4个房间中各有1人;
(3)事件C:指定的某个房间中有2人;
(4)事件D:第1号房间有1人,第2号房间有3人。
25、有甲、乙两批种子,发芽率分别为0.8,0.7,从两批种子中各取1粒,求:
(1)2粒种子都能发芽的概率;
(2)至少有1粒种子发芽的概率;
(3)恰好有1粒种子发芽的概率。
26、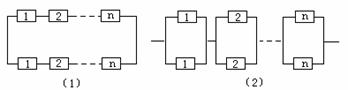 如图构成系统的每个元件的可靠性为r(0<r,r<1),且各个元件能否正常工作是相互独立的,试求图中两种系统的可靠性。
如图构成系统的每个元件的可靠性为r(0<r,r<1),且各个元件能否正常工作是相互独立的,试求图中两种系统的可靠性。
(二) 填空题
15、空间12个点,其中5个点共面,此外无任何4个点共面,这12个点最多可决定_________个不同的平面。
16、(4+2x+x2)(2-x)7展开式中x5的系数为________。
17、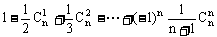 =__________。
=__________。
18、有1个数字难题,在半小时内,甲能解决它的概率是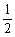 ,乙能解决它的概率是
,乙能解决它的概率是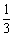 ,两人试图独立地在半小时内解决它,则:两人都未解决的概率为__________;问题得到解决的概率为__________。
,两人试图独立地在半小时内解决它,则:两人都未解决的概率为__________;问题得到解决的概率为__________。
19、一次考试出了10个选择题,每道题有4个可供选择的答案,其中1个是正确的,3个是错误的,某学生只知道5个题的正确答案,对其他5个题全靠猜回答,那么这个学生卷面上正确答案不少于7个题的概率是_________。
(一) 选择题
1、某一排共12个座位,现甲、乙、丙三人按如下要求入座,每人左右两旁都有空座位,且三人的顺序是甲必须在另两人之间,则不同的座法共有
A、60种 B、112种 C、242种 D、672种
2、某同学从6门课中选学2门,其中有2门课上课时间有冲突,另有2门不允许同时选学,则该同学可选学的方法总数有
A、8种 B、13种 C、12种 D、9种
3、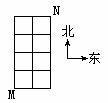 如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有
如图,在某城市中,M、N两地间有整齐的道路网,若规定只能向东或向北两个方向沿图中的矩形的边前进,则从M到N不同的走法共有
A、13种 B、15种 C、25种 D、10种
4、将n个不同的小球放入n个不同的盒子里,恰好有一个空盒的放法种数是
A、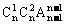 B、
B、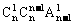 C、
C、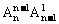 D、
D、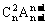
5、若(1-2x)9=a0+a1x+a2x2+…+a8x8+a9x9,则a1+a2+…+a8的值为
A、-1 B、-2 C、-512 D、510
6、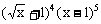 展开式中,x4的系数为
展开式中,x4的系数为
A、-40 B、10 C、40 D、45
7、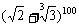 的展开式中无理项的个数是
的展开式中无理项的个数是
A、84 B、85 C、86 D、87
8、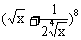 的展开式中系数最大的项是
的展开式中系数最大的项是
A、第3项 B、第4项 C、第2或第3项 D、第3或第4项
9、掷三颗骰子(各面上分别标以数字1到6的均匀正方体玩具),恰有一颗骰子出1点或6点的概率是
A、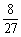 B、
B、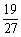 C、
C、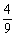 D、
D、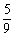
10、一工人看管三台机床,在一小时内甲、乙、丙三台机床需要工人照看的概率分别是0.9,0.8和0.85,那么在一小时中至少有一台机床不需要照看的概率是
A、0.003 B、0.612 C、0.388 D、0.027
11、在4次独立重复试验中,随机事件A恰好发生1次的概率不大于其恰好发生两次的概率,则事件A在一次试验中发生的概率P的取值范围是
A、[0.4,1] B、(0,0.4] C、(0,0.6] D、[0.6,1)
12、一批零件10个,其中有8个合格品,2个次品,每次任取一个零件装配机器,若第一次取得合格品的概率是P1,第二次取得合格品的概率是P2,则
A、P1>P2 B、P1=P2 C、P1<P2 D、P1=2P2
13、一个学生通过某种英语听力测试的概率是1/2,他连续测试n次,要保证他至少有一次通过的概率大于0.9,那么n的最小值为
A、3 B、4 C、5 D、6
14、甲、乙两人投篮命中的概率分别为p、q,他们各投两次,若p=1/2,且甲比乙投中次数多的概率恰好等于7/36,则q的值为
A、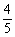 B、
B、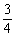 C、
C、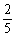 D、
D、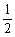
例1、用n种不同颜色为下列两块广告牌着色(如图),要求在①,②,③,④个区域中相邻(有公共边界)的区域不用同一种颜色。
(1)若n=6,为甲着色时共有多少种不同方法?
(2)若为乙着色时共有120种不同方法,求n。
解:完成着色这件事,共分四个步骤,可依次考虑为①、②、③、④着色时各自的方法数,再由乘法原理确定决的着色方法数。因此
(1)为①着色有6种方法,为②着色有5种方法,为③着色有4种方法,为④着色也只有4种方法。
∴ 共有着色方法6×5×4×4=480种
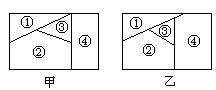 (2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
(2)与①的区别在于与④相邻的区域由两块变成了三块,同理,不同的着色方法数是n(n-1)(n-2)(n-3)
由n(n-1)(n-2)(n-3)=120
∴ (n2-3n)(n2-3n+2)-120=0
即(n2-3n)2+2(n2-3n)-12×10=0
∴ n2-3n-10=0
∴ n=5
例2、计算下列各题:
(1)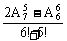
(2)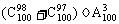
(3)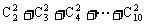
解:(1)原式=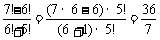
(2)原式=
(3)原式=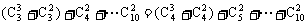
=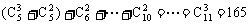
例3、按以下要求分配6本不同的书,各有几种分法?
(1)平均分给甲、乙、丙三人,每人2本;
(2)平均分成三份,每份2本;
(3)甲、乙、丙三人一人得1本,一人得2本,一人得3本;
(4)分成三份,一份1本,一份2本,一份3本;
(5)甲、乙、丙三人中,一人得4本,另二人每人得1本;
(6)分成三份,一份4本,另两份每份1本;
(7)甲得1本,乙得1本,丙得4本(均只要求列式)
解:(1)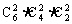 ;
;
(2)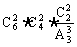
(3)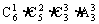
(4)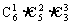
(5)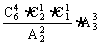
(6)
(7)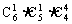
评注:有关排列组合混合题常常是先组合再排列。
例4、四面体的顶点和各棱中点共有10个点,在其中取4个不共面的点,不同的取法共有( )
A、150种 B、147种 C、144种 D、141种
解:从10个点中任取4个点有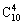 种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有
种取法,其中4点共面的情况有三类。第一类,取出的4个点位于四面体的同一个面内,有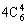 种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有
种;第二类,取任一条棱上的3个点及该棱对棱的中点,这4点共面,有6种;第三类,由中位线构成的平行四边形(其两组对边分别平行于四面体相对的两条棱),它的4个点共面,有3种。以上三种情况不合要求应减掉,所以不同的取法共有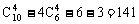 (种)
(种)
例5、求(4+2x+x2)(2-x)7的展开式中x5的系数。
解:(4+2x+x2)(2-x)7=(8-x3)(x-2)6
=(8-x3)[(x6-2C61x5+(-2)2C62x4+(-2)3C63x3+(-2)4C64x2+…]
∴ 含x5的项为-2×8×C61·x5-(-2)4C64x5=-336x5
∴ x5的系数为-336
例6、已知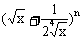 的展开式前三项中的x的系数成等差数列。
的展开式前三项中的x的系数成等差数列。
(1)求展开式里所有的x的有理项;
(2)求展开式里系数最大的项。
解:(1)∵ 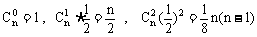
由题设可知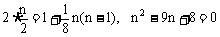
解得n=8或n=1(舍去)
当n=8时,通项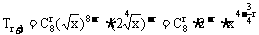
据题意,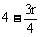 必为整数,从而可知r必为4的倍数,而0≤r≤8
必为整数,从而可知r必为4的倍数,而0≤r≤8
∴
r=0,4,8,故x的有理项为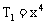 ,
,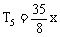 ,
,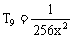
(3)设第r+1项的系数tr+1最大,显然tr+1>0,故有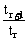 ≥1且
≥1且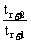 ≤1
≤1
∵
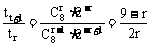
由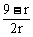 ≥1得r≤3
≥1得r≤3
又∵
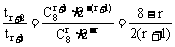
由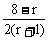 ≤1得:r≥2
≤1得:r≥2
∴
r=2或r=3所求项为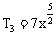 和
和
例7、设a>1,n∈N,且n≥2,求证: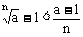
证明:设 ,则(x+1)n=a
,则(x+1)n=a
欲证原不等式,即证nx<(x+1)n-1,其中x>0
∵
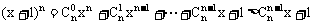
即(x+1)n>nx+1,原不等式成立。
评注:由于(a+b)n的展开式共有n+1项,故可通过对某些项的取舍来达到近似计算或证明不等式的目的。
例8、盒中有6只灯泡,其中2只次品,4只正品,有放回地从中任取两次,每次取一只,试求下列事件的概率:
(1)取到的2只都是次品;
(2)取到的2只中正品、次品各一只;
(3)取到的2只中至少有一只正品。
解:从6只灯泡中有放回地任取两只,共有62=36种不同取法
(1)取到的2只都是次品情况为22=4种,因而所求概率为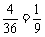
(2)由于取到的2只中正品、次品各一只有两种可能:第一次取到正品,第二次取到次品;及第一次取到次品,第二次取到正品。因而所求概率为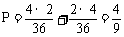
(3)由于“取到的两只中至少有一只正品”是事件“取到的两只都是次品”的对立事件,因而所求概率为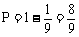
例9、甲、乙两人独立地破译1个密码,他们能译出的密码的概率分别为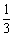 和
和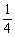 ,求:
,求:
(1)恰有1人译出的密码的概率;
(2)至多1人译出的密码的概率;
(3)若达到译出的密码的概率为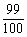 ,至少需要多少个乙这样的人。
,至少需要多少个乙这样的人。
解:记“甲译出密码”为事件A,“甲译不出密码”这事件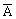 ;记“乙译出密码”为事件B,“乙译不出密码”为事件
;记“乙译出密码”为事件B,“乙译不出密码”为事件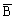 ;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
;“两人都译出密码”为事件C,“两人都译不出密码”为事件D;“恰有1人译出密码”为事件E;“至多1人译出密码”为事件F。
(1)“恰有1人译出密码”是包括2种情况:一种是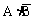 ,另一种是
,另一种是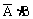 。这两种情况不能同时发生,是互斥的。
。这两种情况不能同时发生,是互斥的。
∴
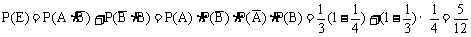
(2)“至多1人译出密码”包括两种情况:“2人都译不出密码”或“恰有1人译出密码”,即事件D+E,且事件D、E是互斥的
∴
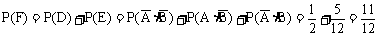
(3)n个乙这样的人都译不出密码的概率为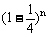 ,根据题意得:
,根据题意得: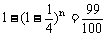
解得:n=16
例10、某数学家有两盒火柴,每盒都有n根火柴,每次用火柴时他在两盒中任取一盒并从中抽出一根,求他发现用完一盒时另一盒还有r根(1≤r≤n)的概率。
解析:由题意知:数学家共用了2n-r根火柴,其中n根取自一盒火柴,n-r根取自另一盒火柴。
由于数学家取火柴时,每次他在两盒中任取一盒并从中抽取一根,故他用完的那一盒取出火柴的概率是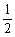 ,他不从此盒中取出一根火柴的概率也是
,他不从此盒中取出一根火柴的概率也是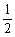 。
。
由于所取的2n-r根火柴,有n根取自用完的那一盒的概率为:
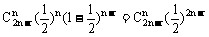
5、概率
(1)概率是频率的近似值,两者是不同概念
(2)等可能事件中概率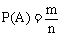 ,P(A)∈[0,1]
,P(A)∈[0,1]
(3)互斥事件A,B中有一个发生的概率:加法公式P(A+B)=P(A)+P(B)
特例: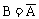 时,
时,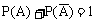 ,即对立事件的概率和为1
,即对立事件的概率和为1
(4)相互独立事件A,B同时发生的概率P(A·B)=P(A)P(B)
(5)事件A在n次独立重复试验中恰好发生k次的概率Pn(k)=CnkPk(1-P)n-k,其中P为事件A在一次试验中发生的概率,此式为二项式[(1-P)+P]n展开的第k+1项
4、二项式定理
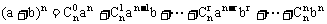
通项公式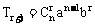 ,r=0,1,2,…,n
,r=0,1,2,…,n
二项式系数的性质:
(1)对称性,在展开式中,与首末两端“等距离”的两个二项式系数相等,即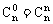 ,
,
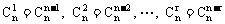 ;
;
(2)增减性与最大值:在二项式展开式中,二项式系数先增后减,且在中间取得最大值,当n是偶数时,中间一项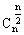 最大;当n是奇数时,中间两项
最大;当n是奇数时,中间两项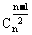 ,
,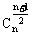 相等,且为最大值;
相等,且为最大值;
(3)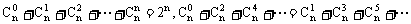
3、处理排列组合应用题的规律
(1)两种思路:直接法,间接法
(2)两种途径:元素分析法,位置分析法
(3)对排列组合的混合题,一般先选再排,即先组合再排列。弄清要完成什么样的事件是前提
(4)基本题型及方法:捆绑法,插空法,错位法,分组分配法,均匀分组法,逆向思考法等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com