
4. (2005浙江).已知向量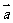 ≠
≠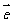 ,|
,|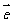 |=1,对任意t∈R,恒有|
|=1,对任意t∈R,恒有|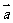 -t
-t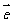 |≥|
|≥|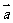 -
-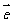 |,则
( )
|,则
( )
A. 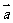 ⊥
⊥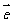 B.
B. 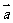 ⊥(
⊥(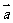 -
-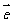 ) C.
) C.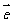 ⊥(
⊥(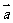 -
-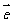 ) D. (
) D. (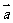 +
+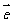 )⊥(
)⊥(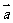 -
-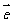 )
)
3.(2006陕西) 已知非零向量与满足(+)·=0且·= , 则△ABC为 ( )
A 三边均不相等的三角形 B 直角三角形
C 等腰非等边三角形 D 等边三角形
2.(2005江西).已知向量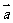 =(1,2),
=(1,2),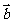 =(-2,-4),|
=(-2,-4),|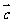 |=
|= 若
若 则
则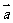 与
与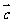 的夹角为
( )
的夹角为
( )
A.30° B.60° C.120° D.150°
1.(2006北京)若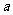 与
与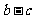 都是非零向量,则“
都是非零向量,则“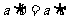 ”是“
”是“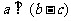 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件 ( )
(C)充分必要条件 (D)既不充分也不必要条件
5.向量数量积的性质:
(1)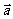 ⊥
⊥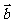
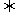
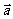 ·
·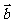 =O
=O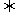
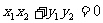
(2)当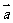 与
与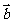 同向时,
同向时,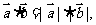 当
当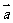 与
与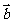 反向时,
反向时,
一般地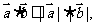 特别地:
特别地: --向量运算与模的转化。
--向量运算与模的转化。
(3)求夹角:cos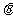 =
=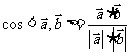 =
=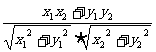
若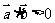 则
则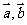 夹角为锐角或00;
夹角为锐角或00;
若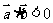 则
则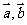 夹角为钝角或1800.
夹角为钝角或1800.
(4)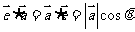 。
。
4.两个向量的数量积的坐标运算:
已知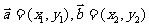 ,则
,则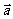 ·
·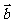 =
=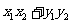
3.平面向量数量积的运算律:①交换律成立: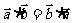
②对实数的结合律成立: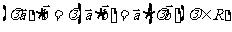
③分配律成立: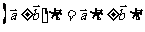
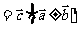
④乘法公式成立:
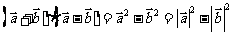 ;
;
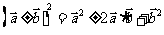
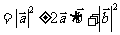
特别注意:(1)结合律不成立: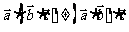 ;
;
(2)消去律不成立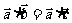
 不能得到
不能得到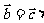
(3)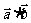 =0
=0 不能得到
不能得到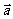 =
=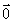 或
或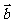 =
=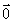
1两个向量的数量积:
(1)设两个非零向量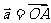 与
与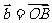 ,称∠AOB=
,称∠AOB=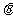 为向量
为向量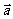 与
与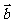 的夹角, (00≤θ≤1800),当非零向量
的夹角, (00≤θ≤1800),当非零向量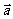 与
与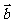 同方向时,θ=00,当
同方向时,θ=00,当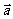 与
与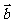 反方向时θ=1800,
反方向时θ=1800,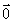 与其它非零向量不谈夹角问题
与其它非零向量不谈夹角问题
(2)数量积的定义: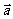 ·
·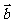 =︱
=︱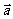 ︱·︱
︱·︱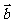 ︱cos
︱cos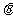 , 叫做
, 叫做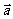 与
与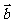 的数量积; 规定
的数量积; 规定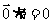 ,其中︱
,其中︱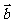 ︱cos
︱cos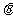 ∈R,叫向量
∈R,叫向量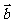 在
在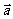 方向上的投影.
方向上的投影.
2.数量积的几何意义: 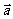 ·
·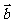 等于
等于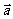 的长度与
的长度与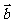 在
在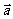 方向上的投影的乘积.
方向上的投影的乘积.
2.了解用平面向量的数量积可以处理有关长度、角度和垂直的问题.
1.掌握平面向量的数量积及其几何意义; 掌握向量垂直的条件;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com