
1. (2006湖北1)已知向量 a=(
a=(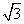 ,1),b是不平行于x轴的单位向量,且a
,1),b是不平行于x轴的单位向量,且a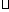 b=
b=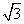 ,则b=
( )
,则b=
( )
A.(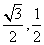 ) B.(
) B.(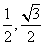 ) C.(
) C.(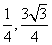 ) D.(1,0)
) D.(1,0)
3.向量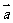 与
与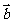 的夹角:(1)当a与
的夹角:(1)当a与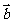 必有公共起点,否则要平移;(2)0°≤〈
必有公共起点,否则要平移;(2)0°≤〈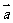 ,
,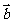 〉≤180°;(3)cos〈
〉≤180°;(3)cos〈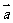 ,
,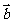 〉=
〉=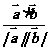 =
=
同步练习 5.3平面向量的数量积
[选择题]
2.用数量积处理向量垂直问题,向量的长度、角度问题.
1.平面向量的数量积、几何意义及坐标表示;
[例1]已知向量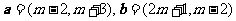 的夹角为钝角,求m的取值范围.
的夹角为钝角,求m的取值范围.
解: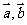 夹角为钝角则
夹角为钝角则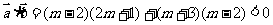
解得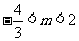
又当 时,
时,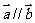 ,
,
∴m的取值范围是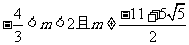
[例2]已知两单位向量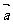 与
与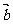 的夹角为
的夹角为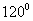 ,若
,若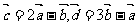 ,试求
,试求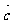 与
与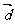 的夹角。
的夹角。
解:由题意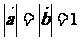 ,且
,且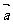 与
与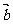 的夹角为
的夹角为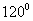
所以,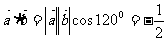
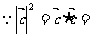


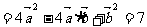 ,
,
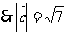 ,同理可得
,同理可得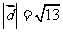
而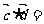
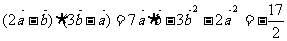 ,设
,设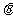 为
为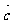 与
与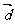 的夹角,则
的夹角,则

[例3]已知向量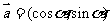 ,
, ,且
,且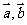 满足关系
满足关系
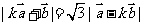 ,(k为正实数).
,(k为正实数).
(1)求证: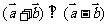 ;
;
(2)求将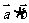 表示为k的函数f(k).
表示为k的函数f(k).
(3)求函数f(k)的最小值及取最小值时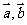 的夹角θ.
的夹角θ.
解(1)证明: 
(2)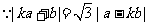
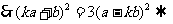
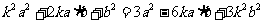

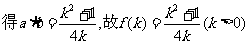
(3)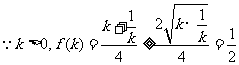
当且仅当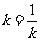 即k=1时,故f(x)的最小值是
即k=1时,故f(x)的最小值是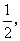
此时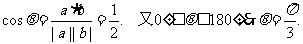
 [例4]如图,四边形MNPQ是⊙C的内接梯形,C是圆心,C在MN上,向量
[例4]如图,四边形MNPQ是⊙C的内接梯形,C是圆心,C在MN上,向量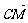 与
与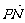 的夹角为120°,
的夹角为120°,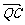 ·
·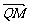 =2.
=2.
(1)求⊙C的方程;
(2)求以M、N为焦点且过点P、Q的椭圆的方程.
剖析:需先建立直角坐标系,为了使所求方程简单,需以C为原点,MN所在直线为x轴,求⊙C的方程时,只要求半径即可,求椭圆的方程时,只需求a、b即可.
解:(1)以MN所在直线为x轴,C为原点,建立直角坐标系xOy.
∵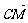 与
与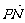 的夹角为120°,故∠QCM=60°.于是△QCM为正三角形,∠CQM=60°.
的夹角为120°,故∠QCM=60°.于是△QCM为正三角形,∠CQM=60°.
又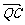 ·
·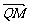 =2,即|
=2,即|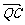 ||
||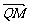 |cos∠CQM=2,于是r=|
|cos∠CQM=2,于是r=|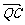 |=2.
|=2.
故⊙C的方程为x2+y2=4.
(2)依题意2c=4,2a=|QN|+|QM|,
而|QN|=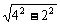 =2
=2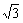 ,|QM|=2,
,|QM|=2,
于是a=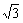 +1,b2=a2-c2=2
+1,b2=a2-c2=2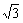 .
.
∴所求椭圆的方程为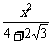 +
+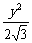 =1.
=1.
[研讨.欣赏]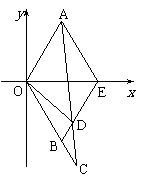 如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点.
如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点.
⑴用t表示向量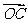 和
和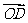 的坐标;
的坐标;
⑵求向量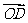 和
和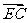 的夹角的大小.
的夹角的大小.
解:⑴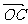 =((t+1),-(t+1)),
=((t+1),-(t+1)),
∵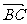 =t
=t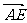 ,∴
,∴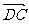 =t
=t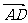 ,
,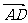 =
=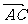 ,又
,又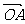 =(,),
=(,),
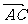 =
=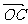 -
-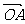 =(t,-(t+2));∴
=(t,-(t+2));∴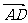 =(,-),
=(,-),
∴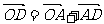 =(,-)
=(,-)
⑵∵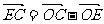 =(,-),
=(,-),
∴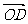 ·
·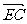 =·+·=
=·+·=
又∵|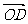 |·|
|·|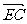 |=
|=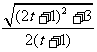 ·=
·=
∴cos<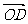 ,
,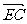 >==,∴向量
>==,∴向量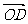 与
与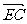 的夹角为60°
的夹角为60°
4.利用图形分析, 5.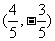 或
或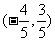 ; 6.
; 6.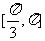 ; 7.
; 7. 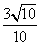 ; 8.1.
; 8.1.
8.(2006天津)设函数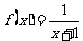 ,点
,点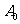 表示坐标原点,点
表示坐标原点,点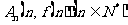 ,若向量
,若向量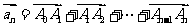 ,
,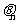 是
是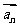 与
与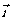 的夹角,(其中
的夹角,(其中 ),设
),设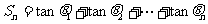 ,则
,则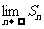 = .
= .
简答:1-4.CCDC;
7.(2006天津)设向量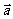 与
与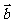 的夹角为
的夹角为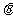 ,且
,且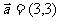 ,
,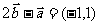 ,则
,则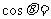 __________.
__________.
6. 已知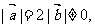 且关于
且关于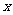 的方程
的方程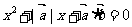 有实根, 则
有实根, 则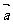 与
与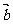 的夹角的取值范围是________
的夹角的取值范围是________
5.与向量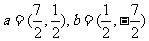 的夹角相等,且模为1的向量=______
的夹角相等,且模为1的向量=______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com