
本章主要内容是极限和导数的概念与运算法则,以及导数在几何、函数等方面的应用。
(1)极限是本章也是整个微积分的基础概念,它包括数列极限和函数极限,它们都是是在无限变化过程中(n→∞,x→∞或x→x0)的变化趋势,这一共同点决定了两类极限有类似的运算性质;如果两个数列(或函数)有极限,那么它们的和、差、积、商的极限分别等于这两个数列(或函数)的极限的和、差、积、商(作为除数的数列或函数的极限不能为0)。其原因在于无穷数列{an}是定义域为N+的特殊函数an=f(n),数列的极限 是函数极限
是函数极限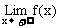 =A的特例。
=A的特例。
极限概念及运算性质决定了确定极限的两种方法:一是利用数形结合思想,从量变中认识质变的数学思想方法,即极限方法。利用极限的方法求出了变速直线运动的瞬时速度与曲线上某点的切线方程,并从中抽象出函数的导数概念。导数是一种特殊的函数极限,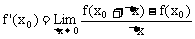 ,x0变化时,f’(x0)就是导函数,二是利用极限的运算法则,可推导出最常用的导数公式与运算法则:c’=0(c为常数),(xn)’=nxn-1(n∈N+),[f(x)±g(x)]’=f’(x)±g’(x),[cf(x)]’=cf’(x),进一步可以求出所有多项式函数的导数。
,x0变化时,f’(x0)就是导函数,二是利用极限的运算法则,可推导出最常用的导数公式与运算法则:c’=0(c为常数),(xn)’=nxn-1(n∈N+),[f(x)±g(x)]’=f’(x)±g’(x),[cf(x)]’=cf’(x),进一步可以求出所有多项式函数的导数。
 (2)导数f’(x)是函数平均变化率
(2)导数f’(x)是函数平均变化率 的极限
的极限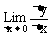 ,瞬时速度、切线斜率、经济学中的边际成本都与平均变化率有关,因而导数有广泛的作用。
,瞬时速度、切线斜率、经济学中的边际成本都与平均变化率有关,因而导数有广泛的作用。
(3)本章思想方法
①极限思想:在变化中求不变,在运动中求静止的思想;
②数形结合思想,如用导数的几何意义及用导数求单调性、极值等。
极限与导数复习
2.(2008年江苏18)
在平面直角坐标系 中,记二次函数
中,记二次函数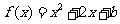 (
(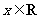 )与两坐标轴有
)与两坐标轴有
三个交点.经过三个交点的圆记为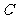 .
.
(1)求实数b的取值范围;
(2)求圆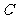 的方程;
的方程;
(3)问圆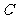 是否经过定点(其坐标与
是否经过定点(其坐标与 的无关)?请证明你的结论.
的无关)?请证明你的结论.
解:本小题主要考查二次函数图象与性质、圆的方程的求法.
(Ⅰ)令 =0,得抛物线与
=0,得抛物线与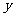 轴交点是(0,b);
轴交点是(0,b);
令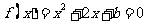 ,由题意b≠0 且Δ>0,解得b<1 且b≠0.
,由题意b≠0 且Δ>0,解得b<1 且b≠0.
(Ⅱ)设所求圆的一般方程为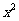

令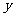 =0 得
=0 得 这与
这与 =0 是同一个方程,故D=2,F=
=0 是同一个方程,故D=2,F= .
.
令 =0 得
=0 得 =0,此方程有一个根为b,代入得出E=―b―1.
=0,此方程有一个根为b,代入得出E=―b―1.
所以圆C 的方程为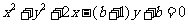 .
.
(Ⅲ)圆C 必过定点,证明如下:
假设圆C过定点 ,将该点的坐标代入圆C的方程,
,将该点的坐标代入圆C的方程,
并变形为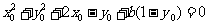 (*)
(*)
为使(*)式对所有满足 的
的 都成立,必须有
都成立,必须有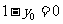 ,结合(*)式得
,结合(*)式得
 ,解得
,解得
经检验知,点 均在圆C上,因此圆C 过定点。
均在圆C上,因此圆C 过定点。
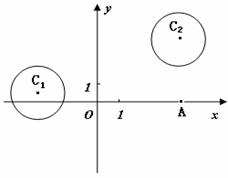
1.(2009年江苏18)(本小题满分16分)
在平面直角坐标系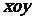 中,已知圆
中,已知圆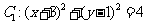 和圆
和圆
 .
.
 (1)若直线
(1)若直线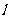 过点
过点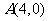 ,且被圆
,且被圆 截得的弦长为
截得的弦长为 ,求直线
,求直线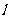 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线 和
和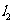 ,它们分别与圆
,它们分别与圆 和圆
和圆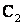 相交,且直线
相交,且直线 被圆
被圆 截得的弦长与直线
截得的弦长与直线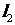 被圆
被圆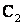 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
[解析] 本小题主要考查直线与圆的方程、点到直线的距离公式,考查数学运算求解能力、综合分析问题的能力。满分16分。
(1)设直线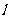 的方程为:
的方程为: ,即
,即
由垂径定理,得:圆心 到直线
到直线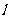 的距离
的距离 ,
,
结合点到直线距离公式,得: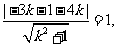
化简得:
求直线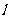 的方程为:
的方程为: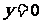 或
或 ,即
,即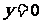 或
或
(2) 设点P坐标为 ,直线
,直线 、
、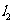 的方程分别为:
的方程分别为:
 ,即:
,即:
因为直线 被圆
被圆 截得的弦长与直线
截得的弦长与直线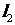 被圆
被圆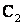 截得的弦长相等,两圆半径相等。由垂径定理,得::圆心
截得的弦长相等,两圆半径相等。由垂径定理,得::圆心 到直线
到直线 与
与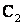 直线
直线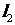 的距离相等。
的距离相等。
故有: ,
,
化简得: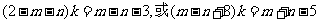
关于 的方程有无穷多解,有:
的方程有无穷多解,有: 解之得:点P坐标为
解之得:点P坐标为 或
或 。
。
12.(2007年山东理15)与直线 和曲线
和曲线 都相切的半径最小的圆的标准方程是_________.
都相切的半径最小的圆的标准方程是_________.
[答案]:.  [分析]:曲线化为
[分析]:曲线化为 ,其圆心到直线
,其圆心到直线 的距离为
的距离为 所求的最小圆的圆心在直线
所求的最小圆的圆心在直线 上,其到直线的距离为
上,其到直线的距离为 ,圆心坐标为
,圆心坐标为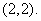 标准方程为
标准方程为 。
。
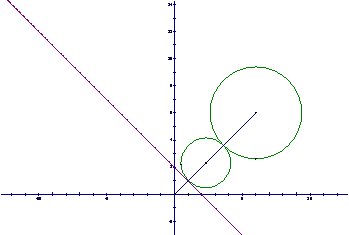
11.(2008年上海理15)如图,在平面直角坐标系中, 是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、P’(x’,y’)满足x≤x’ 且y≥y’,则称P优于P’,如果
是一个与x轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、P’(x’,y’)满足x≤x’ 且y≥y’,则称P优于P’,如果 中的点Q满足:不存在
中的点Q满足:不存在 中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
中的其它点优于Q,那么所有这样的点Q组成的集合是劣弧( )
 A.
B. C. D.
A.
B. C. D.
[答案] [解析]依题意,在点Q组成的集合中任取一点,过
[解析]依题意,在点Q组成的集合中任取一点,过
该点分别作平行于两坐标轴的直线,构成的
左上方区域(权且称为“第二象限”)与点
Q组成的集合无公共元素,这样点Q组成的
集合才为所求. 检验得:D.
10.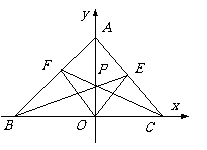 (2008年江苏9)如图,在平面直角坐标系
(2008年江苏9)如图,在平面直角坐标系 中,设三角形
中,设三角形 的顶点分别为
的顶点分别为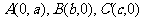 ,点
,点 在线段AO上的一点(异于端点),这里
在线段AO上的一点(异于端点),这里 均为非零实数,设直线
均为非零实数,设直线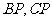 分别与边
分别与边 交于点
交于点 ,某同学已正确求得直线
,某同学已正确求得直线 的方程为
的方程为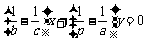 ,请你完成直线
,请你完成直线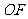 的方程: ( ▲ )
的方程: ( ▲ )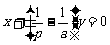 。
。
[解析]本小题考查直线方程的求法.画草图,由对称性可猜想填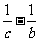 .事实上,由截距式可得直线AB:
.事实上,由截距式可得直线AB: ,直线CP:
,直线CP: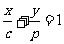 ,两式相减得
,两式相减得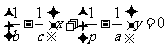 ,显然直线AB与CP 的交点F 满足此方程,又原点O 也满足此方程,故为所求直线OF
的方程.[答案]
,显然直线AB与CP 的交点F 满足此方程,又原点O 也满足此方程,故为所求直线OF
的方程.[答案]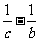
9.(2008年广东理11)经过圆 的圆心
的圆心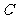 ,且与直线
,且与直线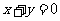 垂直的直线
垂直的直线
方程是 .
[解析]易知点C为 ,而直线与
,而直线与 垂直,我们设待求的直线的方程为
垂直,我们设待求的直线的方程为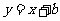 ,将点C的坐标代入马上就能求出参数
,将点C的坐标代入马上就能求出参数 的值为
的值为 ,故待求的直线的方程为
,故待求的直线的方程为 。
。
8.(2009年天津理14)若圆 与圆
与圆 (a>0)的公共弦的长为
(a>0)的公共弦的长为 ,则
,则 ___________
___________
解析:由知 的半径为
的半径为 ,由图可知
,由图可知
解之得
7.(2009年天津理13) 设直线 的参数方程为
的参数方程为 (t为参数),直线
(t为参数),直线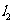 的方程为y=3x+4则
的方程为y=3x+4则 与
与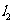 的距离为_______
的距离为_______
[考点定位]本小题考查参数方程化为普通方程、两条平行线间的距离,基础题。
解析:由题直线 的普通方程为
的普通方程为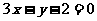 ,故它与与
,故它与与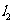 的距离为
的距离为 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com