
5. (2010·茂名模拟)如图5所示,在倾角α=30°的光滑斜面上,
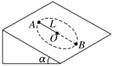
(2010·茂名模拟)如图5所示,在倾角α=30°的光滑斜面上,
有一根长为L=0.8 m的细绳,一端固定在O点,另一端系一
质量为m=0.2 kg的小球,小球沿斜面做圆周运动.若要小球
能通过最高点A,则小球在最低点B的最小速度是 ( ) 图5
A.2 m/s B.2 m/s
C.2 m/s D.2 m/s
解析:通过A点的最小速度为vA==2 m/s,则根据机械能守恒定律得:mvB2
=mvA2+mgL,解得vB=2 m/s,即C选项正确.
答案:C
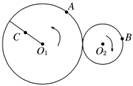
4.如图4所示,靠摩擦传动做匀速转动的大、小两轮接触
面互不打滑,大轮半径是小轮半径的2倍.A、B分别为
大、小轮边缘上的点,C为大轮上一条半径的中点.则
( ) 图4
A.两轮转动的角速度相等
B.大轮转动的角速度是小轮的2倍
C.质点加速度aA=2aB
D.质点加速度aB=4aC
解析:两轮不打滑,边缘质点线速度大小相等,vA=vB,而rA=2rB,故ωA=ωB,
A、B错误;由an=得==,C错误;由an=ω2r得==2,则=4,D
正确.
答案:D
3. (2010·临沂模拟)如图3所示,某同学用硬塑料管和一个质量为m的铁
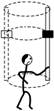
(2010·临沂模拟)如图3所示,某同学用硬塑料管和一个质量为m的铁
质螺丝帽研究匀速圆周运动,将螺丝帽套在塑料管上,手握塑料管使其
保持竖直并沿水平方向做半径为r的匀速圆周运动,则只要运动角速度
大小合适,螺丝帽恰好不下滑.假设螺丝帽与塑料管间的动摩擦因数为
μ,认为最大静摩擦力近似等于滑动摩擦力.则在该同学手转动塑料管 图3
使螺丝帽恰好不下滑时,下述分析正确的是 ( )
A.螺丝帽受的重力与最大静摩擦力平衡
B.螺丝帽受到杆的弹力方向水平向外,背离圆心
C.此时手转动塑料管的角速度ω=
D.若杆的转动加快,螺丝帽有可能相对杆发生运动
解析:由于螺丝帽做圆周运动过程中恰好不下滑,则竖直方向上重力与最大静摩擦
力平衡,杆对螺丝帽的弹力提供其做匀速圆周运动的向心力,有mg=Ff=μFN=
μmω2r,得ω= ,选项A正确、B、C错误;杆的转动速度增大时,杆对螺丝
帽的弹力增大,最大静摩擦力也增大,螺丝帽不可能相对杆发生运动,故选项D
错误.
 答案:A
答案:A
2.如图2所示,OO′为竖直轴,MN为固定在OO′上的水
平光滑杆,有两个质量相同的金属球A、B套在水平杆上,
AC和BC为抗拉能力相同的两根细线,C端固定在转轴
OO′上.当绳拉直时,A、B两球转动半径之比恒为2∶1,
当转轴的角速度逐渐增大时 ( ) 图2
A.AC先断 B.BC先断
C.两线同时断 D.不能确定哪根线先断
解析:对A球进行受力分析,A球受重力、支持力、拉力FA三个力作用,拉力的分
力提供A球做圆周运动的向心力,得:
水平方向FAcosα=mrAω2,
同理,对B球:FBcosβ=mrBω2,
由几何关系,可知cosα=,cosβ=.
所以:===.
由于AC>BC,所以FA>FB,即绳AC先断.
答案:A
1.如图1所示,天车下吊着两个质量都是m的工件A和B,系A
的吊绳较短,系B的吊绳较长.若天车运动到P处突然停止,则
两吊绳所受的拉力FA和FB的大小关系为 ( )
A.FA>FB B.FA<FB 图1
C.FA=FB=mg D.FA=FB>mg
解析:天车运动到P处突然停止后,A、B各以天车上的悬点为圆心做圆周运动,线
速度相同而半径不同,由F-mg=m,得:F=mg+m,因为m相等,v相等,
而LA<LB,所以FA>FB,A选项正确.
 答案:A
答案:A
(三) 解答题
17、(10分)已知无穷数列{an}存在极限,且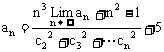 ,求
,求 。
。
18、(12分)设函数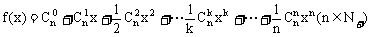 ,求
,求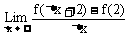 的值。
的值。
19、(12分)已知曲线C1:y=ax2上点P处的切线为1,曲线C2:y=bx3上点A(1,b)处的切线为2,且1⊥2,垂足M(2,2),求a、b的值及点P的坐标。
20、(12分)求函数f(x)=p2x2(1-x)p(p∈N+),在[0,1]内的最大值。
21、(14分)证明双曲线xy=a2上任意一点的切线与两坐标轴组成的三角形面积等于常数。
22、(14分)已知曲线S:y=x3+px2+qx的图象与x轴相切于不同于原点的一点,又函数有极小值-4,求p、q的值。
(二) 填空题(每小题4分,共16分)
13、若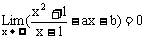 ,则a=______,b=______。
,则a=______,b=______。
14、已知偶函数f(x)在(0,+∞)内满足f’(x)>0,f(0)>0,则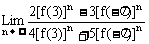 =__________。
=__________。
15、抛物线y=x2上点切线和直线3x-y+1=0的交角为450,则点P坐标为__________。
16、两个和为48的正整数,第一个数的立方与第二个数的平方之和最小,则这两个正整数分别为__________。
(一) 选择题(每小题5分,共60分)
1、 等差数列中,若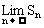 存在,则这样的数列
存在,则这样的数列
A、 有且仅有一个 B、有无数多个 C、有一个或无穷多个 D、不存在
2、 已知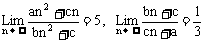 ,如果bc≠0,那么
,如果bc≠0,那么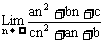 =
=
A、 15
B、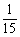 C、
C、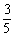 D、
D、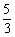
3、 若r为实常数,则集合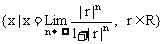
A、恰有一个元素 B、恰有两个元素 C、恰有三个元素 D、无数多个元素
4、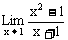 的值
的值
A、2 B、1 C、0 D、不存在
5、函数y=(x2-1)3+1在x=-1处
A、 有极大值 B、无极值 C、有极小值 D、无法确定极值情况
6、 f(x)=ax3+3x2+2,f’(-1)=4,则a=
A、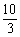 B、
B、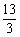 C、
C、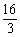 D、
D、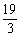
7、过抛物线y=x2上的点M(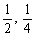 )的切线的倾斜角是
)的切线的倾斜角是
A、300 B、450 C、600 D、900
8、函数f(x)=x3-6bx+3b在(0,1)内有极小值,则实数b的取值范围是
A、 A、(0,1) B、(-∞,1) C、(0,+∞) D、(0,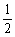 )
)
9、 函数y=x3-3x+3在[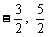 ]上的最小值是
]上的最小值是
A、 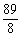 B、1
C、
B、1
C、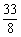 D、5
D、5
10、若f(x)=x3+ax2+bx+c,且f(0)=0为函数的极值,则
A、c≠0 B、当a>0时,f(0)为极大值
C、b=0 D、当a<0时,f(0)为极小值
11、已知函数y=2x3+ax2+36x-24在x=2处有极值,则该函数的一个递增区间是
A、(2,3) B、(3,+∞) C、(2,+∞) D、(-∞,3)
12、方程6x5-15x4+10x3+1=0的实数解的集合中
A、至少有2个元素 B、至少有3个元素 C、至多有1个元素 D、恰好有5个元素
2、当a<0时,f(x)在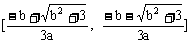 上单调递增;在(-∞,
上单调递增;在(-∞,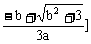 ,
,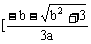 ,+∞)上单调递减。
,+∞)上单调递减。
例6、用总长为14.8m的钢条制作一个长方体容器的框架,如果所制容器的底面的一边比另一边长0.5m,那么为多少时容器的容积最大?并求出它的最大容积?
解题思路分析:
设容器底面短边长为xm,另一边长为(x+0.5)m,高为(3.2-2x)m
∵ 3.2-2x>0,x>0
∴ 0<x<1.6
设容器的容积为ym3
y=x(x+0.5)(3.2-2x)
∴ y=-2x3+2.2x2+1.6x
∴ y’=-6x2+4.4x+1.6
令y’=0得x=1,x=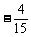 (舍)
(舍)
∵ y在(0,1.6)内只有一个驻点x=1,而x过小或过大时,y值很小
∴ 当x=1时,ymax=1.8,此时高为1.2
例1、 求下列极限
(1) (2)
(2)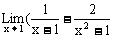 )
)
解题思路分析:
(1)因分子及分母的次数随n增大而增加,故不能利用运算性质。先求和化简。
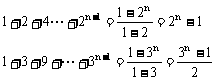
∴
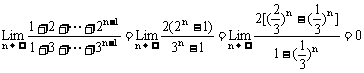
(2)当x→1时,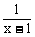 及
及 均无意义,应约去因式x-1
均无意义,应约去因式x-1
∵
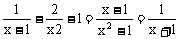
∴
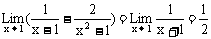
说明:函数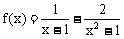 在x=1 无定义,但与
在x=1 无定义,但与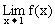 存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则
存在无关。一般地有下列结论:如果f(x)=x0处无定义,g(x)在x=x0处有定义并存在极限,且当x≠x0时,f(x)=g(x),则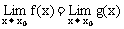 。
。
例2、设函数y=ax3+bx2+cx+d的图象与y轴交点为P,且曲线在P点处的切线方程为12x-y-4=0,若函数在x=2处取得极值0,试确定函数的解析式。
解题思路分析:
P(0,d)
∵ 曲线在点P处切线为12x-y-4=0
∴ x=0时,y=d
∴ d=-4
∵ y’=3ax2+2bx+c
∴ y’|x=0=c
又切线斜率k=12
∴ c=12
又函数在x=2处取得极值0
∴
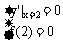
∴

∴
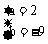
∴ 函数解析式y=2x3-9x2+12x-4
例3、偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P(0,1),且在x=1处的切线方程为y=x-2
(1)求y=f(x)的解析式;
(2)求y=f(x)的极大(小)值。
解题思路分析:
∵ f(x)是偶函数
∴ b=d=0
又图象过P(0,1)
∴ e=1
此时f(x)=ax4+cx2+1
∵ y’=4ax3+2cx
∴ y’|x=1=4a+2c=1 ①
又切点(1,-1)在曲线上
∴ a+c+1=-1 ②
由①②得: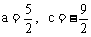
∴
f(x)=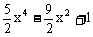
(2)f’(x)=10x3-9x=0
∴
x=0,x=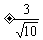
列表可得: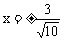 时,f(x)极小=
时,f(x)极小=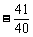
x=0时,f(x)极大=1
例4、曲线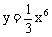 上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
上哪一点的法线在y轴上截距最小?(法线是指过曲线上一点与以此点为切点的切线垂直的直线)
解题思路分析:
在曲线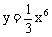 上任取一点(x0,y0),则过该点切线的斜率为k=2x05
上任取一点(x0,y0),则过该点切线的斜率为k=2x05
∴
法线的斜率为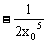
∴
法线方程y-y0=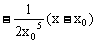
令x=0,使法线在y轴上的截距
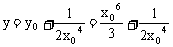
∴
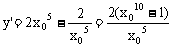
令y’=0,得x0=±1
当x0<-1时,y’<0,∴y单调递减
当-1<x0<0时,y’>0,∴y单调递增
当0<x0<1时,y’<0,∴y单调减小
当x0>1时,y’>0,则y单递增
∴
当x0=±1时,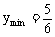 ,此时点(±1,
,此时点(±1,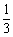 )
)
例5、研究函数f(x)=ax3+bx2-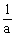 x+1的单调性(a≠0)
x+1的单调性(a≠0)
解题思路分析:
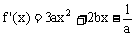
1、a>0时,由f’(x)>0得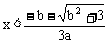 或
或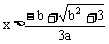
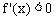 得
得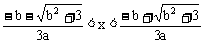
∴
f(x)在(-∞,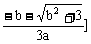 ,
,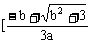 ,+∞)上单调递增;在
,+∞)上单调递增;在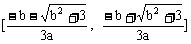 上单调递减。
上单调递减。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com