
3.呈现合作交流
本节课每个问题的波浪式出现,我们不仅发现每个学生动手做、动眼看、动口说、动笔写、动脑想,全身心投入到学习过程中去,真正地让学生动起来,让课堂活起来,更令人吃惊的是“合作交流”发挥得淋漓尽致. 这不仅反映在四人小组毫无掩饰、捏造的交流过程,更有把自己的不同想法敢于同学面前展示和袒露的真实场景. 这种“生生合作”的经典,更来自于“师生合作”的源头. 教师始终把自己放在和学生平等的位置上,“同欢乐,共困苦”,让学生心情愉悦地、神情自信地回答和展示自己的“成果”,这些话成果、说思路、讲道理、议方法、谈感悟等系列活动,既寄托了老师的殷切希望和拳拳爱生之心,又破除了传统的学生蹑手蹑脚演板,胆怯地来回张望,等待老师去评点乃至训斥的那种尴尬局面,展现了一种兴趣盎然、生动活泼的自主、合作、交流的课堂活动场景.
2.彰显理性数学
本节课,无论是对称性,增减性(最大值),及二项式系数和的逐步生成,学生都能从“特殊到一般”的认识规律,归纳猜想到结论. 但数形结合的函数思想,组合数两个性质的运用,两个计数原理的巧妙“会师”,奇数项二项式系数和等于偶数项二项式系数和,反馈升华例示中赋值法再现. 这正是“数学演绎”、“理性数学”的精华,让学生找到内化和建构的多种途径.这不仅会自然增强或辐射到学生的解题能力和理性思维,更能影响和渗透到他们的终身学习和今后从事的工作中去.
1.放手发动学生
把课堂还给学生,一直是课改的大方向,也是新课标的原动力之一. 还给学生什么呢?教师作了很好的诠释:
一是给“问题”,当然问题有预设的,也有生成的,符合从学生“思维最近发展区”出发这一根本教学原则.
二是给“时间”,这体现了教师的先进教学理念,即便是教学难点“中间项系数最大”这一组合数计算讨论过程仍由学生尝试. 当然,n=6,7时,离散型函数的图象起了直观引领,奠基的重要作用. 不为完成任务所累,不为主宰课堂所困.
三是给“机会”,让学生展示自主探索,合作交流的成果,极大地保护和激发了学生学习的热情和积极性,参与程度和激情得到了空前的提高.
本节课,教师在充分挖掘教学内容的内在联系,了解学生已有知识基础,充分分析学情后,确定的教学目标:理解、领悟二项式系数性质;渗透数形结合和分类讨论思想;灵活有效地运用赋值法.应该说具有具体而又准确,科学而有效的特点.随着课堂的实践得到了落实,并且将“知识目标”、“能力目标”、“情感目标”融为一体.
教学目标完全符合学生“认识规律”,以递进的形式呈现:观察分析、归纳猜想、抽象概括,提炼上升;特殊--一般--特殊到一般…,课堂实践表明,这些目标,在师生共同努力及合作下是完全可以达到的.
6. 悬念小结再求索
[课堂小结] 通过本节课的学习,你有什么收获和体会(从数学和生活的角度)?还有什么疑问吗?
[课堂延伸]今天同学们展示了一些杨辉三角的规律,但是作为我国古代数学重要成就之一的杨辉三角还有更多有趣的规律,相信大家一定有极高的热情和严谨的态度去探究与发现杨辉三角的奥妙之处.
[课外活动](研究性学习)
活动主题:杨辉三角中的奥妙.
活动目标:探究与发现杨辉三角中的更多奥妙.
活动方案步骤:查阅资料,收集信息;独立思考,发现规律,猜想证明;合作探究,小组讨论,形成初步结论;与指导老师及其他小组成员交流展示;撰写研究性学习报告.
[设计意图]通过课堂的整理、总结与反思,使学生更好的掌握主干知识,体会探究过程中渗透的数学思想方法,再次感受我国古代数学成就,激励自己努力学习.“杨辉三角”还有很多有趣的规律,让学生带着问题走进课堂,带着疑问离开教室,培养学生自主研修的习惯,提高学生探究问题、解决问题的能力.设计研究性学习活动,诱发学生创造性的想象和推理.同时教会学生如何开展研究性学习.
5. 反馈升华拨思路
练1. 的展开式中的第四项和第八项的二项式系数相等,则
的展开式中的第四项和第八项的二项式系数相等,则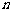 等于
.
等于
.
练2. 的展开式中前 项的二项式系数逐渐增大,后半部分逐渐减小,二项式系数取得最大值的是第 项.
的展开式中前 项的二项式系数逐渐增大,后半部分逐渐减小,二项式系数取得最大值的是第 项.
练3.已知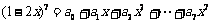 ,求:
,求:
(1) ;(2)
;(2) .
.
[设计意图]促进学生进一步掌握二项式系数的性质,学会用赋值法解决问题,促进其有意识的运用.
4. 合作交流议方法
[继续探究]问题: 展开式的各二项式系数的和是多少?
展开式的各二项式系数的和是多少?
探究:(1)计算 展开式的二项式系数的和(
展开式的二项式系数的和(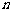 =1,2,3,4,5,6).
=1,2,3,4,5,6).
(2)猜想 展开式的二项式系数的和.
展开式的二项式系数的和.
(3)怎样证明你猜想的结论成立?
赋值法:已知 ,
,
令 ,则
,则 .
.
这就是说, 的展开式的各个二项式系数的和等于
的展开式的各个二项式系数的和等于 .
.
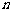 元集合子集的个数(两个计数原理).
元集合子集的个数(两个计数原理).
分类计数原理:
分步计数原理: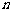 个2相乘,即
个2相乘,即 .
.
所以 .
.
[问题拓展]你能求 吗?
吗?
在展开式 中,令
中,令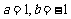 ,
,
则得 ,
,
即 ,所以
,所以 ,
,
在 的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
[设计意图]通过学生归纳猜想各二项式系数的和,引导学生验证猜想结论是否正确;同时为了突破利用赋值法证明二项式系数性质的难点,引导学生从模型化的角度出发,多角度的分析问题、探究问题、解决问题,将学生思维推向高潮,既加深学生对前后知识的内在联系的理解,又从深度和广度上让学生感受数学知识的串联和呼应.
3. 联系旧知探新知
[问题提出]怎样证明 展开式的二项式系数具有对称性和增减性与最大值呢?
展开式的二项式系数具有对称性和增减性与最大值呢?
[问题探究]探究:(1) 展开式的二项式系数
展开式的二项式系数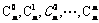 ,
, 可以看成是以
可以看成是以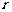 为自变量的函数
为自变量的函数 吗?它的定义域是什么?
吗?它的定义域是什么?
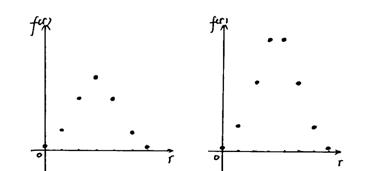 (2)画出
(2)画出 和7时函数
和7时函数 的图象,并观察分析他们是否具有对称性和增减性与最大值.
的图象,并观察分析他们是否具有对称性和增减性与最大值.
(3)结合杨辉三角和所画函数图象说明或证明二项式系数的性质.
对称性:与首末两端“等距离”的两个二项式系数相等. .
.
增减性与最大值: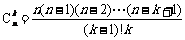
 ,所以
,所以 相对于
相对于 的增减情况由
的增减情况由 决定.由
决定.由 可知,当
可知,当 时,二项式系数是逐渐增大的.由对称性知它的后半部分是逐渐减小的,且在中间取得最大值.当
时,二项式系数是逐渐增大的.由对称性知它的后半部分是逐渐减小的,且在中间取得最大值.当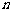 的偶数时,中间的一项取得最大值;当
的偶数时,中间的一项取得最大值;当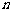 是奇数时,中间的两项
是奇数时,中间的两项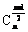 ,
, 相等,且同时取得最大值.
相等,且同时取得最大值.
[设计意图]教师引导学生用函数思想探究二项式系数的性质,学生画图并观察分析图象性质;运用特殊到一般、数形结合的数学思想归纳二项式系数的性质,升华认识;通过分组讨论、自主探究、合作交流,说明或证明二项式系数的对称性和增减性与最大值,提高学生合作意识.
2. 感知规律悟性质
通过课外学习,同学们观察发现了杨辉三角的一些规律,并且知道杨辉三角的第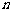 行就是
行就是 展开式的二项式系数,
展开式的二项式系数, 展开式的二项式系数具有杨辉三角同行中的规律--对称性和增减性与最大值.
展开式的二项式系数具有杨辉三角同行中的规律--对称性和增减性与最大值.
[设计意图]寻找二项式系数与杨辉三角的关系,从而让学生理解二项式系数具有杨辉三角同行中的规律.
1. 展示成果话杨辉
课前开展学习活动:了解“杨辉三角”的历史背景、地位和作用,探究与发现“杨辉三角”包含的规律.
(1)学生从不同的角度畅谈“杨辉三角”,对它有何了解及认识.
(2)各小组展示探究与发现的成果--“杨辉三角”包含的一些规律.
[设计意图]引导学生开展课外学习,了解“杨辉三角”,探究与发现“杨辉三角”包含的规律,弘扬我国古代数学文化;展示探究与发现的杨辉三角的规律,为学习二项式系数的性质埋下伏笔.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com