
4、教法特点及预期效果分析
数学是思维的科学,数学学习不是简单的“告诉”,而应是学生个性化的“体验”.
在本节课的学习中,采用问题引导、合作探究的教学方法,设计六大教学环节:展示成果话杨辉、感知规律悟性质、联系旧知探新知、合作交流议方法、反馈升华拨思路、悬念小结再求索.倡导自主探索、独立思考、动手实践、合作交流,为学生开展数学体验,丰富学习方式,形成积极主动的、多样的学习方式创造了有利的条件和广阔的空间.
在探究二项式系数的性质中,设计为探究“三部曲”:
第一步是数形结合、概括性质. 通过学生画出 =6和
=6和 =7时函数图象,并观察分析其对称性和增减性与最大值,引导学生概括性质,学生有目的地动手实践,亲身参与探究活动远比目睹幻灯播放更能体验数学蕴含的规律,使抽象的数学知识直观生成.
=7时函数图象,并观察分析其对称性和增减性与最大值,引导学生概括性质,学生有目的地动手实践,亲身参与探究活动远比目睹幻灯播放更能体验数学蕴含的规律,使抽象的数学知识直观生成.
第二步是分组讨论、证明性质. 在学生初步认识“杨辉三角”包含的规律及“杨辉三角”与二项式系数的关系的基础上,在画出 =6和
=6和 =7时函数图象并观察分析其对称性和增减性与最大值的情境下,采取分组讨论、交流展示的学习方式,诱发学生内在的认知冲突,激发学生沉淀的知识,培养学生解决问题的能力,让知识经历一个再发现、再创造的过程,体验到探究过程中涉及的思维策略,促进学生对内容的深刻理解,把课堂教学的“话语权”、“生成权”、“展示权”、“交流权”交给学生,用学生的“亮点”,点亮学生的智慧.
=7时函数图象并观察分析其对称性和增减性与最大值的情境下,采取分组讨论、交流展示的学习方式,诱发学生内在的认知冲突,激发学生沉淀的知识,培养学生解决问题的能力,让知识经历一个再发现、再创造的过程,体验到探究过程中涉及的思维策略,促进学生对内容的深刻理解,把课堂教学的“话语权”、“生成权”、“展示权”、“交流权”交给学生,用学生的“亮点”,点亮学生的智慧.
第三步是师生合作、再探性质. 在探究各二项式系数的和的教学中,设计探究性的问题串,运用特殊到一般的归纳思想,猜想结论,再运用赋值法证明这一性质,培养学生思维的严谨性和深刻性,引导学生挖掘问题的本质特征,同时呈现用分类和分步计数原理说明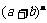 的展开式的各二项式系数的和,引发学生的认知冲突,培养学生思维的灵活性和独创性,激发学生的探索兴趣.
的展开式的各二项式系数的和,引发学生的认知冲突,培养学生思维的灵活性和独创性,激发学生的探索兴趣.
学生经历课前初探、课中深探、变式细探的探究过程,对“杨辉三角”及二项式系数的性质有比较深刻的认识,不断提高学生探究和解决问题的能力,促进学生数学思维发展.
4.通过恰时恰点的问题引入、引申,采用学生课前自主探究、课上合作探究、课下延伸探究的学习方式,培养学生问题意识,提高学生思维能力,孕育学生创新精神,激发学生探索、研究我国古代数学的热情.
3.通过体验“发现规律、寻找联系、探究证明、性质运用”的学习过程,使学生掌握二项式系数的一些性质,体会应用数形结合、特殊到一般进行归纳、赋值法等重要数学思想方法解决问题的“再创造”过程.
2.通过学生从函数的角度研究二项式系数的性质,建立知识的前后联系,体会用函数知识研究问题的方法,培养学生的观察能力和归纳推理能力.
1.通过课前组织学生开展“了解杨辉三角、探究与发现杨辉三角包含的规律”的学习活动,让学生感受我国古代数学成就及其数学美,激发学生的民族自豪感.
2.教学目标分析
“杨辉三角”是我国古代数学重要成就之一,蕴含了丰富的内容,显示了我国古代人民的卓越智慧和才能,了解我国古代数学成就之一的“杨辉三角”包含的规律,结合“杨辉三角”,运用函数的知识深化对二项式系数性质的理解,联系函数图象和性质、赋值法、两个计数原理等知识探究证明二项式系数的性质,体会用函数知识研究问题的方法,体验数形结合、特殊到一般进行归纳等数学思想的渗透和运用,体现教师引导、学生探究的教学方式,培养学生问题意识,提高数学思维能力,培育学生理性精神.
根据以上分析特制定教学目标如下:
1.内容和内容解析
《“杨辉三角”与二项式系数的性质》是全日制普通高级中学教科书人教A版选修2-3第1章第3节第2课时.教科书将二项式系数性质的讨论与“杨辉三角”结合起来,是因为“杨辉三角”蕴含了丰富的内容,由它可以直观看出二项式系数的性质,“杨辉三角”是我国古代数学重要成就之一,显示了我国古代人民的卓越智慧和才能,应抓住这一题材,对学生进行爱国主义教育,激励学生的民族自豪感.本节内容以前面学习的二项式定理为基础,
由于二项式系数组成的数列就是一个离散函数,引导学生从函数的角度研究二项式系数的性质,便于建立知识的前后联系,使学生体会用函数知识研究问题的方法,可以画出它的图象,利用几何直观、数形结合、特殊到一般的数学思想方法进行思考,这对发现规律,形成证明思路等都有好处. 这一过程不仅有利于培养学生的思维能力、理性精神和实践能力;也有利于学生理解数学知识,培养其数学应用意识.
研究二项式系数这组特定的组合数的性质,对巩固二项式定理,建立相关知识之间的联系,进一步认识组合数、进行组合数的计算和变形都有重要的作用,对后续学习微分方程等也具有重要地位.
根据以上对教材及学情的分析,特制定教学重点如下:
体会用函数知识研究问题的方法,理解二项式系数的性质.
教材的主干内容之一“杨辉三角”就蕴含较丰富的文化价值(包括数字演变),我国古代数学成就和爱国主义情结.教学过程中,由于提及到与“帕斯卡三角”的比照,涉及到与“斐波那契数列”的联系,学生的民族自豪感,爱国主义情操不时会写在那一张张稚嫩、率真的脸上,相信对他们的精神风貌是一种陶冶,思想品质是一种升华.
本节课值得改进的地方:
一是可考虑通过网上链接搜集一些“杨辉三角”包含的规律,比较学生展示的结论,让学生享受成功的喜悦,同时激发学生“再求索”的热情;二是学生展示小组讨论增减性与最大值时出现口误,以及教师板书将“各二项式系数的和”写成“各二项式的系数和”,尽管课后通过师生沟通,形成了共识,但值得在以后的教学中更好地把握好教学细节.
综观整节课三个性质的呈现(教师板书的主题)毫无生涩造作,支离隔阂的痕迹. 却是分块搭建,彼此衔接,宛若于活动中生成,从过程中体验,在操作中建构,水到渠成之感,这得益于教师充分挖掘和把握教材内在联系之功力和涵养,也借助于教师过渡衔接之妙:和蔼微笑的教态,激励动情的语言,豁达激情的风貌,使得课堂情境天人合一.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com