3. 设则

向量共线:

向量垂直:，

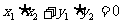
2.平面向量的坐标运算

(1)　　 若，则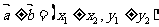

(2)　　 若=(x,y)，则=(x, y)

(3)　　 若，则

1.平面向量的坐标表示：在直角坐标系中，分别取与x轴、y轴方向相同的两个单位向量作为基底。由平面向量的基本定理知，该平面内的任一向量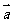可表示成，由于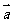与数对(x,y)是一一对应的，因此把(x,y)叫做向量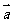的坐标，记作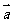=(x,y)，其中x叫作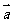在x轴上的坐标，y叫做在y轴上的坐标。

(1) 若,则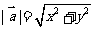

(2)若A(x₁,y₁),B(x₂,y₂)则,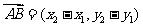

表示相等向量的有向线段的始点、终点的坐标未必相同.

(3) 向量相等ó坐标相同。

2.掌握平面向量的坐标运算,掌握共线向量的坐标表示；

1．理解平面向量的坐标概念;

6.已知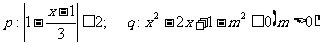，若﹁p 是﹁q的必要不充分条件，求实数m的取值范围.

5.设有两个命题：

(1)关于x的不等式x²+(a－1)x+a²>0的解集是R；

(2)f(x)=是减函数.且(1)和(2)至少有一个为真命题, 求实数a的取值范围.

4. 设命题p:函数f(x)=是R上的减函数，命题q:函数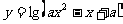的定义域为R，如果“(非p)或q”为假命题，求实数的a取值范围。

3.已知p:,,q:.若非p是q的必要而不充分条件，求实数m的取值范围。

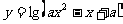2．设命题p:函数f(x)=是R上的减函数，命题q:函数的定义域为R，如果“(非p)或q”为假命题，求实数的a取值范围。