
3. 下列各句中,加点的成语使用恰当的一句是
下列各句中,加点的成语使用恰当的一句是
A.这里有我汗水浸过的土地,这里有我患难与共的亲友,这里有我相濡以沫的妻子,这里有我生命的根。
B.两位阔别多年的老友意外地在一条小巷里狭路相逢,两人又是握手又是拥抱,别提多高兴了。
C.人生就是一条川流不息的奔腾之河,生命则是一曲永无止境的奔腾之歌。
D.这则笑话因为对漠不关心人民疾苦的官员讽刺得很有力量,在民间流传很广,影响极大。
[答案]A
[解析]B狭路相逢:在很窄的路上遇见了,不容易让开。指仇人相遇,难以相容。 C“川流不息”的“川”,河流,与下文“奔腾之河”系同类事物,不能构成比喻。D“漠不关心”不能带宾语“人民疾苦”。
2. 下列各句中,加点的成语使用不恰当的一句是
A.在伊拉克战争期间,一些女记者直接到前线采访,其冒险程度无异于火中取栗。
B.这次巴勒斯坦人士遭暗杀的事件,使得中东和平的前景再一次成为海市蜃楼。
C.美元近期在外汇市场的疲软走势,使长期处于低迷状态的欧洲经济雪上加霜。
D.欧洲一些国家从自身利益考虑,在许多重大国际问题上不再惟美国马首是瞻。
1.下列各项中,加点的成语使用不恰当的一项是
A、土耳其举重选手穆特鲁身高只有1.50米,多次参加世界男子举重56公斤级比赛,拿4金牌如探囊取物,人送绰号“举重神童”。
B.冬天老年人要增加营养,也要适当运动,在户外锻炼时一定要量入为出,以步行为宜,时间最好选在傍晚,还要注意保暖,防止着凉。
C.中国茶艺与日本茶道各有特点,但异曲同工,都强调“和”的精神。中日两国青少年也应以和为贵。为中日睦邻友好多作贡献。
D.北京周边的旅游胜地,笔者去过不少。但六月中下旬的绿树繁花中仍有冰挂高悬在危崖上,这一出人意表的奇景却是第一次见到。
[答案]B
[解析]本题考查正确使用成语。本题做题要特别注意题干,要求选出“使用不恰当的一项”。解答成语题第一、逐字解释成语,运用成语结构特点把握成语大意,但要注意不能望文生义;第二、注意成语潜在的感情色彩和语体色彩;第三、要注意成语使用范围,搭配的对象;第四、弄清所用成语的前后语境,尽可能找出句中相关联的信息;第五、从修饰与被修饰关系上分析,看修饰成分跟中心词之间是否存在前后语义矛盾或者前后语义重复的现象。B量入为出:根据收入的多少来定开支的限度。A探囊取物:伸手到口袋里拿东西。比喻能够轻而易举地办成某件事情。C异曲同工:不同的曲调演得同样好。比喻话的说法不一而用意相同,或一件事情的做法不同而都巧妙地达到目的。D出人意表:出乎人们意料之外。
150. 在矩形ABCD中,AB=a,AD=2b,a<b,E、F分别是
 AD、BC的中点,以EF为折痕把四边形EFCD折起,
AD、BC的中点,以EF为折痕把四边形EFCD折起,
当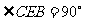 时,二面角C-EF-B的平面角的余
时,二面角C-EF-B的平面角的余
弦值等于 ( )
A.0 B.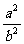 C.
C.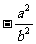 D.
D.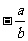
解析:由图可知 CE=BE=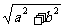 当
当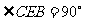 时,CB=
时,CB=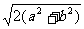 。
。 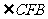 为所求平面角,由余弦定理得cos
为所求平面角,由余弦定理得cos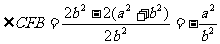 。 选(C)。
。 选(C)。
148. 矩形ABCD,AB=3,BC=4,沿对角线BD把△ABD折起,
使点A在平面BCD上的射影A′落在BC上,求二面角A-BC--C的大小。
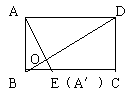
 这是一道由平面图形折叠成立体图形的问题,解决问题的关键在
于搞清折叠前后“变”与“不变”。结果在平面图形中过A作AE⊥BD交BD于O、交BC于E,则折叠后OA、OE与BD的垂直关系不变。但OA与OE此时变成相交两线段并确定一平面,此平面必与棱垂直。由特征Ⅱ可知,面AOE与面ABD、面CBD的交线OA与OE所成的角,即为所求二面角的平面角。另外,A在面BCD上的射影必在OE所在的直线上,又题设射影落在BC上,所以E点就是A′,这样的定位给下面的定量提供了优质服务。事实上,AO=AB·AD/BD=3*4/5=12/5,OA′=OE=BO·tgc∠CBD,而BO=AB2/BD=9/5, tg∠CBD,故OA′=27/20。在Rt△AA′O中,∠AA′O=90°所以cos∠AOA′=A′O/AO=9/16,ty∠AOA′=arccos9/16即所求的二面arccos9/16。
149. 将边长为
这是一道由平面图形折叠成立体图形的问题,解决问题的关键在
于搞清折叠前后“变”与“不变”。结果在平面图形中过A作AE⊥BD交BD于O、交BC于E,则折叠后OA、OE与BD的垂直关系不变。但OA与OE此时变成相交两线段并确定一平面,此平面必与棱垂直。由特征Ⅱ可知,面AOE与面ABD、面CBD的交线OA与OE所成的角,即为所求二面角的平面角。另外,A在面BCD上的射影必在OE所在的直线上,又题设射影落在BC上,所以E点就是A′,这样的定位给下面的定量提供了优质服务。事实上,AO=AB·AD/BD=3*4/5=12/5,OA′=OE=BO·tgc∠CBD,而BO=AB2/BD=9/5, tg∠CBD,故OA′=27/20。在Rt△AA′O中,∠AA′O=90°所以cos∠AOA′=A′O/AO=9/16,ty∠AOA′=arccos9/16即所求的二面arccos9/16。
149. 将边长为 的正方形
的正方形 沿对角线
沿对角线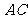 折起,使得
折起,使得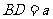 ,则三棱锥
,则三棱锥 -
- 的体积为 ( )
的体积为 ( )
A. 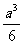 B.
B.
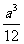 C.
C.
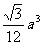 D.
D. 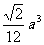
D
解析:取BD的中点为O,BD⊥平面OAC,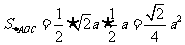 ,则
,则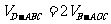 =
=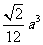 。选D
。选D
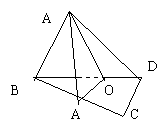
147. 已知Rt△ABC的两直角边AC=2,BC=3,P为斜边上一
点,沿CP将此直角三角形折成直二面角A-CP-B,当AB=71/2时,求二面角P-AC-B的大小。

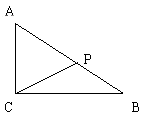 作法一:∵A-CP-B为直角二面角,
∴过B作BD⊥CP交CP的延长线于D,则BD⊥DM APC。
∴过D作DE
⊥AC,垂足为E,连BE。
∴∠DEB为二面角A-CP-B的平面角。
作法二:过P点作PD′⊥PC交BC于D′,则PD′⊥面APC。
∴过D′作D′E′⊥AC,垂足为E′,边PE′,
∴∠D′E′P为二面角P-AC-B的平面角。
作法一:∵A-CP-B为直角二面角,
∴过B作BD⊥CP交CP的延长线于D,则BD⊥DM APC。
∴过D作DE
⊥AC,垂足为E,连BE。
∴∠DEB为二面角A-CP-B的平面角。
作法二:过P点作PD′⊥PC交BC于D′,则PD′⊥面APC。
∴过D′作D′E′⊥AC,垂足为E′,边PE′,
∴∠D′E′P为二面角P-AC-B的平面角。
146. 如图,在梯形ABCD中,AD//BC, ABC=900,AB=a,AD=3a,sin
ABC=900,AB=a,AD=3a,sin ADC=
ADC= ,又PA⊥平面ABCD,PA=a,求二面角P-CD-A的大小。(答案:arctg
,又PA⊥平面ABCD,PA=a,求二面角P-CD-A的大小。(答案:arctg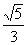 )
)
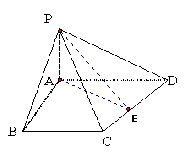

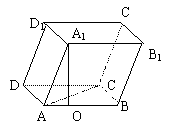
145. 如图,平行六面体ABCD-A1B1C1D1的底面为正方形,点A1在底面的射影O在AB上,已知侧棱A1A与底面ABCD成450角,A1A=a。求二面角A1-AC-B的平面角的正切值。(答案:
如图,平行六面体ABCD-A1B1C1D1的底面为正方形,点A1在底面的射影O在AB上,已知侧棱A1A与底面ABCD成450角,A1A=a。求二面角A1-AC-B的平面角的正切值。(答案: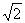 )
)
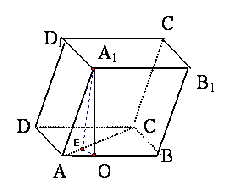
144. 如图,梯形ABCD中,BA⊥AD,CD⊥AD,AB=2,CD=4,P为平面ABCD外一点,平面PAD⊥平面ABCD,△PBC是边长为10的正三角形,求平面PAD与面PBC所成的角.
解法一:如图,延长DA、CB交于E,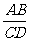 =
=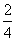 =
=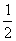 ,∴AB是△ECD的中位线,CB=BE=10.又△PCB为正△,易证△PCE为直角三角形,PE⊥PC.又平面PDA⊥平面ABCD,且CD⊥交线DA,∴CD⊥平面PDE.PE是PC在平面PDE内的射影,∴PE⊥PD(三垂线定理的逆定理).故∠CPD是D-PE-C的平面角.在Rt△CDP中,sin∠DPC=
,∴AB是△ECD的中位线,CB=BE=10.又△PCB为正△,易证△PCE为直角三角形,PE⊥PC.又平面PDA⊥平面ABCD,且CD⊥交线DA,∴CD⊥平面PDE.PE是PC在平面PDE内的射影,∴PE⊥PD(三垂线定理的逆定理).故∠CPD是D-PE-C的平面角.在Rt△CDP中,sin∠DPC=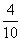 =
=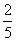 ,故二面角大小为arcsin
,故二面角大小为arcsin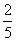 .
.
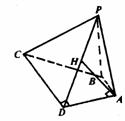 解法二:利用Scosθ=S′.如右图,
解法二:利用Scosθ=S′.如右图,
平面PAD⊥平面ABCD

 CD⊥AD,BA⊥AD
CD⊥AD,BA⊥AD
BA⊥平面PAD

CD⊥平面PAD
△PAD是△PBC在平面PDA内的射影.设面PDA与面PCB所成的二面角为θ,则S△PDA=S△PCB·cosθ.Rt△PAB中,PA=4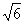 =AD;Rt△PDC中,PD=2
=AD;Rt△PDC中,PD=2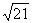 .
.
∴△PAD为等腰三角形且S△PAD=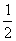 PD·AH=15
PD·AH=15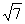 .
.
cosθ=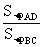 =
=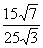 =
=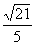 ,
,
 θ=arccos=
θ=arccos=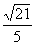 .
.
143. 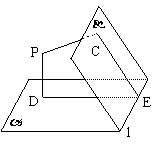 如图,在平面角为600的二面角
如图,在平面角为600的二面角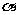 -l-
-l- 内有一点P,P到
内有一点P,P到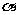 、
、 分别为PC=2cm,PD=3cm,则垂足的连线CD等于多少?(2)P到棱l的距离为多少?
分别为PC=2cm,PD=3cm,则垂足的连线CD等于多少?(2)P到棱l的距离为多少?
解析:对于本题若这么做:过C在平面 内作棱l的垂线,垂足为E,连DE,则
内作棱l的垂线,垂足为E,连DE,则 CED即为二面角的平面角。这么作辅助线看似简单,实际上在证明
CED即为二面角的平面角。这么作辅助线看似简单,实际上在证明 CED为二面角的平面角时会有一个很麻烦的问题,需要证明P、D、E、C四点共面。这儿,可以通过作垂面的方法来作二面角的平面角。
CED为二面角的平面角时会有一个很麻烦的问题,需要证明P、D、E、C四点共面。这儿,可以通过作垂面的方法来作二面角的平面角。
解:∵PC、PD是两条相交直线,
∴PC、PD确定一个平面 ,设
,设 交棱l于E,连CE、DE。
交棱l于E,连CE、DE。
∵PC⊥ , ∴PC⊥l,
, ∴PC⊥l,
又∵PD⊥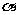 ,∴PD⊥l。
,∴PD⊥l。
∴l⊥平面 ,则l⊥CE、DE,故
,则l⊥CE、DE,故 CED即为二面角的平面角,即
CED即为二面角的平面角,即 CED=600。
CED=600。
∴ CPD=1200,△PCD中,PD=3,PC=2,由余弦定理得CD=
CPD=1200,△PCD中,PD=3,PC=2,由余弦定理得CD= cm。由PD⊥DE,PC⊥CE可得P、D、E、C四点共圆,且PE为直径,由正弦定理得PE=2R=
cm。由PD⊥DE,PC⊥CE可得P、D、E、C四点共圆,且PE为直径,由正弦定理得PE=2R= =
=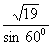 =
=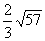 cm。
cm。
说明:三垂线定理及其逆定理是作二面角的平面角的最主要的方法,要引起重视。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com