
2010.四川省自贡市 第二节:句型转换 ,满分2分)
3.设集合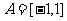 ,
,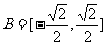 ,函数
,函数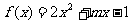
(1)设不等式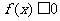 的解集为C,当
的解集为C,当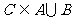 时,求实数
时,求实数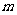 的取值范围;
的取值范围;
(2)若对任意实数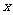 ,均有
,均有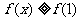 恒成立,求
恒成立,求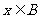 时,
时,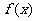 的值域;
的值域;
(3)当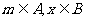 时,证明
时,证明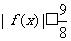
答案:(1)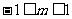 (2)
(2)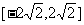
(3)因为对称轴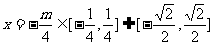 ,
,
故只需证明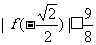 ,
,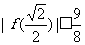 ,
,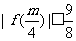 即可
即可
2.已知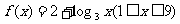 ,求函数
,求函数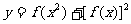 的最大值和最小值,并求取最大值和最小值的相应的
的最大值和最小值,并求取最大值和最小值的相应的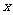 的值
的值
答案: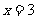 时,
时,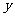 取最大值13;
取最大值13;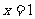 时,
时,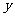 取最小值6
取最小值6
1.某农工贸集团开发的养殖业和养殖加工生产业的年利润分别是T和Q(万元),这两项生产与投入的奖金a(万元)的关系是P=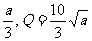 ,该集团今年计划对这两项生产共投入奖金60万元,为获得最大利润,对养殖业与养殖加工生产业投入应各为多少万元?最大利润为多少万元?
,该集团今年计划对这两项生产共投入奖金60万元,为获得最大利润,对养殖业与养殖加工生产业投入应各为多少万元?最大利润为多少万元?
解:设投入养殖业为x万元,则投入养殖加工生产业为60-x万元
由题意:P+Q=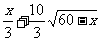 (0≤x≤60)
(0≤x≤60)
设t=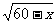 ,则0≤t≤
,则0≤t≤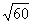 ,x=60-t
,x=60-t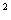
P+Q=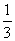 (60-t
(60-t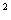 )+
)+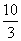 t=-
t=-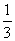 (t-5)
(t-5)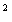 +
+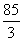
∴当t=5时,即x=35时,(P+Q)max=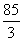 .
.
∴对养殖业投入35万元,对养殖加工生产业投入25万元,可获最大利润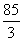 万元.
万元.
本节学习了二次函数在给定区间上求最值的方法,把握数形结合的特征与方法,逐步掌握函数思想在实际问题中的应用.
已知f(x)=x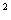 -4x-4,x∈[t,t+1](t∈R),求f(x)的最小值φ(t)的解析式.
-4x-4,x∈[t,t+1](t∈R),求f(x)的最小值φ(t)的解析式.
解:f(x)=(x-2)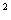 -8
-8
(1)当2∈[t,t+1]时,即1<t<2时,φ(t)=f(2)=-8.
(2)当t>2时,f(x)在[t,t+1]上是增函数,故φ(t)=f(t)=t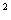 -4t-4.
-4t-4.
(3)当t+1<2,即t<1时,f(x)在[t,t+1]上是减函数.
故φ(t)=f(t+1)=t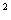 -2t-7
-2t-7
综上所述:φ(t)=
例1若函数f(x)=x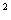 +bx+c对任意实数x都有f(2+x)=f(2-x),那么( )
+bx+c对任意实数x都有f(2+x)=f(2-x),那么( )
A.f(2)<f(1)<f(4) B.f(1)<f(2)<f(4)
C.f(2)<f(4)<f(1) D.f(4)<f(2)<f(1)
分析:此题解决的关键是将函数的对称语言转化为对称轴方程.
解:由f(2+x)=f(2-x)可知:函数f(x)的对称轴为x=2,由二次函数f(x)开口方向向,可得f(2)最小,又f(4)=f(2+2)=f(2-2)=f(0)
在x<2时,y=f(x)为减函数
∵0<1<2,∴f(0)>f(1)>f(2)
即f(2)<f(1)<f(4)答案:A
通过此题可将对称语言推广如下:
(1)若对任意实数x,都有f(a+x)=f(a-x)成立,则x=a是函数f(x)的对称轴
(2)若对任意实数x,都有f(a+x)=f(b-x)成立,则x=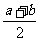 是f(x)的对称轴.
是f(x)的对称轴.
例2求f(x)=x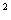 -2ax+2在[2,4]上的最大值和最小值.
-2ax+2在[2,4]上的最大值和最小值.
解:先求最小值.
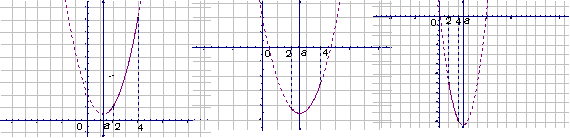
因为f(x)的对称轴是x=a,可分以下三种情况:
(1)当a<2时,f(x)在[2,4]上为增函数,所以f(x)min=f(2)=6-4a;
(2)当2≤a<4时,f(a)为最小值,f(x)min=2-a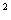 ;
;
(3)当a>4时,f(x)在[2,4]上为减函数,所以f(x)min=f(4)=18-8a
综上所述:f(x)min=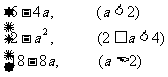
最大值为f(2)与f(4)中较大者:f(2)-f(4)=(6-4a)-(18-8a)=12+4a
(1)当a≥3时,f(2)≥f(4),则f(x)max=f(2)=6-4a;
 (2)当a<3时,f(2)<f(4),则f(x)max=f(4)=18-8a.
(2)当a<3时,f(2)<f(4),则f(x)max=f(4)=18-8a.
故f(x)max=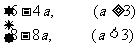
评述:本题属于二次函数在给定区间上的最值问题,由于二次函数的系数含有参数,对称轴是变动的,属于“轴动区间定”,由于图象开口向上,所以求最小值要根据对称轴x=a与区间[2,4]的位置关系,分三种情况讨论;最大值在端点取得时,只须比较f(2)与f(4)的大小,按两种情况讨论即可,实质上是讨论对称轴位于区间中点的左、右两种情况.
例3已知f(x)=|lgx|,且0<a<b<c,若?f(b)<f(a)<f(c),则下列一定成立的是( )
A.a<1,b<1,且c>1 B.0<a<1,b>1且c>1
C.b>1,c>1
D. c>1且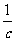 <a<1,a<b<
<a<1,a<b<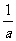
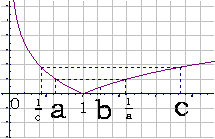 分析:画出y=|lgx|的图象如图:f(x)在(0,1)内是减函数,在(1,+∞)上为增函数.
分析:画出y=|lgx|的图象如图:f(x)在(0,1)内是减函数,在(1,+∞)上为增函数.
观察图象,因为f(a)<f(b)<f(c),所以c>1且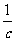 <a<1,a<b<
<a<1,a<b<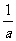 .答案:D
.答案:D
评述:通过此题体会数形结合思想,体会函数图象在函数单调性问题中的应用.
例4函数f(x)=x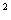 -bx+c,满足对于任何x∈R都有f(1+x)=f(1-x),且f(0)=3,则f(b
-bx+c,满足对于任何x∈R都有f(1+x)=f(1-x),且f(0)=3,则f(b )与f(c
)与f(c )的大小关系是( )
)的大小关系是( )
A.f(b )≤f(c
)≤f(c )
B.f(b
)
B.f(b )≥f(c
)≥f(c )
)
C.f(b )<f(c
)<f(c )
D.f(b
)
D.f(b )>f(c
)>f(c )
)
分析:由对称语言f(1+x)=f(1-x)可以确定函数对称轴,从而确定b值,再由f(0)=3,可确定c值,然后结合b ,c
,c 的大小关系及二次函数的单调区间使问题得以解决.
的大小关系及二次函数的单调区间使问题得以解决.
解:∵f(1+x)=f(1-x)∴f(x)的对称轴x=-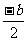 =1
=1
∴b=2,又f(0)=3,∴c=3,
∴f(x)=x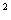 -2x+3
-2x+3
(1)当x>0时,1<2 <3
<3 ,且f(x)在[1,+∞
,且f(x)在[1,+∞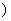 上是增函数
上是增函数
所以f(2 )<f(3
)<f(3 ),即f(b
),即f(b )<f(c
)<f(c )
)
(2)当x<0时,1>2 >3
>3 ,且f(x)在(-∞,1)上是减函数,所以f(2
,且f(x)在(-∞,1)上是减函数,所以f(2 )<f(3
)<f(3 ),即f(b
),即f(b )<f(c
)<f(c )
)
(3)当x=0时,2 =3
=3 =1
=1
则f(2 )=f(3
)=f(3 ),即f(b
),即f(b )=f(c
)=f(c )
)
综上所述,f(b )≤f(c
)≤f(c ).
).
答案:A
通过上一节学习,大家了解了本章内容的整体结构,明确了本章的重难点知识,并熟悉了有关函数的基本概念和基本方法,这一节,我们将通过例题分析重点掌握数形结合的特征与方法,并进一步认清函数的思想实质,进而掌握其应用.
19. What is mainly discussed in the text?
A. Clothesline drying: a way to save energy and money.
B. Clothesline drying: a lost art rediscovered.
C. Opposite opinions on clothesline drying.
D. Different varieties of clotheslines.
答案点击
(一)1.D 2.A3.A 4.C5.C6.B7.D8.C9.A10.D11.D12.B13.D14.A15.B16.C17 C 18A 19A 20.B
(二)1 .A2.D3.C4.B5B 6.B 7C 8D9C 10A 11.B 12.A13C14.C 15. A16.B17. D18. B19. C
18. Who are in favor of clothesline drying?
A. housing businesses. B. Environmentalists.
C. Homeowners Associations. D. Reck’s dissatisfied neighbors.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com