
5.发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后
经点火,使其沿椭圆轨道2运行,最后再次点火,将卫星送
入同步圆轨道3.轨道1、2相切于Q点,轨道2、3相切于P
点(如图1所示).则当卫星分别在1、2、3轨道上正常运行
时,以下说法正确的是 ( ) 图1
A.卫星在轨道3上的速率大于在轨道1上的速率
B.卫星在轨道3上的角速度大于在轨道1上的角速度
C.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度
D.卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度
解析:卫星在半径为r的轨道上运行时,速度v= ,可见轨道半径r越大,
运行速度越小,由v=ωr可得ω= ,r越大,ω越小,A、B均错;卫星的向
心加速度由万有引力产生,在不同的轨道上运动时,由a=知,在同一点它们的
加速度是相同的,故C错D正确.
答案:D
4.(2010·汕头模拟)有一宇宙飞船到了某行星上(该行星没有自转运动),以速度v接近
行星表面匀速飞行,测出运动的周期为T,已知引力常量为G,则以下说法不正确的
是 ( )
A.该行星的半径为
B.该行星的平均密度为
C.无法测出该行星的质量
D.该行星表面的重力加速度为
解析:由T=可得:R=,A正确;由=m可得:M=,C错误;
由M=πR3·ρ得:ρ=,B正确;由=mg得:g=,D正确.
 答案:C
答案:C
3.宇宙中两个星球可以组成双星,它们只在相互间的万有引力作用下,绕球心连线的
某点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢
增加,设双星仍做匀速圆周运动,则下列说法错误的是 ( )
A.双星相互间的万有引力减小
B.双星做圆周运动的角速度增大
C.双星做圆周运动的周期增大
D.双星做圆周运动的半径增大
解析:距离增大万有引力减小,A正确;由m1r1ω2=m2r2ω2及r1+r2=r得,r1=,
r2=,可知D正确;F=G=m1r1ω2=m2r2ω2,r增大F减小,r1增大,
故ω减小,B错;由T=知C正确.
答案:B
2.(2009·安徽高考)2009年2月11日,俄罗斯的“宇宙-2251”卫星和美国的“铱-
33”卫星在西伯利亚上空约805 km处发生碰撞.这是历史上首次发生的完整在轨卫
星碰撞事件.碰撞过程中产生的大量碎片可能会影响太空环境.假定有甲、乙两块
碎片,绕地球运动的轨道都是圆,甲的运行速率比乙的大,则下列说法中正确的是
( )
A.甲的运行周期一定比乙的长
B.甲距地面的高度一定比乙的高
C.甲的向心力一定比乙的小
D.甲的加速度一定比乙的大
解析:万有引力提供碎片做圆周运动的向心力,=m,解得v= ,因
为甲的速率较大,所以甲的轨道半径较小,B错误.根据周期公式T==2π
可知,甲的运行周期较小,所以A错误.根据加速度公式a=可知甲的加速度较
大,所以D正确.因甲、乙碎片质量未知,不能确定甲、乙向心力的大小关系,所
以C错误.
答案:D
1.(2010·佛山模拟)2009年8月25日韩国用运载火箭“罗老号”将一颗近地科学技术
卫星送入太空,卫星未能进入预定轨道已坠毁;我国于2009年8月31日发射的“帕
拉帕-D”同步卫星,于2009年9月1日在近地点进行了成功变轨,则关于两卫星
的说法不正确的是 ( )
A.“帕拉帕-D”近地点变轨前后,其轨道半长轴的三次方与周期的二次方比值
不变
B.两卫星的设计轨道半长轴的三次方与设计周期二次方比值相同
C.韩卫星坠毁过程中,卫星所受万有引力大于其做圆周运动所需向心力
D.“帕拉帕-D”近地点变轨前后,万有引力对卫星做负功,卫星机械能不变
解析:由开普勒行星运动定律易知A、B正确;韩卫星在坠毁过程中,卫星做向心运
动,则卫星所受万有引力大于其做圆周运动所需向心力,C正确;“帕拉帕-D”近
地点变轨过程中,万有引力对卫星做负功,机械能增加,D项错误;综上所述只有D
项符合题意.
答案:D
(三)解答题
13、要使不等式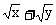 ≤
≤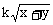 对所有正数x,y都成立,试问k的最小值是多少?
对所有正数x,y都成立,试问k的最小值是多少?
14、解关于x的不等式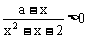
15、已知a≠0,求证: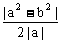 ≥
≥
16、已知不等式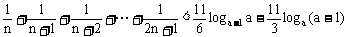 对n∈N+都成立,试求实数a的取值范围。
对n∈N+都成立,试求实数a的取值范围。
17、若a是正实数,2a2+3b2=10,求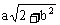 的最值。
的最值。
18、商店经销某商品,年销售量为D件,每件商品库存费用为I元,每批进货量为Q件,每次进货所需费用为S元,现假定商店在卖完该货物时立即进货,使库存量平均为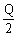 件,问每批进货量Q为多大时,整个费用最省?
件,问每批进货量Q为多大时,整个费用最省?
(二)填空题
9、设a>0,b>0,a,b是常数,则当x>0时,函数f(x)=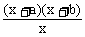 的最小值是______。
的最小值是______。
10、周长为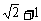 的直角三角形面积的最大值为__________。
的直角三角形面积的最大值为__________。
11、记S=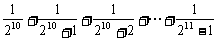 ,则S与1的大小关系是__________。
,则S与1的大小关系是__________。
12、不等式|x2-2x+3|<|3x-1|的解集为__________。
(一)选择题
1、“a>0且b>0”是“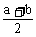 ≥
≥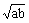 ”的
”的
A、充分而非必要条件 B、必要而非充要条件 C、充要条件 D、既非充分又非必要条件
2、设a<0,则关于x的不等式42x2+ax-a2<0的解集为
A、( ) B、(
) B、(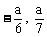 ) C、(
) C、( ) D、φ
) D、φ
3、若0<a<b且a+b=1,则四个数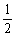 ,b,2ab,a2+b2中最大的是
,b,2ab,a2+b2中最大的是
A、 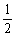 B、b
C、2ab
D、a2+b2
B、b
C、2ab
D、a2+b2
4、已知x>0,f(x)=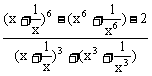 ,则
,则
A、f(x)≤2 B、f(x)≥10 C、f(x)≥6 D、f(x)≤3
5、已知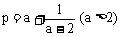 ,
,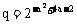 (a>2),则
(a>2),则
A、 p>q B、p<q C、p≥q D、p≤q
6、若|a-c|<h, |b-c|<h,则下列不等式一定成立的是
A、 |a-b|<2h B、|a-b|>2h C、|a-b|<h D、|a-b|>h
7、关于x的方程9x+(a+4)·3x+4=0有解,则实数a的取值范围是
A、 (-∞,-8]∪[0,+∞) B、(-∞,-4)
B、 [-8,4) D、(-∞,-8]
8、若a>0,b>0,且2a+b=1,则S=2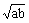 -4a2-b2的最大值是
-4a2-b2的最大值是
A、 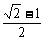 B、
B、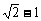 C、
C、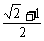 D、
D、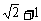
2、本题还可用线性规划知识求解。
例2、 设a>0,b>0,求证: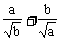 ≥
≥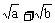 。
。
解题思路分析:
法一:比差法,当不等式是代数不等式时,常用比差法,比差法的三步骤即为函数单调性证明的步骤。
左-右=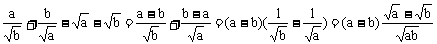
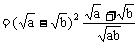 ≥0
≥0
∴ 左≥右
法二:基本不等式
根据不等号的方向应自左向右进行缩小,为了出现右边的整式形式,用配方的技巧。
∵
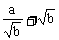 ≥
≥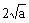
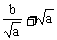 ≥
≥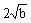
∴
两式相加得: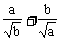 ≥
≥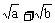
例3、 设实数x,y满足y+x2=0,0<a<1,求证: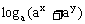 ≤
≤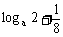 。
。
解题思路分析:
∵
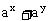 ≥
≥ ,
,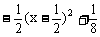 ≤
≤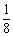 ,0<a<1
,0<a<1
∴
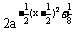 ≥
≥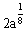
∴
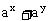 ≥
≥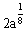
∴
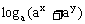 ≤
≤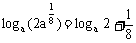
说明:本题在放缩过程中,利用了函数的单调性,函数知识与不等式是紧密相连的。
例4、已知a,b为正常数,x,y为正实数,且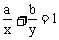 ,求x+y的最小值。
,求x+y的最小值。
解题思路分析:
法一:直接利用基本不等式: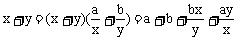 ≥
≥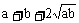 当且仅当
当且仅当 ,即
,即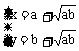 时等号成立
时等号成立
说明:为了使得等号成立,本题利用了“1”的逆代换。
法二:消元为一元函数
途径一:由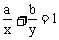 得
得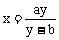
∴
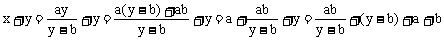
∵ x>0,y>0,a>0
∴
由 >0得y-b>0
>0得y-b>0
∴
x+y≥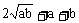
当且仅当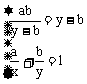 ,即
,即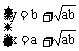 时,等号成立
时,等号成立
途径二:令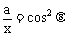 ,
,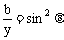 ,
, ∈(0,
∈(0,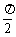 )
)
∴
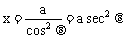 ,
,
∴
x+y=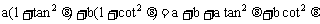 ≥
≥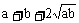
当且仅当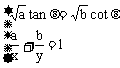 时,等号成立
时,等号成立
说明:本题从代数消元或三角换元两种途径起到了消元作用。
例5、已知f(x)=-3x2+a(6-a)x+b
(1)解关于a的不等式f(1)>0;
(2)当不等式f(x)>0的解集为(-1,3)时,求实数a,b的值。
解题思路分析:
(1)f(1)=-3+a(6-a)+b=-a2+6a+b-3
∵ f(1)>0
∴ a2-6a+3-b<0
△=24+4b
当b≤-6时,△≤0
∴ f(1)>0的解集为φ;
当b>-6时,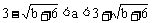
∴
f(1)>0的解集为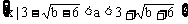
(2)∵ 不等式-3x2+a(6-a)x+b>0的解集为(-1,3)
∴ f(x)>0与不等式(x+1)(x-3)<0同解
∵ 3x2-a(6-a)x-b<0解集为(-1,3)
∴
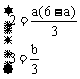
解之得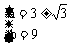
例6、设a,b∈R,关于x方程x2+ax+b=0的实根为α,β,若|a|+|b|<1,求证:
|α|<1,|β|<1。
解题思路分析:
在不等式、方程、函数的综合题中,通常以函数为中心。
法一:令f(x)=x2+ax+b
则 f(1)=1+a+b>1-(|a|+|b|)>1-1=0
f(-1)=1-a+b>1-(|a|+|b|)>0
又∵ 0<|a|≤|a|+|b|<1
∴ -1<a<1
∴
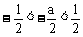
∴ f(x)=0的两根在(-1,1)内,即|α|<1,|β|<1
法二:∵α+β=-a,αβ=b
∴ |α+β|+|αβ|=|α|+|β|<1
∴ |α|-|β|+|α||β|<|α+β|+|αβ|<1
∴(|α|-1)(|β|+1)<0
∵ |β|+1>0
∴ |α|<1
同理:|β|<1
说明:对绝对值不等式的处理技巧是适度放缩,如|a|-|b|≤|a+b|及|b|-|a|≤|a±b|的选择等。
例7、某人乘坐出租车从A地到乙地,有两种方案:第一种方案,乘起步价为10元,每km价1.2元的出租车;第二种方案,乘起步价为8元,每km价1.4元的出租车,按出租车管理条例,在起步价内,不同型号的出租车行驶的里路是相等的,则此人从A地到B地选择哪一种方案比较适合?
解题思路分析:
设A地到B地距离为mkm,起步价内行驶的路为akm
显然,当m≤a时,选起步价为8元的出租车比较合适
当m>a时,设m=a+x(x>0),乘坐起步价为10元的出租车费用为P(x)元,乘坐起步价为8元的出租车费用为Q(x)元,则P(x)=10+1.2x,Q(x)=8+1.4x
∵ P(x)-Q(x)=2-0.2x=0.2(10-x)
∴ 当x>0时,P(x)<Q(x),此时起步价为10元的出租车比较合适
当x<10时,P(x)>Q(x),此时选起步价为8元的出租车比较合适
当x=10时,此时两种出租车任选
2、本题典型错误是从-4≤a-c≤-1,-1≤4a-c≤5中解出a,c的范围,然后再用不等式的运算性质求f(3)=9a-c的范围。错误的原因是多次运用不等式的运算性质时,不等式之间出现了不等价变形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com