
启发式探索法
等可能性事件的判断以及如何求某个事件所包含的基本事件数。
等可能性事件的概率的意义及其求法。
(1)知识与技能目标:了解等可能性事件的概率的意义,运用枚举法计算一些等可能性事件的概率。
(2)过程和方法目标:通过生活中实际问题的引入来创设情境,将一些生活问题构建成一个等可能性事件模型,学生的构建思维能力得到提升;在归纳定义时用到特殊到一般的思想;在解题时利用类比的方法,举一反三。通过枚举法、图表法、排列的基础知识来计算一些等可能性事件的概率,学生对古典概型有个更深刻的理解。
(3)情感与态度目标:感受到亲切、和谐的学习氛围,在活动中进一步发展学生合作交流的意识和能力。了解部分数学史,知道随机事件的发生既有随机性,又有规律性,了解偶然性寓于必然性之中的辩证思想,培养学生的综合素质。
2.预期效果分析
通过本节课的教学,学生应能掌握独立性检验的操作步骤,并能够解决相关的实际问题,同时也可以初步体会到独立性检验的大致思想.而对独立性检验思想的更进一步认识和一些细节性的说法,则应该放在下一个课时,通过更多正面和反面的例子予以进行.
1. 教学特点
① 用学案辅助教学
由于本节内容较散,理论部分较难,故需教师精心设计学案,提前发放给学生,以提高学生的预习效率.
② “问题串”为主,“讲授式”为辅的教学模式
在最初定夺本节课教学模式时比较为难,一方面,按照新课标的理念,注重学生自主探究为主,教师仅仅是引导者(实践证明这有利于学生学会“学习”,尤其是提高自学能力和合作学习能力),然而另一方面,本节内容理论难度较大,而且涉及到很多大学数学的内容,凭高中学生的数学水平难以完成自主探究.因此,在理论部分,还得需要教师讲,教师的“讲授”成为了无奈的选择.不过好在《课程标准》中,不要求学生掌握这部分深奥的理论,只要体会独立性检验的思想,掌握独立性检验的操作步骤.因此,最终定下来的教学模式是“‘问题串’为主,‘讲授式’为辅”的模式.
在“问题串”的指引下,学生研究出解决问题所需要收集的数据,并自行研究课本上给出的解题过程,提炼出解决问题的操作步骤,然后再由教师讲解操作规程背后的理论依据.
③ 游戏式导入
本节课采用“有奖竞猜”的游戏方式作为课堂导入,提高了学生的学习热情.奖品为本节课的录像光盘,也有一定的纪念意义.
④ 充满生活气息的数学课堂
在《课程标准》理念下,“数学在生活中的应用”地位空前提高,教材中引入、例题甚至是课后习题的编写,都有大量生活的影子.而本节课《独立性检验》正是一个贴近生活的数学范畴,它可以解决两件扑朔迷离事情之间到底有关还是无关的问题.因此本课从引入(吸烟与患肺癌)到例题(秃顶与心脏病)到练习(经常上网与考试及格)再到课后作业题,全部都有着实际生活的影子.
4.为什么在最后表达结论的时候要出现“在犯错误的概率不超过XX的前提下”这样的词.
这也是初学者较难理解的问题,原因就在于独立性检验的过程中存在一个小小的漏洞,就是假设“在一次实验中,小概率事件不发生”,而事实上,小概率事件是可能发生的(用反证法,如果始终不发生,就是不可能事件了),而正是因为这一点点漏洞,导致独立性检验的结果可能是错误的,但是犯错误的概率不会太大,我们就把犯错误的最大概率等同于小概率事件发生的概率了。至于小概率事件所对应的临界值,则属于大学的研究范畴,在此不必做过多解释.
3.独立性检验的一般步骤是什么?
由于教材一边解决问题,一边做讲解,因此结题思路显得有点散。然而细心提炼则不难总结出步骤,具体可大致分为4个阶段:①提出原假设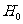 :两个分类变量独立(无关),备择假设
:两个分类变量独立(无关),备择假设 :两个分类变量有关,并假设
:两个分类变量有关,并假设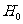 成立;②确定允许犯错误的概率的上界
成立;②确定允许犯错误的概率的上界 ,找到临界值
,找到临界值 ;③在
;③在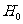 下,计算
下,计算 的观测值
的观测值 ;④若
;④若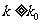 ,此时小概率事件发生,我们认为在一次试验中,小概率事件是不可能发生,所以假设
,此时小概率事件发生,我们认为在一次试验中,小概率事件是不可能发生,所以假设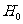 出错,从而接受
出错,从而接受 ;若
;若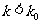 时,我们没有充分理由拒绝
时,我们没有充分理由拒绝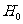 ,也就没办法接受
,也就没办法接受 了.其中②③两个步骤属平级关系,可以调换次序.
了.其中②③两个步骤属平级关系,可以调换次序.
2.如何理解独立性检验的基本思想?
这个问题需要和反证法做一个对比,学生可以通过完成表格(印在学案上)以对二者的基本思想作比较并加以区别。表格内容如下:
|
|
反证法思想 |
用于独立性检验的假设检验思想 |
|
目标 |
证明结论成立 结果只有一种情况:结论成立 |
判断分类变量X与Y之间是否有关 结果有两种可能:有关或无关 |
|
构造 两种 情况 |
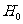 :结论成立 :结论成立  :结论的反面成立 :结论的反面成立 |
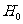 :X与Y之间无关(独立) :X与Y之间无关(独立) :X与Y之间有关 :X与Y之间有关 |
|
理论 依据 |
矛盾双方不可能同时成立 但是有且只有一个成立 |
在一次试验中,小概率事件(观测值 大于等于临界值 大于等于临界值 )几乎是不可能发生的 )几乎是不可能发生的 |
|
操作 步骤 |
1) 假设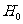 的反面 的反面 成立 成立2) 推导矛盾,从而  不成立 不成立3) 由  不成立说明 不成立说明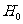 成立 成立 |
1)确定置信水平,找到临界值 2)提出原假设 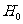 ,并假设 ,并假设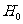 成立, 成立, 3)计算统计量  的观测值 的观测值 4)通过比较  与 与 的大小给出结论: 的大小给出结论: 小则有利于 小则有利于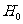 成立, 成立, 大有利于 大有利于 成立 成立 |
基于对学生已有数学水平的分析,在本节新学内容时,有以下几点是初学者不易理解或掌握的:
1. 的结构比较奇怪,来的也比较突然,学生可能会提出疑问.
的结构比较奇怪,来的也比较突然,学生可能会提出疑问.
关于这个问题的处理,要首先利用好前面对“比例”或者两个分类变量“独立”的分析。借助两件事独立的定义以及样本容量较大时可以用频率近似表示概率,可以得到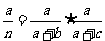 ,考虑到近似造成的误差,
,考虑到近似造成的误差,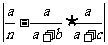 未必恰好为0,但不会太大,于是这个值的平方占概率乘积的比例
未必恰好为0,但不会太大,于是这个值的平方占概率乘积的比例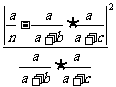 应该较小。由于
应该较小。由于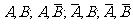 四对事件的独立具有等价性,故加和之后
四对事件的独立具有等价性,故加和之后 应该很小,而将此式化简之后 即得
应该很小,而将此式化简之后 即得 的表达式
的表达式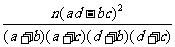 (这个推导过程是我借鉴人教B版教材相应章节知识内容获悉的).另,由此可知
(这个推导过程是我借鉴人教B版教材相应章节知识内容获悉的).另,由此可知 越小说明两件事越“独立”,因此当它小于临界值时有利于说明二者独立,大于或等于临界值时,有利于说明二者相关.
越小说明两件事越“独立”,因此当它小于临界值时有利于说明二者独立,大于或等于临界值时,有利于说明二者相关.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com