
2.“设而不求”是解题(2)的一个亮点.在解直线与圆锥曲线交点、弦长、斜率等问题时,利用韦达定理、中点公式作整体代换处理,是简洁高效化难为易的好方法。
[例1]画出方程log(1+y)x+log(1─y)x=2 log(1+y)x ×
log(1─y)x的曲线
解:x>0, 1+y>0, 1─y>0, 1+y¹1, 1─y¹1Þ─1<y<1,y¹0, x>0
(1)当x=1时,─1<y<1, y¹0;
(2)当x>0,x¹1时
∴ 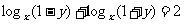 Þlogx(1─y2)=2Þx2+y2=1
(x>0, x¹1)
Þlogx(1─y2)=2Þx2+y2=1
(x>0, x¹1)
结合(1) (2)画出图形
◆特别提示:要注意对曲线方程中变量的范围进行讨论.
[例2]已知⊙O方程为x2+y2=4,定点A(4,0),求过点A且和⊙O相切的动圆圆心的轨迹.
分析:两圆外切,连心线长等于两圆半径之和,两圆内切,连心线长等于两圆半径之差,由此可得到动圆圆心在运动中所应满足的几何条件,然后将这个几何条件坐标化,即得到它的轨迹方程.
解法一:设动圆圆心为P(x,y),因为动圆过定点A,所以|PA|即动圆半径.
当动圆P与⊙O外切时,|PO|=|PA|+2;
当动圆P与⊙O内切时,|PO|=|PA|-2.
综合这两种情况,得||PO|-|PA||=2.
将此关系式坐标化,得
|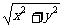 -
-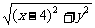 |=2.
|=2.
化简可得(x-2)2-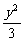 =1.
=1.
解法二:由解法一可得动点P满足几何关系
||OP|-|PA||=2,
即P点到两定点O、A的距离差的绝对值为定值2,所以P点轨迹是以O、A为焦点,2为实轴长的双曲线,中心在OA中点(2,0),实半轴长a=1,半焦距c=2,虚半轴长b=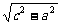 =
=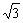 ,所以轨迹方程为(x-2)2-
,所以轨迹方程为(x-2)2-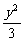 =1.
=1.
提炼方法: 法1是直接法,把动点满足的几何条件转化为坐标表示;
法2是定义法,先定曲线类型(由曲线定义),再求有关参数.是一种常用方法.
③解直线和二次曲线交点问题时,要注意相交必有“Δ>0”的条件。
[例3](2006陕西)如图,三定点A(2,1),B(0,-1),C(-2,1); 三动点D,E,M满足=t, = t , =t , t∈[0,1] (Ⅰ) 求动直线DE斜率的变化范围; (Ⅱ)求动点M的轨迹方程
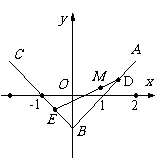 解法一: 如图, (Ⅰ)设D(xD,yD),E(xE,yE),M(x,y)
解法一: 如图, (Ⅰ)设D(xD,yD),E(xE,yE),M(x,y)
由=t, = t ,
知(xD-2,yD-1)=t(-2,-2)
∴ 同理
∴kDE = = = 1-2t
∴t∈[0,1] , ∴kDE∈[-1,1]
(Ⅱ) ∵=t
∴(x+2t-2,y+2t-1)=t(-2t+2t-2,2t-1+2t-1)
=t(-2,4t-2)=(-2t,4t2-2t)
∴ , ∴y= , 即x2=4y
∵t∈[0,1], x=2(1-2t)∈[-2,2]
即所求轨迹方程为: x2=4y, x∈[-2,2]
解法二: (Ⅰ)同上
(Ⅱ) 如图, =+ = + t = + t(-) = (1-t) +t,
= + = +t = +t(-) =(1-t) +t,
= += + t= +t(-)=(1-t) + t
= (1-t2) + 2(1-t)t+t2
设M点的坐标为(x,y),由=(2,1), =(0,-1), =(-2,1)得
消去t得x2=4y,
∵t∈[0,1], x∈[-2,2]
故所求轨迹方程为: x2=4y, x∈[-2,2]
◆提炼方法:①参数法求主程的关键是合理选择参数,本题以决定动点的实数t为参数是显而易见的;
②参数法求方程的主要任务是消参,本题用代入消元法消去了两个参数x0,y0,在设点参数时,经常使用这种消元技巧
 [例4](2005北京) 如图,直线l1:
[例4](2005北京) 如图,直线l1: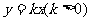 与直线l2:
与直线l2: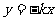 之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
之间的阴影区域(不含边界)记为W,其左半部分记为W1,右半部分记为W2.
(Ⅰ)分别用不等式组表示W1和W2;
(Ⅱ)若区域W中的动点P(x,y)到l1,l2的距离之积等于d2,求点P的轨迹C的方程;
(Ⅲ)设不过原点O的直线l与(Ⅱ)中的曲线C相交于M1,M2两点,且与l1,l2分别
交于M3,M4两点. 求证△OM1M2的重心与△OM3M4的重心重合.
解:(I)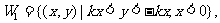
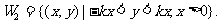
(II)直线 由题意得
由题意得

(III)当直线l与x轴垂直时,可设直线l的方程为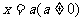 . 由于直线l,曲线C关于x轴对称,且l1与l2关于x轴对称,于是M1M2,M3M4的中点坐标都为(a,0),所以△OM1M2,△OM3M4的重心坐标都为
. 由于直线l,曲线C关于x轴对称,且l1与l2关于x轴对称,于是M1M2,M3M4的中点坐标都为(a,0),所以△OM1M2,△OM3M4的重心坐标都为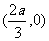 ,即它们的重心重合.
,即它们的重心重合.
当直线l与x轴不垂直时,设直线l的方程为
由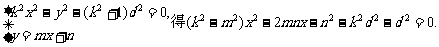
由直线l与曲线C有两个不同交点,可知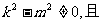

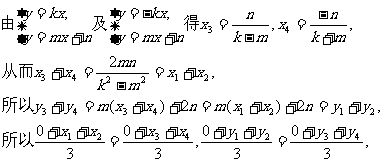
于是△OM1M2的重心与△OM3M4的重心也重合.
[研讨.欣赏]已知常数a>0,向量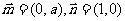 ,经过定点A(0,-a)以
,经过定点A(0,-a)以 为方向向量的直线与经过定点B(0,a)以
为方向向量的直线与经过定点B(0,a)以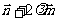 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中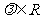
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)若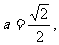 过E(0,1)的直线l交曲线C于M、N两点,求
过E(0,1)的直线l交曲线C于M、N两点,求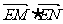 的取值范围
的取值范围
解:(Ⅰ)设P点的坐标为(x,y),则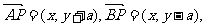
又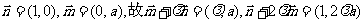
由题知向量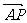 与向量
与向量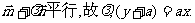
又向量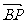 与向量
与向量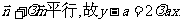
两方程联立消去参数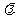 ,得点P(x,y)的轨迹方程是
,得点P(x,y)的轨迹方程是
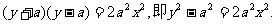
(Ⅱ)∵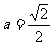 ,故点P的轨迹方程为
,故点P的轨迹方程为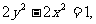
此时点E(0,1)为双曲线的焦点
①若直线l的斜率不存在,其方程为x=0,
l与双曲线交于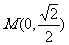 、
、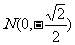 ,
,
此时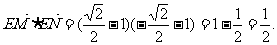
②若直线l的斜率存在,设其方程为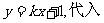
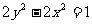 化简得
化简得
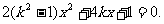
∵直线l与双曲线交于两点,
∴△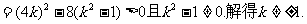
设两交点为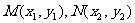 ,
,
则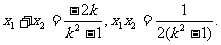
此时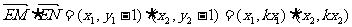
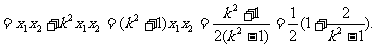
当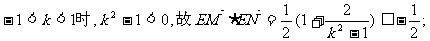
当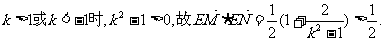
综上所述,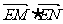 的取值范围是
的取值范围是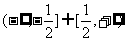
◆提炼方法:
1.交轨法也是求轨迹方程的一种重要方法,具体过程是:
(1).建立动直线(或曲线)的方程;
(2).消去动直线(或曲线)方程中的参数,得到交点(即动点)坐标x,y的方程即为所求.
6.解:点参数法 设A(0,t),B(0,3t),则P(t2/2 +1, t),
设A(0,t),B(0,3t),则P(t2/2 +1, t),
设Q(x,y),则有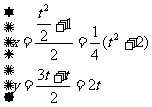 ,消去t得:y2=16(x–
,消去t得:y2=16(x– )
)
5.解:设P(x,y),则M(2x,0),N(0,2y),由AM⊥AN得方程2ax+2by-a2-b2=0.
6. 垂直于y轴的直线与y轴及抛物线y2=2(x–1)分别交于点A和点P,点B在y轴上且点A分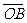 的比为1:2,求线段PB中点的轨迹方程。
的比为1:2,求线段PB中点的轨迹方程。
简答:1-4.CCBA;
5.过定点A(a,b)的两直线 l1与 l2互相垂直,设l1交x轴于点M,l2交y轴于点N,则线段MN的叫点P的轨迹方程是__________
4.(2005重庆)若动点(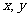 )在曲线
)在曲线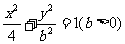 上变化,则
上变化,则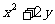 的最大值为 ( )
的最大值为 ( )
A. B.
B.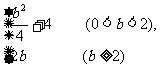
C.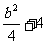 D.2
D.2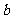
3.(2006四川)已知两定点A(-2,0),B(1,0),如果动点P满足条件|PA|=2|PB|则点P的轨迹所包围的图形的面积等于 ( . )
A.π B.4π C.8π D.9π
2.方程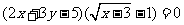 表示的曲线形状是 ( )
表示的曲线形状是 ( )
A.直线2x+3y-5=0和直线x=4 B. 直线2x+3y-5=0和射线x=4
C. 直线2x+3y-5=0(x>3)和直线x=4 D. 直线2x+3y-5=0和曲线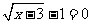
1.曲线C的方程是f(x,y)=0, 点P(x0,y0)不在曲线C上,则方程f(x,y)+f(x0,y0)=0表示的曲线与曲线C的关系是 ( )
A.有一个交点 B.有无穷多个交点 C.无交点 D.上述三种情况都有可能
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com