
1、(江苏省启东中学高三综合测试三)将抛物线y2=4x沿向量a平移得到抛物线y2-4y=4x,则向量a为
A.(-1,2) B.(1,-2) C.(-4,2) D.(4,-2) 答案:A
10.(2004春安徽)已知k>0,直线l1:y=kx,l2:y=-kx.
(1)证明:到l1、l2的距离的平方和为定值a(a>0)的点的轨迹是圆或椭圆;
(2)求到l1、l2的距离之和为定值c(c>0)的点的轨迹.
(1)证明:设点P(x,y)为动点,则
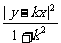 +
+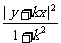 =a,
=a,
整理得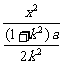 +
+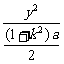 =1.
=1.
因此,当k=1时,动点的轨迹为圆;
当k≠1时,动点的轨迹为椭圆.
(2)解:设点P(x,y)为动点,则
|y-kx|+|y+kx|=c .
.
当y≥k|x|时,y-kx+y+kx=c ,
,
即y=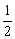 c
c ;
;
当y≤-k|x|时,kx-y-y-kx=c ,即y=-
,即y=-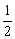 c
c ;
;
当-k|x|<y<k|x|,x>0时,kx-y+y+kx=c ,即x=
,即x=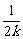 c
c ;
;
当-k|x|<y<k|x|,x<0时,y-kx-y-kx=c ,即x=-
,即x=-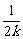 c
c .
.
综上,动点的轨迹为矩形.
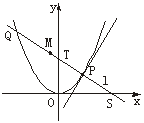
[探索题](2004福建)如下图,P是抛物线C:y=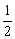 x2上一点,直线l过点P且与抛物线C交于另一点Q.若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程.
x2上一点,直线l过点P且与抛物线C交于另一点Q.若直线l与过点P的切线垂直,求线段PQ中点M的轨迹方程.
分析:欲求PQ中点M的轨迹方程,需知P、Q的坐标.思路一,P、Q是直线l与抛物线C的交点,故需求直线l的方程,再与抛物线C的方程联立,利用韦达定理、中点坐标公式可求得M的轨迹方程;思路二,设出P、Q的坐标,利用P、Q的坐标满足抛物线C的方程,代入抛物线C的方程相减得PQ的斜率,利用PQ的斜率就是l的斜率,可求得M的轨迹方程.
解:设P(x1,y1)、Q(x2,y2)、M(x0,y0),依题意知x1≠0,y1>0,y2>0.
 由y=
由y=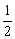 x2, ①
x2, ①
得y′=x.
∴过点P的切线的斜率k切=x1,
∴直线l的斜率kl=-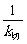 =-
=-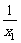 ,
,
直线l的方程为y-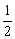 x12=-
x12=-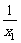 (x-x1). ②
(x-x1). ②
方法一:联立①②消去y,得x2+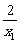 x-x12-2=0.
x-x12-2=0.
∵M为PQ的中点,
|
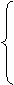 x0=
x0=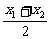 =-
=-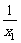 ,
,
y0=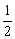 x12-
x12-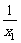 (x0-x1).
(x0-x1).
消去x1,得y0=x02+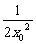 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+ +1(x≠0).
+1(x≠0).
方法二:由y1=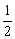 x12,y2=
x12,y2=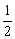 x22,x0=
x22,x0=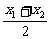 ,
,
得y1-y2=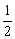 x12-
x12-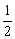 x22=
x22=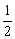 (x1+x2)(x1-x2)=x0(x1-x2),
(x1+x2)(x1-x2)=x0(x1-x2),
则x0= =kl=-
=kl=-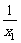 ,∴x1=-
,∴x1=-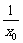 .
.
将上式代入②并整理,得y0=x02+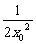 +1(x0≠0),
+1(x0≠0),
∴PQ中点M的轨迹方程为y=x2+ +1(x≠0).
+1(x≠0).
9. 设直线x─y=4a与抛物线y2=4ax 交于两点A,B (a为定值),C为抛物线上任意一点,求ΔABC的重心的轨迹方程
分析:A,B是定点,影响ΔABC的重心运动的因素是抛物线上的动点C,故选C点的坐标作参数
解:设ΔABC的重心为G(x,y) ,点C的坐标为C(x0,y0),A(x1,y1), B(x2,y2)
由方程组: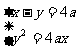 消去y并整理得:
消去y并整理得:
x2─12ax+16a2=0
∴x1+x2=12a, y1+y2=(x1─4a)+(x2─4a)=(x1+x2)─8a=4a
由于G(x,y)为ΔABC的重心,
∴
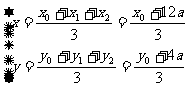 ,
,
∴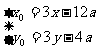 , 又点C(x0,y0)在抛物线上,
, 又点C(x0,y0)在抛物线上,
∴将点C的坐标代入抛物线的方程得:
(3y─4a)2=4a(3x─12a), 即(y─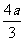 )2 =
)2 = 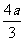 (x─4a)
(x─4a)
又点C与A,B不重合,∴x ¹ (6±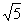 )a
)a
8. AB是圆O的直径,且|AB|=2a,M为圆上一动点,作MN⊥AB,垂足为N,在OM上取点P,使|OP|=|MN|,求点P的轨迹.
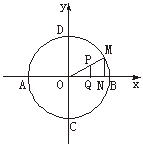 解:以圆心O为原点,AB所在直线为x轴建立直角坐标系(如下图),则⊙O的方程为x2+y2=a2,设点P坐标为(x,y),并设圆与y轴交于C、D两点,作PQ⊥AB于Q,则有
解:以圆心O为原点,AB所在直线为x轴建立直角坐标系(如下图),则⊙O的方程为x2+y2=a2,设点P坐标为(x,y),并设圆与y轴交于C、D两点,作PQ⊥AB于Q,则有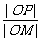 =
= .
.
∵|OP|=|MN|,
∴|OP|2=|OM|·|PQ|.
∴x2+y2=a|y|,即
x2+(y±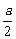 )2=(
)2=(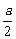 )2.
)2.
轨迹是分别以CO、OD为直径的两个圆.
7. 已知抛物线C:y=─x2+mx─1,点A(3,0),B(0,3),若抛物线C与线段AB有两个交点,求m的取值范围
先分析如下解法:线段AB所在的直线方程是x+y=3,由方程组:
 (1)
(1)
消去y得: x2─(m+1)x+4=0 (2) ,
设f(x)= x2─(m+1)x+4, 由于抛物线与线段AB有两个不同交点,
故方程f(x)=0在区间[0,3]上有两个不同根,
∴  ∴ 3<m£10/3
∴ 3<m£10/3
点评:解析几何中的轨迹方程,范围问题,都涉及等价性,即充要条件的概念
6.解:设A(x0,y0),
∵tanB+tanC=3,
∴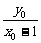 -
-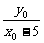 =3,点A的轨迹方程为
=3,点A的轨迹方程为
y0=-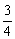 (x02-6x0+5)(x0≠1且x0≠5).
(x02-6x0+5)(x0≠1且x0≠5).
若G(x,y)为△ABC的重心,则由重心坐标公式:
x=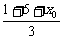 ,y=
,y= ,∴x0=3x-6,且y0=3y.
,∴x0=3x-6,且y0=3y.
代入A点轨迹方程得G的轨迹方程为
y-1=-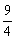 (x-3)2(x≠
(x-3)2(x≠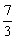 且x≠
且x≠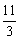 ).
).
答案:y-1=-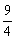 (x-3)2(x≠
(x-3)2(x≠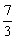 且x≠
且x≠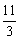 )
)
[解答题]
5.解:|BC|+|CA|=4>2,由椭圆的定义可知,点C的轨迹是以A、B为焦点的椭圆,其长轴为4,焦距为2, 短轴长为2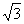 ,
,
∴椭圆方程为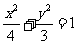 ,
,
又a>b, ∴点C在y轴左侧,必有x<0,而C点在x轴上时不能构成三角形,故x≠─2,
因此点C的轨迹方程是: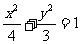 (─2<x<0)
(─2<x<0)
6.已知△ABC中,B(1,0)、C(5,0),点A在x轴上方移动,且tanB+tanC=3,则 △ABC的重心G的轨迹方程为________________.
简答.提示:1-3.ACA; 4.y= -2x2-3
5. 已知ΔABC中,ÐA,ÐB,ÐC所对应的边为a,b,c,且a>c>b,a,c,b成等差数列,|AB|=2,求顶点C的轨迹方程
4.若动点P在y=2x2+1上移动,则点P与点Q(0,-1)连线中点的轨迹方程是________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com