1. 下列各句中加点的词语，使用最恰当的一句是

A.中药是在中医学理论指导下用以防治疾病的药物，以植物为最多，也包括动物和矿物，其药效一般比较缓和。

B.虽然平时工作很忙碌，但只要有时间，我就整顿家务，让家里变得洁净、整齐、漂亮。

C.海滨公园是附近居民喜爱的运动场所，在花海中无论是散步、慢跑还是骑车锻炼都令人神气十足。

D.诗评家所谓“老杜饥寒而悯人饥寒者也”，跟白居易“饱暖而悯人饥寒者也”是不同的，饥寒让杜甫刻骨铭心，所以他写出的诗句更加深刻感人。

[答案]D

[解析]A中“药效”和“缓和”不搭配，应用“缓慢”。B中“整顿”和“家务”也不搭配，“家务”是“家庭事务”，自然不能整顿。只能“操持家务”。C中“神气十足” 形容摆出一副自以为高人一等而了不起的样子。带有傲慢的神气，而语境是“神定气闲”。

160. 把正方形ABCD沿对角线AC折成直二面角B-AC-D，E、F分别为AD、BC的中点，O为正方形的中心，求折起后∠EOF的大小

证明：过F作FM⊥AC于M，过E作EN⊥AC于N，则M，N分别为OC、AO的中点

解析：

158. 设△ABC内接于⊙O，其中AB为⊙O的直径，PA⊥平面ABC。

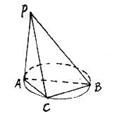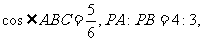　 如图求直线PB和平面PAC所成角的大小

　 159. 如图，在正方体ABCD-A₁B₁C₁D₁中，已知P，Q，R，S分别为棱A₁D₁，A₁B₁，AB，BB₁的中点，求证：平面PQS⊥平面B₁RC.(12分)

证明：连结BC₁交B₁C于O，则O为BC₁的中点

连结RO，AC₁，∵R是AB的中点　 ∴RO∥AC₁

∵P,Q分别为A₁D₁，A₁B₁的中点，易知A₁C₁⊥PQ

∴AC₁⊥PQ(三垂线定理)

157.已知△BCD中，∠BCD=90°，BC=CD=1，AB⊥平面BCD，

∠ADB=60°，E、F分别是AC、AD上的动点，且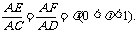

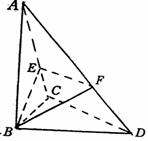　 　　 (Ⅰ)求证：不论λ为何值，总有平面BEF⊥平面ABC；

　　 (Ⅱ)当λ为何值时，平面BEF⊥平面ACD？

证明：(Ⅰ)∵AB⊥平面BCD， ∴AB⊥CD，

　　　 ∵CD⊥BC且AB∩BC=B， ∴CD⊥平面ABC.………………………………3分

　　　 又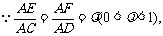

　　　 ∴不论λ为何值，恒有EF∥CD，∴EF⊥平面ABC，EF平面BEF,

　　　 ∴不论λ为何值恒有平面BEF⊥平面ABC

(Ⅱ)由(Ⅰ)知，BE⊥EF，又平面BEF⊥平面ACD，

∴BE⊥平面ACD，∴BE⊥AC.………………8分

∵BC=CD=1，∠BCD=90°，∠ADB=60°，

∴

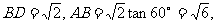
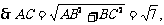由AB²=AE·AC 得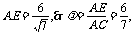

故当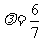时，平面BEF⊥平面ACD.………………………………………………12分

156. 有一矩形纸片ABCD，AB=5，BC=2，E，F分别是AB，CD上的点，且BE=CF=1，把纸片沿EF折成直二面角．

(1)求BD的距离；

(2)求证AC，BD交于一点且被这点平分．

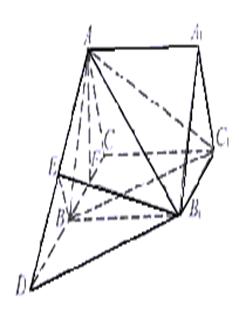
解析：将平面BF折起后所补形成长方体AEFD-A₁BCD₁，则BD恰好是长方体的一条对角线．

(1)解：因为AE，EF，EB两两垂直，

所以BD恰好是以AE，EF，EB为长、宽、高的长方体的对角线，

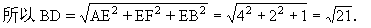．．．．．．．．．．．．．．．．6分

(2)证明：因为AD EF，EF BC，所以AD BC．

所以ACBD在同一平面内，

且四边形ABCD为平行四边形．

所以AC、BD交于一点且被这点平分

155. 已知空间四边形ABCD的边长都是1，又BD=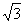，当三棱锥A-BCD的体积最大时，求二面角B-AC-D的余弦值．

解析：如图，取AC中点E，BD中点F，由题设条件知道

(1)BED即二面角B-AC-D的平面角．．．．．．．．．．．．．．．．．．．．．．．．．．．．3分

(2)当AF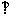面BCD时，V_A-BCD达到最大．．．．．．．．．．．．．．．．．．．．．．．．．．．．．6分

这时ED²=AD²-AE²=1-AE²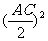=1-=1-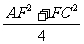

=1-，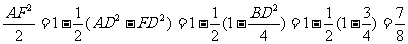

又 BE²=ED²，

∴ cos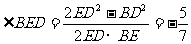．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．．12分

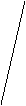
　　 　　　　　　　　　　 　　　 A　　　　　　

　　 　　　　　　　E

B　　 　　　　 F　　　 　　　　D　　　

　　 　　　　　　　　C

153. 已知矩形ABCD的边AB=1，BC=a，PA⊥平面ABCD，PA=1，问

　 BC边上是否存在点Q，使得PQ⊥QD，并说明理由.

解析：连接AQ，因PA⊥平面ABCD，所以PQ⊥QDAQ⊥QD，即以AD为直经的圆与BC有交点．

当AD=BC=aAB=1,即a1时，在BC边上存在点Q，使得PQ⊥QD；．．．．．．．．．5分

当0<a<1时，在BC边上不存在点Q，使得PQ⊥QD．．．

　 154. 如图，正三棱柱ABC-A₁B₁C₁的底面边长的3，侧棱AA₁=D是CB延长线上一点，且BD=BC.

　 (Ⅰ)求证：直线BC₁//平面AB₁D；

　 (Ⅱ)求二面角B₁-AD-B的大小；

　 (Ⅲ)求三棱锥C₁-ABB₁的体积.

(Ⅰ)证明：CD//C₁B₁，又BD=BC=B₁C₁， ∴ 四边形BDB₁C₁是平行四边形， ∴BC₁//DB₁.

又DB₁平面AB₁D，BC₁平面AB₁D，∴直线BC₁//平面AB₁D.．．．．．．．．．．．．．．．．．．．5分

(Ⅱ)解：过B作BE⊥AD于E，连结EB₁， ∵B₁B⊥平面ABD，∴B₁E⊥AD ，

∴∠B₁EB是二面角B₁-AD-B的平面角，　 ∵BD=BC=AB， ∴E是AD的中点，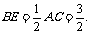

在Rt△B₁BE中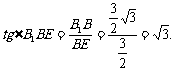，∴∠B₁EB=60°。即二面角B₁-AD-B的大小为60°…………10分

(Ⅲ)解法一：过A作AF⊥BC于F，∵B₁B⊥平面ABC，∴平面ABC⊥平面BB₁C₁C，

∴AF⊥平面BB₁C₁C，且AF=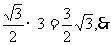

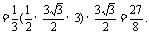　即三棱锥C₁-ABB₁的体积为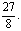…………15分

　 解法二：在三棱柱ABC-A₁B₁C₁中，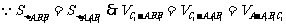

　　　　 即为三棱锥C₁-ABB₁的体积．

152. 与正方形各面成相等的角且过正方体三个顶点的截面的个数是________．

解析：如图中，截面ACD₁和截面ACB₁均符合题意要求，这样的截面共有8个；

22. 请以“推挤”为题，写一篇不少于800字的记叙文或议论文。