
引导学生通过主动参与、合作探讨学习知识
本节课采用探究教学法,通过“猜想,验证,证明”来探究二元一次不等式(组)表示的平面区域,并通过讲练结合巩固所学的知识。使用多媒体辅助教学。
重点:二元一次不等式(组)表示的平面区域
难点:寻求二元一次不等式(组)表示的平面区域
3.情感态度与价值观目标:
(1)通过学生的主动参与、学生的合作交流,培养学生的探索方法与精神;
(2)体会数学的应用价值;
(3)体会由一般到特殊,由特殊到一般的思想。
2.过程与方法目标:
(1)增强学生数形结合的思想;
(2)理解数学的转化思想,提高分析问题、解决问题的能力。
1.知识与技能目标:
(1)理解“同侧同号”并掌握不等式区域的判断方法;
(2)能作出二元一次不等式(组)表示的平面区域。
在探求“同侧同号”教学过程中,与教材处理不同的是在验证完猜想后,我引导同学们得到了其严格的逻辑证明。这样做主要基于以下几点的考虑:(1)根据学生的状况,过点P做坐标轴垂线的这种证法学生还是可以探求到,并理解和接受的。(2)在这个过程鼓励学生继续大胆的想象,合理的论证;培养学生运用联系转化的方法来处理新问题的数学思维方法。(3)让学生经历了一个数学问题的完整的探究过程“猜想、验证、证明”,以及由特殊到一般的升华。同时考虑到学生的接受能力,关于“向量内积”的证明方法,在引导学生考虑到“垂线联系”的方式后并没有展开,而是让学生在课下结合书上的证明继续探究。
二元一次不等式(组)表示的平面区域
同侧同号 证明过程(图像) 例1:
判断方法
|
教学 过程 |
教学内容 |
教学活动 |
设计说明 |
|
新 课 引 入 |
问题:营养学家指出,成人的日常饮食应该摄入至少0.075kg碳水化合物,0.06kg蛋白质,0.06kg脂肪。已知1kg食物A含有0.15kg碳水化合物,0.06kg蛋白质,0.12kg脂肪;已知1kg食物B含有0.15kg碳水化合物,0.12kg蛋白质,0.06kg脂肪。设x,y分别为每天需要食物A,B的数量(单位:千克),请列出满足营养学家日常饮食要求的数学关系式。 |
学生列出满足要求的数学关系式。 教师结合学生列出的关系式给出二元一次不等式和二元一次不等式组的概念。 |
从实际问题出发,引出二元一次不等式和二元一次不等式组的概念。体现应用价值,吸引学生的学习兴趣。 |
|
探 求 二 元 一 次 不 等 式 解 集 的 几 何 意 义 |
1.介绍开半平面和闭半平面的定义。 2.引导1:二元一次方程在直角坐标系中的图像是一条直线,那么二元一次不等式在直角坐标平面上表示什么区域? 引导2:直线将平面分成两部分,这与两个二元一次不等式  有什么关联? 有什么关联?引导3:如何验证我们的猜想? 3. 选择直线 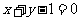 ,在平面上选择一点 ,在平面上选择一点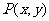 ,观察其在每一侧区域运动时, ,观察其在每一侧区域运动时, 的正负符号。 的正负符号。4.证明:在直线 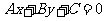 的同一侧任取一点 的同一侧任取一点 的坐标使式子 的坐标使式子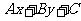 的值具有相同的符号。 的值具有相同的符号。 |
教师给出相关的一些定义后,引导学生研究二元一次不等式在直角坐标平面上表示的平面区域。 教师提出问题,引导学生思考,回答问题,进行合理的猜想:“同侧同号”。 学生给出验证方法,教师通过多媒体进行演示,验证猜想。 教师引导学生运用联系、转化的方法将点  与直线上的点联系起来,学生讨论得到证明方法,完成对于猜想的逻辑证明。 与直线上的点联系起来,学生讨论得到证明方法,完成对于猜想的逻辑证明。 |
在给出相关定义后在研究其所表示的平面区域,顺理成章,符合学生的认知规律。 采用类比推理的方法,进入本堂课的主要内容,使学生比较容易的产生相关联想。鼓励学生进行大胆的猜想,培养他们的想象能力和创新能力。 在由了想法后,自然的要对其进行验证,验证猜想的对于错。 通过验证发现可能成立,作为数学问题自然要考虑其是否可以逻辑证明,这体现了数学的严谨性。同时证明过程中渗透联系、转化的数学方法。 通过这样的探究过程加深了学生对于数学本质的理解,更重要的是让学生经历了知识形成的一个完整过程,这培养了他们解决问题的思维方法。 |
|
画平 面区 域的 方法 |
画平面区域的方法 方法一:直线定界,特殊点定域 方法二:看A:右同左异; 看B:上同下异。 |
教师引导学生依据“同侧同号”的结论和证明过程总结得出画平面区域的方法。 学生得出并完善方法。 |
培养学生解决问题的能力,加强他们总结归纳形成方法的能力。 让学生体会到由一般到特殊,再由特殊回归到一般的认识问题的方法。 |
|
方 法 应 用 |
例1:画出下面二元一次不等式表示的平面区域: (1) 2x- y- 3>0; (2) 3x+ 2y- 6≤0. 例2:画出引例中的二元一次不等式组  表示的平面区域。 表示的平面区域。例3:写出表示下面平面区域的二元一次不等式组:(包括三角形的三条边) 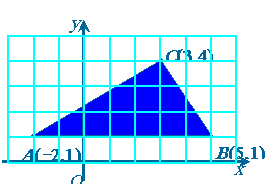  |
例1学生板书画出不等式的平面区域,并讲解画出的过程和判断区域的方法。 教师强调边界线虚实线的划法。 例2教师点拨学生在作出每个区域后找出它们的交集。 学生作图,教师展示其中较好的作图。 例3由教师引导,学生完成。 |
通过例题进一步理解和巩固所学的判断方法,掌握画出二元一次不等式(组)表示的区域的判断方法。 与引例相呼应,彻底的解决该问题,通过应用题,让学生体会到数学的应用价值。 由二元一次不等式到不等式组的设计,由浅入深,由易到难,便于学生的接受。 从相反的方向对于知识进行练习,加深学生对于知识与方法的理解与运用。 |
|
归 纳 小 结 |
(1)二元一次不等式表示的平面区域; (2)数形结合的方法; (3)猜想,验证,逻辑证明的研究问题的方法。 |
师生共同回顾与总结所学的知识与方法。 |
通过知识与方法的总结,使得所学的知识系统化、条理化。 |
|
课 堂 作 业 |
作业: 1.P89页第3题; 2.研究P88页探索与研究。 |
教师批阅,发现问题及时纠正。 |
根据学生情况分层设计,注重学生的差异。 探索与研究,增强学生课下的自学与交流意识。 |
2.学法设计
在学习中,让其以主体的态度,而不是被动的接受。经历知识的形成和发展过程,通过观察、归纳、思考、探索、交流、反思参与学习,认识和理解数学知识,学会学习,发展能力。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com