
2.若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)>0,则f(x)在区间(a,b)内就一定没有零点么?
1.若函数y=f(x)在区间[a,b]上连续,且f(a)·f(b)<0,则f(x)在区间(a,b)内会是只有一个零点么?
[环节一:揭示意义,明确目标]揭示本章意义,指明课节目标
教师活动:用屏幕显示第三章 函数的应用
3.1.1方程的根与函数的零点
教师活动:这节课我们来学习第三章函数的应用。通过第二章的学习,我们已经认识了指数函数、对数函数、幂函数、分段函数等函数的图象和性质,而这一章我们就要运用函数思想,建立函数模型,去解决现实生活中的一些简单问题。为此,我们还要做一些基本的知识储备。方程的根,我们在初中已经学习过了,而我们在初中研究的“方程的根”只是侧重“数”的一面来研究,那么,我们这节课就主要从“形”的角度去研究“方程的根与函数零点的关系”。
教师活动:板书标题(方程的根与函数的零点)。
[环节二:巧设疑云,轻松渗透]设置问题情境,渗透数学思想
教师活动:请同学们思考这个问题。用屏幕显示判断下列方程是否有实根,有几个实根?
(1)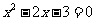 ;(2)
;(2)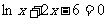 .
.
学生活动:回答,思考解法。
教师活动:第二个方程我们不会解怎么办?你是如何思考的?有什么想法?我们可以考虑将复杂问题简单化,将未知问题已知化,通过对第一个问题的研究,进而来解决第二个问题。对于第一个问题大家都习惯性地用代数的方法去解决,我们应该打破思维定势,走出自己给自己画定的牢笼!这样我们先把所依赖的拐杖丢掉,假如第一个方程你不会解,也不会应用判别式,你要怎样判断其实根个数呢?
学生活动:思考作答。
教师活动:用屏幕显示函数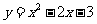 的图象。
的图象。
学生活动:观察图像,思考作答。
教师活动:我们来认真地对比一下。用屏幕显示表格,让学生填写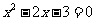 的实数根和函数图象与x轴的交点。
的实数根和函数图象与x轴的交点。
学生活动:得到方程的实数根应该是函数图象与x轴交点的横坐标的结论。
教师活动:我们就把使方程成立的实数x称做函数的零点.
[环节三:形成概念,升华认知]引入零点定义,确认等价关系
教师活动:这是我们本节课的第一个知识点。板书(一、函数零点的定义:对于函数y=f(x),使方程f(x)=0的实数x叫做函数y=f(x)的零点)。
教师活动:我可不可以这样认为,零点就是使函数值为0的点?
学生活动:对比定义,思考作答。
教师活动:结合函数零点的定义和我们刚才的探究过程,你认为方程的根与函数的零点究竟是什么关系?
学生活动:思考作答。
教师活动:这是我们本节课的第二个知识点。板书(方程的根与函数零点的等价关系)。
教师活动:检验一下看大家是否真正理解了这种关系。如果已知函数y=f(x)有零点,你怎样理解它?
学生活动:思考作答。
教师活动:对于函数y=f(x)有零点,从“数”的角度理解,就是方程f(x)=0有实根,从“形”的角度理解,就是图象与x轴有交点。从我们刚才的探究过程中,我们知道,方程f(x)=0有实根和图象与x轴有交点也是等价的关系。所以函数零点实际上是方程f(x)=0有实根和图象与x轴有交点的一个统一体。
在屏幕上显示:函数y=f(x)有零点
方程f(x)=0有实数根 函数y=f(x)的图象与x轴有交点
函数y=f(x)的图象与x轴有交点
教师活动:下面就检验一下大家的实际应用能力。
[环节四:应用思想,小试牛刀]数学思想应用,基础知识强化
教师活动:用屏幕显示求下列函数的零点.
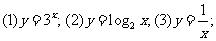
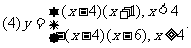
 学生活动:由四位同学分别回答他们确定零点的方法。画图象时要求用语言描述4个图象的画法;
学生活动:由四位同学分别回答他们确定零点的方法。画图象时要求用语言描述4个图象的画法;
教师活动:根据学生的描述,在黑板上作出图象(在接下来探究零点存在性定理时,图象会成为同学们思考问题的很好的参考)。
教师活动:我们已经学习了函数零点的定义,还学习了方程的根与函数零点的等价关系,在这些知识的探究发现中,我们也有了一些收获,那我们回过头来看看能不能解决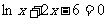 的根的存在性问题?
的根的存在性问题?
学生活动:可受到化归思想的启发应用数形结合进行求解。
教师活动:用屏幕显示学生所论述的解题过程。这种解法充分运用了我们前面的解题思想,将未知问题转化成已知问题,将一个图象不会画的函数转化成了两个图象都会画的函数,利用两个函数图象的交点解决实根存在性问题。看来我们的探究过程是非常有价值的。
教师活动:如果不转化,这个问题就真的解决不了么?现在最棘手的问题是y= 的图象不会画,那我们能不能不画图象就判断出零点的存在呢?
的图象不会画,那我们能不能不画图象就判断出零点的存在呢?
[环节五:探究新知,思形想数]探究图象本质,数形转化解疑
教师活动:我们看到,当函数图象穿过x轴时,图象就与x轴产生了交点,图象穿过x轴这是一种几何现象,那么如何用代数形式来描述呢?用屏幕显示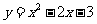 的函数图象,多次播放抛物线穿过x轴的画面。
的函数图象,多次播放抛物线穿过x轴的画面。
学生活动:通过观察图象,得出函数零点的左右两侧函数值异号的结论.
教师活动:好!我们明确一下这个结论,函数y=f(x)具备什么条件时,能在区间(a,b)上存在零点?
学生活动:得出f(a)·f(b)<0的结论。
教师活动:若f(a)·f(b)<0,函数y=f(x)在区间(a,b)上就存在零点吗?
学生活动:可从黑板上的图象中受到启发,得出只有在[a,b]上连续不断的函数,在满足f(a)·f(b)<0的条件时,才会存在零点的结论。
[环节六:归纳定理,深刻理解]初识定理表象,深入理解实质
教师活动:其实同学们无形之中已经说出了我们数学中的一个重要定理,那就是零点存在性定理。这是我们本节课的第三个知识点。板书(三、零点存在性定理)。
教师活动:用屏幕显示函数零点存在性定理:
如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a) ·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点.
即存在c∈(a,b),使得f(c)=0,这个c也就是方程f(x)=0的根.
教师活动:这个定理比较长,找个同学给大家读一下,让大家更好地体会定理的内容。
学生活动:读出定理。
教师活动:大家注意到了么,定理中,开始时是在闭区间[a,b]上连续,结果推出时却是在开区间(a,b)上存在零点。你怎样理解这种差异?
学生活动:思考作答。
教师活动:虽然我们已经得到了零点存在性定理,但同学们真的那么坦然么?结合黑板上的图象,再结合定理的叙述形式,你对定理的内容可有疑问?
学生活动:通过观察黑板上的板书图象,大致说出以下问题:
|
授课类型:新 授 课 |
教学方法:启发式教学、探究式学习 |
|
教学课件:自制Powerpoint课件 |
多媒体设备:计算机 |
|
教学重点 |
零点的概念及零点存在性的判定。 |
|
教学难点 |
探究判断函数的零点个数和所在区间的方法. |
|
知识与技能 |
1.结合方程根的几何意义,理解函数零点的定义; 2.结合零点定义的探究,掌握方程的实根与其相应函数零点之间的等价关系; 3.结合几类基本初等函数的图象特征,掌握判断函数的零点个数和所在区间的方法. |
|
过程与方法 |
1.通过化归与转化思想的引导,培养学生从已有认知结构出发,寻求解决棘手问题方法的习惯; 2.通过数形结合思想的渗透,培养学生主动应用数学思想的意识; 3.通过习题与探究知识的相关性设置,引导学生深入探究得出判断函数的零点个数和所在区间的方法; 4.通过对函数与方程思想的不断剖析,促进学生对知识灵活应用的能力。 |
|
情感、态度与价值观 |
1.让学生体验化归与转化、数形结合、函数与方程这三大数学思想在解决数学问题时的意义与价值; 2.培养学生锲而不舍的探索精神和严密思考的良好学习习惯; 3.使学生感受学习、探索发现的乐趣与成功感。 |
本节课所学内容:
三种类型的比大小及各自的方法:
本节课所用到的数学思想和方法:
思考题:(2009全国II 7)
设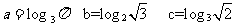 则( )
则( )
A、a>b>c B、a>c>b C、b>a>c D、b>c>a
 (1) log0.62 log0.61.9 (2) loga3 loga (a>0,a≠1)
(1) log0.62 log0.61.9 (2) loga3 loga (a>0,a≠1) 教学流程图
教学流程图



|

|

|
|
|
|


|
|
通过本节课的教学实例来看,这种通过课本内容预习,而后课堂交流学习成果的方法效果不错,既能很好的完成教学任务,又能充分发挥学生学习的主动性。在自主探究时,学生分组讨论过程中,我参与小组讨论,对有能力的小组,在探究出一种方法后,可鼓励完成更多的方法探究,对于能力较弱的小组,可给予适当的提示,使学生都能动起来,课堂都有所收获,增强学生自信。另外,对于学生的总结回答,可能会比较慢,我一定会耐心听,及时鼓励,给予学生微笑和语言的鼓励,效果很好。在小结环节中,对于高一学生自己小结的方法,是我一直的教学尝试,由于只训练了半学期,学生只能达到小结知识的程度,在以后的训练中还会加入数学思想、数学方法的小结内容,使这些数学名词让学生不再觉得抽象,而是变成具体的,可操作的、具体的解题工具。
7、 作业
包括两个方面:1、书写作业 2、下节课前的预习作业
6、 思考题
以2009高考题为例,让学生学以致用,增强数学学习兴趣。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com