
(二) 合作探究,收获新知:
1、分类变量:变量的不同“值”表示个体所属的不同类别,像这类变量称为分类变量。
2、列联表:像表1 这样列出的两个分类变量的频数表,称为列联表。(高中阶段我们只研究列联表。)
问题1:根据列联表中的数据,计算吸烟者和不吸烟者中患肺癌的比重各是多少?
3、三维柱形图和二维条形图:
将列联表中的数据输入到Excel表格中,将数据呈现到图形中。
师用Excel表格演示:借助三维柱形图和二维条形图的展示,使学生直观感觉到吸烟和患肺癌可能会有关系。
师:通过分析数据和图形,我们得到的直观印象是“吸烟和患肺癌有关”。当对这个问题作出推断时,我们不能仅凭主观意愿作出结论,那么我们是否能够以一定的把握认为“吸烟与患肺癌有关”呢?
2010.9.19
5、课后作业,学以致用
效果分析:本节课通过对典型案例的探究,学生理解了独立性检验的基本思想及其具体实施步骤。让学生从中初步体会了数学与实际生活的联系,以及怎样运用所学知识去解决实际生活中的问题。
本节课通过对几个问题的设置,经过学生之间的讨论、互评,教师的引导帮助,使得本节课的难点得以突破。学生通过总结也完善了自己的认知结构,从而对该部分得知识也有了更深的体会。
我在课堂上注重学生的主体参与,努力创设教师引导下的学生自主探究、合作交流的学习方式。通过课堂练习,看到学生基本上能掌握用独立性检验思想解决实际问题,课前制定的教学目标基本实现。
通过反思,才能进步,我觉得课前预设与课堂生成相结合,才是符合新课程理念的对学生发展最为有利的教法。
非常感谢主办单位为我们年轻教师的成长提供了这样一个平台,我会在今后努力工作,使自己快速的成长起来,也希望各位专家,评委和同行们批评指正,谢谢!
黑龙江省牡丹江市第一高级中学 张宁
4、课堂小结,感悟提高
学生进行思考后,对本节课所学知识进行梳理,教师再进行补充概括。让本节课所学的知识在学生的感悟中得以升华。
3、课堂练习,夯实基础
课上到这里,学生已掌握了独立性检验的基本步骤,练习就是进一步巩固所学知识,运用其来解决实际问题。
2、合作探究,收获新知
通过用字母表示的列联表:
表2 吸烟与肺癌列联表
|
|
不患肺癌 |
患肺癌 |
总计 |
|
不吸烟 |
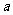 |
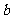 |
 |
|
吸烟 |
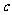 |
 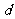 |
 |
|
总计 |
 |
 |
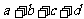 |
在假设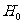 :“吸烟与患肺癌没有关系”的基础上。引导学生得出
:“吸烟与患肺癌没有关系”的基础上。引导学生得出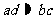 。
。
因此,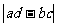 越小,说明吸烟与患肺癌之间关系越弱;
越小,说明吸烟与患肺癌之间关系越弱;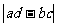 越大,说明吸烟与患肺癌之间关系越强。 (上述结论由生思考后回答。)
越大,说明吸烟与患肺癌之间关系越强。 (上述结论由生思考后回答。)
师:介绍统计学中有这样一个公式
构造一个随机变量 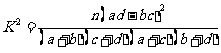 (1)
(1)
(其中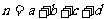 为样本容量。)
为样本容量。)
学生得出结论:若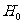 成立,即“吸烟与患肺癌没有关系”,则
成立,即“吸烟与患肺癌没有关系”,则 应该很小。
应该很小。
根据表1中的数据,利用公式(1)计算得到 的观测值为
的观测值为
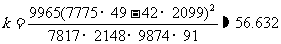
这个值到底能告诉我们什么呢?
统计学家经过研究后发现,在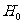 成立的情况下,
成立的情况下,
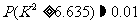 (2)
(2)
对于问题2的设计,目的是让学生理解,在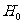 成立的情况下,
成立的情况下,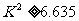 的发生的概率非常小,是一个小概率事件。
的发生的概率非常小,是一个小概率事件。
对于问题3的设计,学生讨论的很激烈,经过同学互相点评以及教师的适时引导,学生慢慢理解了当小概率事件发生时,一般认为是假设的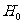 出现了问题,因此认为结论在很大的程度上是成立的。
出现了问题,因此认为结论在很大的程度上是成立的。
将独立性检验和反证法作类比,加深学生对独立性检验思想的理解。学生活动:分组进行讨论,而后让学生总结二者的区别和联系,培养学生学会用联系的观点看问题。
介绍临界值表,教学生学会运用临界值表。
总结独立性检验的基本步骤。
精心设计课堂环节,共同实现师生互动。在设计本节课的时候,我是从以下几个方面入手的。
1、创设情境,导入新课
通过对典型案例“吸烟是否对患肺癌有影响?”的提出,联系生活,引起共鸣,激发学生的学习兴趣。从生活的实例出发,让学生充分体会数学与实际生活的联系,从而使得本节知识的形成更自然、更生动。
先介绍分类变量、列联表的概念。
对于问题1的设计,是想让学生通过对列联表中数据的观察和计算,得出结论,吸烟者和不吸烟者患肺癌的可能性存在差异,吸烟者中患肺癌的可能性大。
将列联表中的数据输入到Excel表格中,将数据呈现到图形上,用计算机演示三维柱形图和二维条形图,让生观察图形,总结可以得出什么样的结论?用多种统计图使学生直观感觉两个分类变量是否有关系,然后再进行检验。
提出问题:是否能够以一定的把握认为“吸烟与患肺癌有关系”呢? 设置问题,引发学生的思考,激发学生的求知欲望。
在独立性检验中,教科书通过典型案例“吸烟是否与患肺癌有关系”的研究,介绍了独立性检验的基本思想、方法和初步应用。独立性检验的步骤是固定的,仿照教科书的例题,学生不难完成习题,但独立性检验的思想对学生来说是比较难理解的,教学中如何结合例子介绍独立性检验的思想,才能使得学生很好的理解是一个教学难点。那么,在教学过程中,采用了与反证法做类比,帮助学生理解独立性检验的思想。两者都是先假设结论不成立,然后根据是否能够推出“矛盾”来断定结论是否成立。但二者“矛盾”的含义不同,反证法中的“矛盾”是指一种不符合逻辑事情的发生;而独立性检验中的“矛盾”是指一种不符合逻辑的小概率事件的发生,即在结论不成立的假设下,推出有利于结论成立的小概率事件发生。我们知道,小概率事件在一次试验中通常是不会发生的,因此认为结论在很大的程度上是成立的。这样做了类比后,可以很好的帮助理解独立性检验的基本思想。
2、培养学生运用所学知识,依据独立性检验的思想作出合理推断的实事求是的好习惯。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com