
1.关注去年高考试题变化。
2009年化学考纲与去年相比无明显变化。但是,在2008年高考中,化学部分的命题风格有所调整,让部分考生感到难度增加,这应引起考生们的高度重视。
第一,在第Ⅱ卷试题中,以前是用实际生活中的问题来考知识,2008年高考试题则是用知识来解决实际问题,对学生运用知识的要求明显提高,但一些考生由于平时训练不够,答题时感到“力不从心”。
第二,对能力的要求有所提高。2008年高考计算能力要求提高,虽然难度不大,但一些考生感到答题时间不够。另外,考题中出现“用字母代替未知元素,然后进行推理和计算”这类题,有的考生平时未接触过,答题时感到不适,从而出现失分。
2009年高考,化学命题是继续沿用去年风格,还是回归以前的风格,目前尚不可预知。但复习时,考生还是“有备无患”为好,对2008年高考试题中的变化,应予以重视。
4.自学能力
(1)敏捷地接受试题所给出的新信息的能力;(2)将试题所给的新信息,与课内已学过的有关知识结合起来,解决问题的能力;(3)在分析评价的基础上,应用新信息的能力。
这四种能力范畴,事实上是有重叠交叉的。一个试题可以测试多种能力或是一种能力中的多个层次。
名师解读
省实验中学高三备课组组长
刘道华
3.思维能力 (1)对中学化学应该掌握的内容能融会贯通。将知识点统摄整理,使之网络化,有序地存储,有正确复述、再现、辨认的能力。(2)能将化学问题分解,找出解答的关键。能够运用自己存储的知识,将它们分解、迁移转换、重组,使问题得到解决的应用能力。(3)能将化学信息(含实际事物、实验现象、数据和各种信息、提示、暗示),按题设情境抽象归纳、逻辑地统摄成规律,并能运用此规律,进行推理(收敛和发散)的创造能力。(4)通过分析和综合、比较和论证,对解决问题的方案进行选择和评价的能力。(5)将化学问题抽象成为数学问题,利用数学工具,通过计算和推理(结合化学知识),解决化学问题的能力。
2.实验能力 (1)用正确的化学实验基本操作,完成规定的“学生实验”的能力;(2)观察记录实验现象,处理实验数据和分析实验结果,得出相应结论的能力;(3)初步处理实验过程中的有关安全问题的能力;(4)识别和绘制典型的实验仪器装置图的能力;(5)根据实验试题的要求,设计或评价简单实验方案的能力。
1.观察能力 能够通过对实验现象、实物、模型、图形、图表以及自然界、生产和生活中的化学现象的观察,获取有关的感性知识和印象,并对这些感性知识进行初步加工和记忆的能力。
(六)板书设计
|
1.2独立性检验的基本思想及其初步应用(一) |
|
一、 有关概念
二、独立性检验
三、例题: 1、 分类变量 1、独立性检验的思想 2、 列联表 2、独立性检验的步骤 |
(五)课后作业,学以至用
课本第18页 第1题和第2题
(四)课堂小结,感悟提高
知识梳理

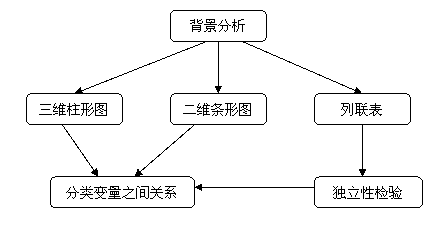

(三)课堂练习,夯实基础
1、应用举例
练习1、在某医院,因为患心脏病而住院的名男性病人中,有人秃顶,而另外名不是因为患心脏病而住院的男性病人中有人秃顶。能够以 99 %的把握认为“秃顶与患心脏病”有关系吗?
2、展望高考
本节内容为新课标中的新增内容,主要考查独立性检验的统计分析方法, 2010年宁夏理科高考试题,2009年辽宁文科高考试题均以解答题的形式考查2×2列联表及独立性检验问题,是一个新的考查方向。
思考1、(2010年新课标全国卷,宁夏,海南,吉林,黑龙江等地)
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
|
性别 是否需要志愿者 |
男 |
女 |
|
需要 |
40 |
30 |
|
不需要 |
160 |
270 |
(1) 估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2) 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
附:
|
P( |
0.050 |
0.010 |
0.001 |
|
|
3.841 |
6.635 |
10.828 |
思考2、(黑龙江省2010年高三二模试题)
某研究小组为了研究中学生的身体发育情况,在某学校随机抽出名至周岁的男生,将他们的身高和体重制成列联表,根据列联表的数据,可以有 %的把握认为该学校至周岁的男生的身高和体重之间有关系。
独立性检验临界值表
|
P( |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
5.024 |
6.635 |
7.879 |
10.828 |
独立性检验随机变量值的计算公式:(其中)
|
|
超重 |
不超重 |
合计 |
|
偏高 |
4 |
1 |
5 |
|
不偏高 |
3 |
12 |
15 |
|
合计 |
7 |
13 |
20 |
1、独立性检验的思想
把表1中的数字用字母代替,得到如下用字母表示的列联表:
表2 吸烟与肺癌列联表
|
|
不患肺癌 |
患肺癌 |
总计 |
|
不吸烟 |
|
|
|
|
吸烟 |
|
|
|
|
总计 |
|
|
|
为了回答上述问题,我们先假设:吸烟与患肺癌没有关系。
则有:,即。
因此,越小,说明吸烟与患肺癌之间关系越弱;越大,说明吸烟与患肺癌之间关系越强。
构造一个随机变量
(1)
(其中为样本容量。)
若成立,即“吸烟与患肺癌没有关系”,则应该很小。
根据表1中的数据,利用公式(1)计算得到的观测值为
这个值到底能告诉我们什么呢?
统计学家经过研究后发现,在成立的情况下,
(2)
问题2:如何理解在成立的情况下,(2)式的含义呢?
问题3:结合(2)式,以及的观测值,由这两个式子你能得到什么样的结论呢?
师:这种判断会犯错误,但犯错误的概率不会超过,即我们有的把握认为“吸烟与患肺癌有关系”。
上面这种利用随机变量来确定是否能以一定把握认为“两个分类变量有关系”的方法,称为两个分类变量的独立性检验。
类比:上面解决问题的想法类似于反证法。可以从与反证法思想比较的角度帮助学生理解上面介绍的独立性检验的思想。
下表列出了二者的对应关系:
|
反证法 |
独立性检验 |
|
要证明的结论 |
要检验的是 |
|
在A不成立的前提下进行推理 |
在不成立的条件下,即成立的条件下进行推理 |
|
推出矛盾,意味着结论成立 |
推出有利于成立的小概率事件发生,意味着成立的可能性很大 |
|
没有找到矛盾,不能对下任何结论,即反证法不成功 |
推出有利于成立的小概率事件不发生,接受原假设 |
从上面的对比中,可以看出独立性检验的思想方法和反证法类似,不同之处有两个:其一是在独立性检验中用有利于的小概率事件的发生代替了反证法中的矛盾;其二是独立性检验中的接受原假设的结论相当于反证法中没有找到矛盾。
师:要确认是否能以给定的可信程度认为“两个分类变量有关系”?(师生共同回忆上述问题的独立性检验的过程。)
怎样判断的观测值是大还是小呢?这仅需确定一个正数,如果时,就认为“两个分类变量之间有关系”;否则就认为“两个分类变量之间没有关系”.
我们称这样的为一个判断规则的临界值。
在实际应用中,要在获取样本数据之前通过下表确定临界值:
2、独立性检验的基本步骤:
① 根据实际问题需要的可信程度确定临界值;
② 利用公式(1),由观测数据计算得到随机变量的观测值;
③ 如果,就以的把握认为“与有关系”;否则就说没有的把握认为 “与有关系”。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com