
4.设二次函数y=f (x)的最小值为4,且f(0)=f(2)=6,求f(x)的解析式。
3.已知 ,则函数
,则函数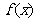 的解析式为
( )
的解析式为
( )
(A)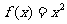 (B)
(B)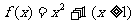
(C)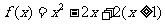 (D)
(D)
2.函数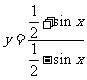 的定义域为
的定义域为
1.已知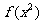 的定义域为
的定义域为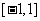 ,则
,则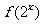 的定义域为 .
的定义域为 .
考题1(2005江苏卷)已知a,b为常数,若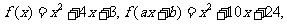 则
则 .
.
考题2(2005湖北卷)函数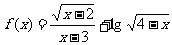 的定义域是
的定义域是
考题3(2005全国卷Ⅰ)已知二次函数 的二次项系数为
的二次项系数为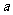 ,且不等式
,且不等式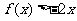 的解集为
的解集为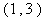 。
。
(Ⅰ)若方程 有两个相等的根,求
有两个相等的根,求 的解析式;
的解析式;
(Ⅱ)若 的最大值为正数,求
的最大值为正数,求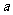 的取值范围
的取值范围
考题4(2006湖北文)设f(x)=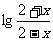 ,则
,则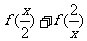 的定义域为(
)
的定义域为(
)
A. 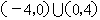 B.(-4,-1)
B.(-4,-1)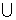 (1,4)
(1,4)
C. (-2,-1)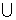 (1,2)
D. (-4,-2)
(1,2)
D. (-4,-2)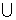 (2,4)
(2,4)
例1.已知函数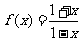 的定义域为
的定义域为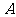 ,函数
,函数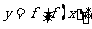 的定义域为
的定义域为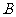 ,则
( )
,则
( )
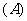
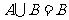
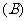
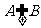
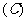
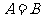
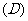
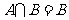
例2.(1)已知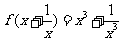 ,求
,求 ;
;
(2)已知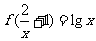 ,求
,求 ;
;
(3)已知 是一次函数,且满足
是一次函数,且满足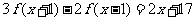 ,求
,求 ;
;
(4)已知 满足
满足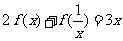 ,求
,求 .
.
例3.设函数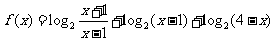 ,
,
(1)求函数的定义域;
(2)问 是否存在最大值与最小值?如果存在,请把它写出来;如果不存在,请说明理由.
是否存在最大值与最小值?如果存在,请把它写出来;如果不存在,请说明理由.
例4.已知函数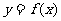 是定义在
是定义在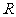 上的周期函数,周期
上的周期函数,周期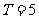 ,函数
,函数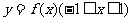 是奇函数.又知
是奇函数.又知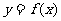 在
在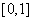 上是一次函数,在
上是一次函数,在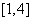 上是二次函数,且在
上是二次函数,且在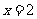 时函数取得最小值
时函数取得最小值 .
.
① 证明: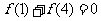 ;
;
② 求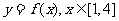 的解析式;
的解析式;
③ 求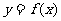 在
在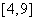 上的解析式.
上的解析式.
2.求函数定义域一般有三类问题:
(1)给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
(2)实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
(3)已知 的定义域求
的定义域求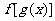 的定义域或已知
的定义域或已知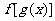 的定义域求
的定义域求 的定义域:
的定义域:
①若已知 的定义域
的定义域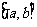 ,其复合函数
,其复合函数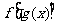 的定义域应由
的定义域应由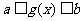 解出;
解出;
②若复合函数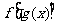 的定义域为
的定义域为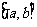 ,则
,则 的定义域为
的定义域为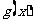 在
在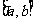 上的值域.
上的值域.
1.求函数解析式的题型有:
(1)已知函数类型,求函数的解析式时常用待定系数法;
(2)已知 求
求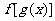 或已知
或已知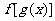 求
求 :换元法、配凑法;
:换元法、配凑法;
(3)应用题求函数解析式常要根据实际问题的意义来布列函数关系,确定函数的定义域.
(二)有人试图利用细菌的抗病毒基因对不抗病大豆进行遗传改良,以获得抗病大豆品种。
(6)构建含外源抗病毒基因的重组DNA分子时,使用的酶有______________________。
(7)判断转基因大豆遗传改良成功的标准是__________________________________,具体的检测方法_______________________________________________________________。
(一)大豆子叶颜色(BB表现深绿;Bb表现浅绿;bb呈黄色,幼苗阶段死亡)和花叶病的抗性(由R、r基因控制)遗传的实验结果如下表:
|
组合 |
母本 |
父本 |
F1的表现型及植株数 |
|
一 |
子叶深绿不抗病 |
子叶浅绿抗病 |
子叶深绿抗病220株;子叶浅绿抗病217株 |
|
二 |
子叶深绿不抗病 |
子叶浅绿抗病 |
子叶深绿抗病110株叶深绿不抗病109株; 子叶浅绿抗病108株;子叶浅绿不抗病113株 |
(1)组合一中父本基因型是___________,组合二中父本基因型是_____________。
(2)用表中F1的子叶浅绿抗病植株自交,在F2的成熟植株中,表现型的种类有_____________
__________________________________________________,其比例为_____________。
(3)用子叶深绿与子叶浅绿植株杂交得F1,F1随机交配得到的F2成熟群体中,B基因的基因频率为________________。
(4)将表中F1的子叶浅绿抗病植株的花粉培养成单倍体植株,再将这些植株的叶肉细胞制成不同的原生质体。如要得到子叶深绿抗病植株,需要用_________________基因型的原生质体进行融合。
(5)请选用表中植物材料设计一个杂交育种方案,要求在最短的时间内选育出纯合的子叶深绿抗病大豆材料。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com