8.诱导公式

α+2kπ(k∈Z)、－α、π±α、2π－α的三角函数值，等于α的同名函数值，前面加上一个把α看成锐角时原函数值的符号.--函数名不变，符号看象限。

另外：sin(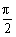－α)=cosα，cos(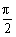－α)=sinα.--函数名改变。

7.同角三角函数关系式:

sin²α+cos²α=1(平方关系)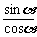；=tanα(商数关系)；tanαcotα=1(倒数关系).

6. 任意角三角函数的定义:在角α的终边上任意一点P(x，y)与原点的距离是r(r=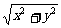＞0)，则sinα=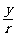，cosα=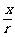，tanα=.

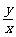三角函数两件事:一是符号,二是比值,且比值与P上在终边上的位置无关.

5．弧长公式:;　 扇形的面积公式： 。

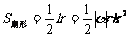4．弧度与角度的换算：180⁰=π(弧度)，1弧度=(180/π)⁰≈57⁰18＇。

3．弧度制: 规定

(1)等于半径长的弧所对的圆心角叫做一弧度的角,作为弧度制的单位;

(2) 任一已知角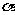的弧度数的绝对值。

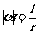(3)　　 正角的弧度数为正数，负角的弧度数为负数，零角的弧度数为零。

这种以“弧度”作为单位来度量角的制度叫做弧度制。

比值l/r与所取圆的半径大小无关，而仅与角的大小有关。

2.角在直角坐标系中的表示：角的顶点在原点，始边在x轴的非负半轴上.

(1) 象限角:角的终边在第几象限，就说这个角是第几象限的角。

(2) 象间角:角的终边在坐标轴上，就说这个角不属于任何象限，它叫象间角。

(3)　 与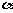角终边相同的角的集合：{β|β=k360°+α,k∈Z}

终边相同的角不一定相等，终边相同的角有无数多个，它们相差360°的整数倍。

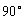(4) 正确理解：“间的角” “第一象限的角”，“锐角”，“小于的角”，这四种角的集合分别表示为：

，

，　　 。

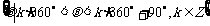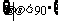1．　 角的定义：一条射线绕着端点从一个位置旋转到另一个位置所成的图形。

角按其旋转方向可分为：正角，零角，负角。

2.掌握任意角的三角函数概念、符号、同角三角函数公式和诱导公式;

1.熟悉任意角的概念、弧度制与角度制的互化、弧度制下的有关公式;