
1. 依次填入下列序号处的标点符号,正确的一项是
乐观、自信,是金晶留给人们最深的印象1我从小性格就像个男孩子,记得那时很爱看电影《佐罗》2看完后就觉得自己真的成了那里面的剑客3这位被大学生称作“微笑天使”的姑娘笑着说4后来在2001年我很自然地选择了学习击剑5
|
|
1 |
2 |
3 |
4 |
5 |
|
A |
。“ |
,, |
。” |
,“ |
。” |
|
B |
,“ |
, |
。” |
:“ |
。” |
|
C |
。“ |
, |
”。 |
,“ |
”。 |
|
D |
,“ |
。 |
”。 |
:“ |
”。 |
[答案]A
[解析]本题考查正确使用标点符号,主要考查“某某说”位于中间时前后的标点情况。①后的“我”表明下文是金晶自己说的话,③后出现“金晶”表明是说这话的状态。④后又出现了“我”,表明仍然是金晶的话。所以③前应该用引号,③后应该用逗号引号。文中说的话是独立引用,标点在引号之内。
300. 已知四面体A-BCD,AO1⊥平面BCD,且O1为ΔBCD的垂心.BO2⊥平面ACD,求证:O2是ΔACD的垂心.
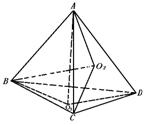
证明 如图所示,连结BO1,AO2,
∵AO1⊥平面BCD,O1为ΔBCD的垂心,
∴BO1⊥CD,由三垂线定理得AB⊥CD.
又BO2⊥平面ACD,由三垂线逆定理得AO2⊥CD.
同理连结DO1,CO2可证BC⊥AD,即CO2⊥AD.
∴O2是ΔACD垂心.
299. 已知矩形ABCD,过A作SA⊥平面AC,再过A作AE⊥SB交SB于E,过E作EF⊥SC交SC于F
(1)求证:AF⊥SC
(2)若平面AEF交SD于G,求证:AG⊥SD

解析: 如图,欲证AF⊥SC,只需证SC垂直于AF所在平面,即SC⊥平面AEF,由已知,欲证SC⊥平面AEF,只需证AE垂直于SC所在平面,即AE⊥平面ABC,再由已知只需证AE⊥BC,而要证AE⊥BC,只需证BC⊥平面SAB,而这可由已知得证
证明 (1)∵SA⊥平面AC,BC 平面AC,∴SA⊥BC
平面AC,∴SA⊥BC
∵矩形ABCD,∴AB⊥BC
∴BC⊥平面SAB
∴BC⊥AE又SB⊥AE ∴AE⊥平面SBC
∴SC⊥平面AEF
∴AF⊥SC
(2)∵SA⊥平面AC ∴SA⊥DC,又AD⊥DC
∴DC⊥平面SAD ∴DC⊥AG
又由(1)有SC⊥平面AEF,AG 平面AEF
平面AEF
∴SC⊥AG ∴AG⊥平面SDC ∴AG⊥SD
298. 如图9-38,已知平面a ∥平面b ,A、C∈a ,B、D∈b ,E、F分别为AB、CD的中点.求证:EF∥a ,EF∥b .
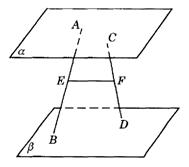
解析:当AB、CD共面时,平面ABCD∩a
=AC,平面ABCD∩b =BD.∵ a
∥b ,∴ AC∥BD.∵ E、F分别为AB、CD的中点,∴ EF∥AC.∵ AC
 a ,EF
a ,EF
 a ,∴ EF∥a
,同理EF∥b
.当AB、CD异面时,∵
a ,∴ EF∥a
,同理EF∥b
.当AB、CD异面时,∵ 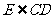 ,∴ 可在平面ECD内过点E作
,∴ 可在平面ECD内过点E作 ,与a ,b 分别交于
,与a ,b 分别交于 ,
, .平面
.平面 ,平面
,平面 ,∵ a ∥b ,∴
,∵ a ∥b ,∴  .∵ E是AB中点,∴ E也是
.∵ E是AB中点,∴ E也是 的中点.平面
的中点.平面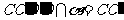 ,平面
,平面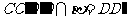 ,∵ a ∥b ,∴
,∵ a ∥b ,∴  ,∵ E、F分别为
,∵ E、F分别为 、CD中点,∴
、CD中点,∴ 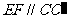 ,
,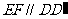 .∵
.∵ 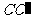
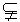 a ,EF
a ,EF
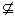 a ,∴ EF∥a
,同理EF∥b
.
a ,∴ EF∥a
,同理EF∥b
.
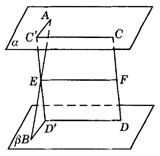
297. 如图9-37,两条异面直线AB、CD与三个平行平面a 、b 、g 分别相交于A、E、B,及C、F、D,又AD、BC与平面b 的交点为H、G.求证:EHFG为平行四边形.
 解析:
解析:
296.
如图9-35,平面a
∥平面b ,△ABC、△ 的分别在a 、b 内,线段
的分别在a 、b 内,线段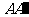 、
、 、
、 相交于点O,O在a 、b 之间.若AB=2,AC=1,∠ABC=60°,OA∶
相交于点O,O在a 、b 之间.若AB=2,AC=1,∠ABC=60°,OA∶ =3∶2,则△
=3∶2,则△ 的面积为________.
的面积为________.
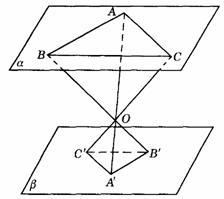
解析:图9-35
∵ 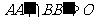 ,∴
,∴ 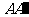 、
、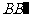 确定平面
确定平面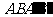 ,平面
,平面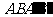 ∩a =AB,平面
∩a =AB,平面 ,∵ a ∥b ,∴
,∵ a ∥b ,∴ 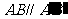 ,同理
,同理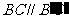 ,
,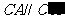 .由于方向相反,∴ △ABC与△
.由于方向相反,∴ △ABC与△ 的三内角相等,∴ △ABC∽△
的三内角相等,∴ △ABC∽△ .且
.且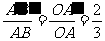 . ∵
. ∵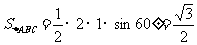 ,∴
,∴ 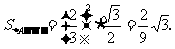
295. 已知空间不共面的四个点,与此四个点距离都相等的平面有________个.
解析:与不共面的四个点距离相等的平面分为两类,一类是四个点中一个点位于平面的一侧,另外三个点在平面的另一侧,这样的平面有4个;另一类是四个点中的两个点位于平面一侧,另外两个点在平面的另一侧,这样的平面有3个,故一共7个平面到这四个点距离相等.
294. 已知AC,BD是夹在两平行平面a 、b 间的线段,A∈a ,B∈a ,C∈b ,D∈b ,且AC=25cm,BD=30cm,AC、BD在平面b 内的射影的和为25cm,则AC、BD在平面b 内的射影长分别为________,AC与平面b 所成的角的正切值为________,BD与平面b 所成的角的正切值为________.
解析:设a 、b 间的距离为h,AC在平面b
内的射影 ,BD在平面b
内的射影
,BD在平面b
内的射影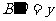 ,根据已知条件可得
,根据已知条件可得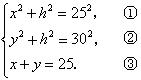 ②-①得
②-①得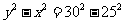 ,即
,即
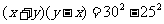 ,把③代入得y-x=11,∴
,把③代入得y-x=11,∴ 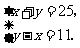 解得
解得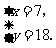 即
即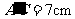 ,
,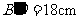 .又h=24cm,AC与平面b
所成的角为
.又h=24cm,AC与平面b
所成的角为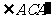 ,
,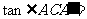
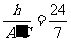 ,同理
,同理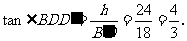
293. 平面a ∥平面b ,过平面a 、b 外一点P引直线PAB分别交a 、b 于A、B两点,PA=6,AB=2,引直线PCD分别交a 、b 于C、D两点.已知BD=12,则AC的长等于( ).
A.10 B.9 C.8 D.7
解析:B.如图答9-32,平面PBD∩a
=AC,平面PBD∩b =BD,∵ a
∥b ,∴ AC∥BD.由平面几何知识知,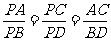 .∵ PA=6,AB=2,BD=12,∴
.∵ PA=6,AB=2,BD=12,∴ 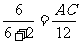 ,∴ AC=9.
,∴ AC=9.
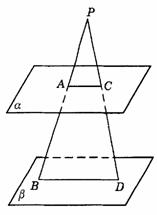
292. 设a 、b 是两个平面,l和m是两条直线,那么a ∥b 的一个充分条件是( ).
A.l a ,m
a ,m a ,且l∥b
,m∥b
B.l
a ,且l∥b
,m∥b
B.l a ,m
a ,m b ,且l∥m
b ,且l∥m
C.l⊥a ,m⊥b ,且l∥m D.l∥a ,m∥b ,且l∥m
解析:C.可参看图答9-31.
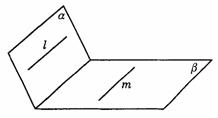
图答9-31
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com