
1. (10内江1)采集空气样品时,如果没有专业仪器,我们可用矿泉水瓶装满水到采样地点倒掉,这种收集气体的方法叫做________;实验室制氧气时,也可用这种方法收集,用该方法收集氧气时,制备氧气装置内空气配排尽的标志是________________。
排水法 导管口连续均匀冒出气泡
(10金华33)、某课外活动小组在学习了书本 “空气中氧气含量的测定”实验,知道P2O5 不能随便排放在空气中,否则会对空气造成污染,所以对该实验进行了改进:
在由两个注射器组成的密闭系统内共有50 mL空气,如右图。 然后给装有红磷的玻璃管加热。同时交替推动两个注射器的活塞,至玻璃管内的红磷变成白烟,且较长时间内无进一步变化时停止。停止加热后,待冷却至室温将气体全部推至一个注射器内。
然后给装有红磷的玻璃管加热。同时交替推动两个注射器的活塞,至玻璃管内的红磷变成白烟,且较长时间内无进一步变化时停止。停止加热后,待冷却至室温将气体全部推至一个注射器内。
请根据你对上述实验的理解,回答下列问题:
(1)实验结束后,注射器内的气体体积理论上应该减少约 mL。
(2)在实验的加热过程中,交替缓慢推动两个注射器的目的是 。写出该反应的化学方程式 。
(3)上述实验只是粗略测定空气中氧气含量的一种方法,你认为造成该实验不够精确的可能原因是 (写出其中一种) 。
(1) 10 mL。
(2) 是注射器内的氧气充分与红磷反应 。 4P+5O2==2P2O5 。(3)装置漏气等合理即可。
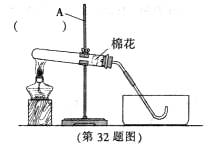 (10哈尔滨32)、(5分)实验室常用右图装置制取氧气,
(10哈尔滨32)、(5分)实验室常用右图装置制取氧气,
(1)在图中标出仪器A的名称,并将此制取氧气的装置图
补充完整
(2)写出用该装置制取氧气的化学方程式
答案:(1)画图要求:药品要平铺在试管底部;画出集气瓶且填充水槽和集气瓶内的水,液面画单实线,液体画虚线;导管口有气泡。(2)2KMnO4 K2MnO4+MnO2+O2↑
K2MnO4+MnO2+O2↑
9(10红河26)下图是常用的实验装置图,根据所学知识回答下列问题:
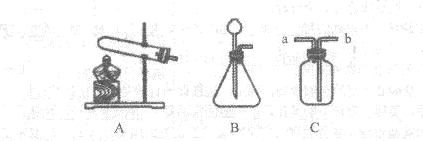
(1)若用A装置制取氧气,试管中盛放的药品是KclO3和MnO2(或KMnO4)(写名称也可),发生反应的化学方程式为 。
(2)通过查阅资料得知,硫化氢是一种有毒的气体,其密度比空气的大,且能溶于水形成氢硫酸。实验室通常用块状固体硫化亚铁(FeS)和稀硫酸混合,在常温下,通过发生反应制得硫化氢(H2S)气体。
制取硫化氢气体的发生装置可以选用 B (填编号),若用C装置收集硫化氢气体,气体应从 b 端通入(填“a”或“b”)。
2.(10茂名4)下列物质中不能在氧气里燃烧的是
A、氮气 B、木炭 C、红磷 D、铁
1. (10娄底15)氧气是一种化学性质比较活泼的气体,它可以和许多物质发生化学反应。如下图所示,关于这三个反应的叙述正确的是
(10娄底15)氧气是一种化学性质比较活泼的气体,它可以和许多物质发生化学反应。如下图所示,关于这三个反应的叙述正确的是
A.都放出热量
B.生成物都是固体
C.都产生蓝紫色火焰
D.都是非金属和氧气反应
1.(10娄底4)空气是一种宝贵的资源,空气中体积分数约占21%的是
A.二氧化碳 B.氮气 C.氧气 D.稀有气体
到附近的商店、工厂、学校作实际调查,了解函数在实际中的应用,把遇到的实际问题转化为建立函数关系、并作出解答,写出实习报告
以上,通过例题介绍了实习作业的基本要求和方法,并给出了实习报告的规范格式接下来,讨论一下,在我们的日常生活中,有哪些函数知识被实际所应用我们的实习活动以什么样的方式和方法来进行希望大家畅所欲言
四小结 :通过本节学习,明确了实习作业的基本要求和方法,以及实习报告的规范格式,用数学模型方法解决实际问题的一般步骤:提出问题、建立模型、分析求解、还原说明
例1 某城市现有人口总数为100万人,如果年自然增长率为1.2%,试解答下面的问题:
⑴写出该城市人口数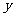 (万人)与年份
(万人)与年份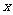 (年)的函数关系式;
(年)的函数关系式;
⑵计算10年以后该城市人口总数(精确到0.1万人);
⑶计算大约多少年以后该城市人口将达到120万人(精确到1年);
分析:此题是一道关于人口的典型问题,计划生育是我国的基本国策,通过此题可以让学生了解控制人口的现实意义
解:(1)1年后该城市人口总数为
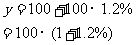
2年后该城市人口总数为:
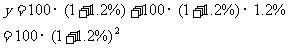
3年后该城市人口总数为:
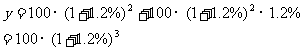
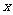 年后该城市人口总数为
年后该城市人口总数为
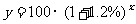 ;
;
(2)10年后该城市人口总数为:

⑶设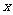 年后该城市人口将达到120万人,即
年后该城市人口将达到120万人,即
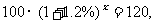
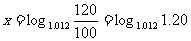
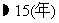
想一想:如果20年后该城市人口总数不超过120万人年自然增长率应该控制在多少?
设年自然增长率为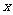 ,依题意有:
,依题意有:
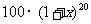 ≤120,
≤120,
由此有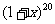 ≤120
≤120
由计算得: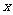 ≤0.9%
≤0.9%
即年自然增长率应控制在0.9%以内
此问题反映了控制人口的现实意义
实习报告的规范格式:
实习报告: 2003年10月9日
|
题目 |
某城市人口增长与人口控制 |
|
实际问题 |
某城市现有人口100万人,若年增长率为1.2%,试解答下面的问题: (1) 写出人口总数 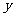 与年份 与年份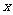 的函数式; 的函数式;(2) 计算10年以后该城市人口总数(精确到0.1万); (3) 大约多少年后人口达到120万人(精确到年); (4) 若20年后该城市人口总数不超过120万人,年增长率应该控制在多少? |
|
建立函数关系式 |
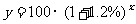 |
|
分析 与 解答 |
(1)
10年后人口总数为112.7万人; (2) 大约15年后人口达到120万人; |
|
说明 与 解释 |
若要20年后该城市人口总数不超过120万人,年自然增长率应控制在0.9%以内 |
|
负责人员及参加人员 |
|
|
指导教师审核意见 |
|
到附近的商店,工厂,学校实际调查,了解函数在实际中的应用,把遇到的问题转化为建立函数关系,并作出解答,写出实习报告
例2
|
题目 |
一定车流量情况下,十字路口红绿灯时间的确定 (黄灯时间忽略不计) |
|
实际问题 |
在xx附近十字路口经早、中、晚共15次对一周期(一个周期的时间长为90S),车流量的统计值分别是南北向15辆,东西向是30辆(每个方向只有一个车道);其它因素(如人流量和非机动车流量)忽略不计问如何确定十字路口红灯绿灯的时间(假定车流量分布均等)? |
|
建立函数 关系 |
要确定红绿灯时间,就是要使一个周期内,路口车辆等待的总时间最短,它由南北向和东西向车辆等待的总时间组成 |
|
分析与 解答 |
解:设在一个周期内,东西向绿灯,南北向红灯时间为t,则东西向红灯,南北向绿灯的时间为(90-t)S,一辆车等待最短时间为0,等待最长时间为t,设车流量是均匀的,则每一辆车平均等待时间为t/2;在一个周期内,南北向的车辆在路口等待的时间为 (15t/90)×(t/2)=(t2/12)(其中路口等待的车辆数为(15t/90)) 同理可得,东西方向的车辆在路口等待的总时间为 30×(90-t)÷90×(90-t)÷2=(90-t) ×(90-t)÷6 设一个周期内,路口车辆等待时间为y,则 y=t2/12+(90-t)2 /6=(60-t)2/4+450 ∴当t=60S的时候,y=450 ∴90-t=30S 答:东西向绿灯时间为60S,南北向绿灯时间为30S |
|
说明与 解释 |
这个模型的建立较理想化,这是由于知识的局限性 |
|
负责人及 参加人员 |
李冬(组长)、王凯、宋晓晨 |
|
指导教师 审核意见 |
选题不错,建议多十字路口调查,以准确掌握确定红绿灯时间的确定与车流量的关系 马试验 2003.10. |
例3
|
题目 |
当车站的客流量为多大时,需建立过轨天桥 |
|
实际问题 |
一些大中城市的火车站,客流量非常大,平均每十几分钟就会有一列客车进站或发车,为了减少车站压力,使旅客尽可能少的在车站逗留,当客流量超过一定量时,就会在站台设立过轨天桥当客流量超过多少时?在车站要设立过轨天桥 经调查知:在大中型车站设有8个检票通道口,平均每人检票需1.5秒;每节车厢平均会有30人下车,每列车有15节列车车厢,而且车站为了方便旅客,会让旅客提前10分钟进站,平均每次检票过程大约需要10分钟,旅客从下车走到检票口大约要3分钟.  |
|
建立函数关系 |
 |
|
分析与解答 |
 |
|
说明与 解释 |
1. 检票口为4个进站口,4个出站口,一般情况下不通用 2. 客流量包括进站人数和出站人数 3. 调查情况为平时情况,不包括节假日及春运期间 |
|
负责人及参加人员 |
李冬(组长)、王凯、宋晓晨 |
|
指导教师审核意见 |
选题很好,为车站科学决策提供了理论依据 马试验 2003.10. |
例4
|
题目 |
水利兴修问题 |
|
实际问题 |
兴修水利所开渠道断面为等腰梯形,腰与水平线的夹角为60°,要求湿透长度(即断面与水接触的边界长度)为定值L,问渠深多少时,可使流量最大 |
|
建立函数关系 |
渠深与流量都是可变的,在水的流速一定的条件下,水流量的大小是由断面面积大小来确定的,因此,本题实际上是求:渠深多少时,断面面积最大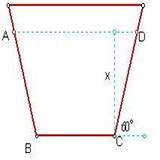 |
|
分析与解答 |
 |
|
说明与解释 |
(略) |
|
负责人及参加人员 |
李冬(组长)、王凯、宋晓晨 |
|
指导教师审核意见 |
选题很好,为农村水利建设科学决策提供了理论依据 马试验 2003.10. |
例5
|
题目 |
关于银行储蓄获利问题 |
|
实际问题 |
在当今社会有些人赚了钱,就存入银行,一则保险,二则获利,何乐而不为为了获取最多的利益,我们建议大家参考以下数据,三思而后行! |
|
建立函数关系 |
存法:都为三年,不满则转存,每次都存定金a元) (计算有错!) (计算有错!)注:不按复利、不按零存整取、整存零取、定活两便; |
|
分析与解答 |
分析:由以上五种数据可以看出;采用一次性存三年的,利息最低,而先存2年,再存1年的、转存6个月、3个月的,利息递增 答案:综上所述采用第一种方案即到(满)三个月就转存一次的获利最大 |
|
说明与解释 |
此答案并不确定,因人而异爱钱如命的,采用第一种方法普通人(正常人)采用2、3、4种方法家人较忙的采用最后一种方法 注:如果你的资金相当大,最好选1、2,因为那样所得的利息相当可观(腿累心欢!) |
|
负责人及参加人员 |
李冬(组长)、王凯、宋晓晨 |
|
指导教师审核意见 |
选题具有一般意义,对储蓄户有一定的参考作用 马试验 2003.10. |
本题该小组计算错误,教师有意不点破,让学生去发现和讨论正确结果恰恰相反,说明学生对一些实际生活问题并不了解
前面,我们一起学习了函数的应用举例,明确了函数知识在实际生产、生活中被广泛地应用在日常生活中,大家可以到附近的商店、工厂作实际调查,了解函数在实际中的应用,把遇到的实际问题转化为建立函数关系,并作出解答,写出实习报告
接下来,我们通过例题向大家说明实习作业的基本要求和方法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com