
14、(湖北省三校联合体高2008届2月测试)随着机构改革的深入进行,各单位要减员增效,有一家公司现有职员2a人(140<2a<420,且a为偶数 ,每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的
,每人每年可创利b万元. 据评估,在经营条件不变的前提下,每裁员1人,则留岗职员每人每年多创利0.01b万元,但公司需付下岗职员每人每年0.4b万元的生活费,并且该公司正常运转所需人数不得小于现有职员的 ,为获得最大的经济效益,该公司应裁员多少人?
,为获得最大的经济效益,该公司应裁员多少人?
解:设裁员x人,可获得的经济效益为y万元,则
 ……………4分
……………4分
依题意
 ……………6分
……………6分
(1)当 取到最大值;……………8分
取到最大值;……………8分
(2)当 取到最大值;……………10分
取到最大值;……………10分
答:当 ,
, ……………12分
……………12分
13、(湖北省八校高2008第二次联考)两家共同拥有一块土地 ,形状是等腰直角三角形,
,形状是等腰直角三角形, ,
, m,如果两家人准备划分一条分割线(直线段),使两家所得土地相等,其中
m,如果两家人准备划分一条分割线(直线段),使两家所得土地相等,其中 分别在线段
分别在线段 上.
上.
(Ⅰ)如果准备在分割线上建造一堵墙,请问如何划分割线,才能使造墙费用最少;
(Ⅱ)如果准备在分割线上栽种同一种果树,请问如何划分割线,才能使果树的产量最大.
解:设AQ=x,AP=y,  ,又
,又 ,
, .
.
PQ= .
.
(1) ,
,  ,此时
,此时 ,又
,又 .
.
即取AP=AQ= m时,PQ的长最短,因而造墙费用最少.
…………(6分)
m时,PQ的长最短,因而造墙费用最少.
…………(6分)
(2) ,
,
 .
.
考察函数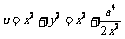 ,得当
,得当 时,函数递增,当
时,函数递增,当 时,函数递减, 所以函数的最大值
时,函数递减, 所以函数的最大值 ,此时
,此时 .
.
故当P取在B点,Q取在AC的中点处时,PQ最长,因而果树的产量最大. ……(12分)
12、(黑龙江省哈尔滨三中2008年高三上期末)某小型自来水厂的蓄水池中存有400吨水,水厂每小时可向蓄水池中注入自来水60吨,若蓄水池向居民不断的供水,且t小时内供水总量为210· 吨。
吨。
(1)供水开始几小时后,蓄水池中的水量为最小?最小水量为多少吨?
(2)若蓄水池中的水量小于200吨,就会出现供水紧张问题,试问在一天的24小时内,有多少小时会出现供水紧张情况?
答案:(1) 小时,400-140
小时,400-140 吨
吨
(2)10.5小时
11、为贯彻落实党的十七大精神,加快新农村建设步伐,红星镇政府投资c万元生产甲乙两种商品,据测算,投资甲商品x万元,可获得利润P=x万元,投资乙商品x万元可获得利润Q=40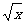 万元,如果镇政府聘请你当投资顾问,试问对甲乙两种商品的资金投入分别是多少万元?才能获得最大利润,获得最大利润是多少万元?
万元,如果镇政府聘请你当投资顾问,试问对甲乙两种商品的资金投入分别是多少万元?才能获得最大利润,获得最大利润是多少万元?
解:设对甲厂投入x万元(0≤x≤c),则对乙厂投入为c-x万元.所得利润为
y=x+40 (0≤x≤c) ……………………(3分)
(0≤x≤c) ……………………(3分)
令 =t(0≤t≤
=t(0≤t≤ ),则x=c-t2
),则x=c-t2
∴y=f(t)=-t2+40t+c=-(t-20)2+c+400……………………(6分)
当 ≥20,即c≥400时,则t=20, 即x=c-400时, ymax =c+400… (8分)
≥20,即c≥400时,则t=20, 即x=c-400时, ymax =c+400… (8分)
当0< <20,
即0<c<400时,则t=
<20,
即0<c<400时,则t= ,即x=0时,ymax=40
,即x=0时,ymax=40  .…(10分)
.…(10分)
答:若政府投资c不少于400万元时,应对甲投入c-400万元, 乙对投入400万元,可获得最大利润c+400万元.政府投资c小于400万元时,应对甲不投入,的把全部资金c都投入乙商品可获得最大利润40 万元.…(12分)
万元.…(12分)
10、设有关于x的不等式

(1)
(2)当a为何值时,此不等式的解集为R(本题满分12分)
解: 时,不等式可化为
时,不等式可化为 …………………………… 2分
…………………………… 2分
由 ……………………………………………..4分
……………………………………………..4分
 …………………………………………………………5分
…………………………………………………………5分

 …………………………………………………………….7分
…………………………………………………………….7分
欲使 恒成立,即
恒成立,即 恒成立,
恒成立,
只须 即可
即可
 ……………………………………………………….. 10分
……………………………………………………….. 10分
9、(河北衡水中学2008年第四次调考)已知函数 ,点
,点 是函数
是函数 图像上任意一点,点
图像上任意一点,点 关于原点的对称点
关于原点的对称点 的轨迹是函数
的轨迹是函数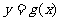 的图像
的图像
(1)当 时,解关于
时,解关于 的不等式
的不等式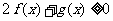 ;
;
(2)当 ,且
,且 时,总有
时,总有 恒成立,求
恒成立,求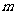 的取值范围.
的取值范围.
解:由题意知:P、Q关于原点对称,设Q(x,y)是函数y=g(x)图像上任一点,则P(-x,-y)是f(x)=loga(x+1)上的点,所以-y=loga(-x+1),于是g(x)=-loga(1-x).
(1)0<a<1,


(2) 时
时


设



8、(广东省深圳外国语学校2008届第三次质检)据调查,某地区100万从事传统农业的农民,人均收入3000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有x(x>0)万人进企业工作,那么剩下从事传统农业的农民的人均收入有望提高2x%,而进入企业工作的农民的人均收入为3000a元(a>0)。
(I)在建立加工企业后,要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入,试求x的取值范围;
(II)在(I)的条件下,当地政府应该如何引导农民(即x多大时),能使这100万农民的人均年收入达到最大。
解:(I)由题意得(100-x)·3000·(1+2x%)≥100×3000,
即x2-50x≤0,解得0≤x≤50, ……………………4分
又∵x>0 ∴0<x≤50; ……………………6分
(II)设这100万农民的人均年收入为y元,
则y= =
=-[x-25(a+1)]2+3000+475(a+1)2 (0<x≤50) ………………9分
(i)当0<25(a+1)≤50,即0<a≤1,当x=25(a+1)时,y最大; ………………11分
(ii)当25(a+1)>50,即a >1,函数y在(0,50]单调递增,∴当x=50时,y取最大值。…………13分
答:在0<a≤1时,安排25(a +1)万人进入企业工作,在a>1时安排50万人进入企业工作,才能使这100万人的人均年收入最大 ………………14分
7、 (广东省揭阳市2008年高中毕业班高考调研测试)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
(广东省揭阳市2008年高中毕业班高考调研测试)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求B在AM上,D在AN上,且对角线MN过C点,已知|AB|=3米,|AD|=2米,
(1) 要使矩形AMPN的面积大于32平方米,则AN的长应在什么范围内?
(2)
若|AN| 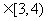 (单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
(单位:米),则当AM、AN的长度是多少时,矩形花坛AMPN的面积最大?并求出最大面积.
解:设AN的长为x米(x >2)
∵ ,∴|AM|=
,∴|AM|=
∴SAMPN=|AN|•|AM|= ------------------------------------- 4分
------------------------------------- 4分
(1)由SAMPN > 32 得
 > 32 ,
> 32 ,
∵x >2,∴ ,即(3x-8)(x-8)> 0
,即(3x-8)(x-8)> 0
∴ 即AN长的取值范围是
即AN长的取值范围是 ----------- 8分
----------- 8分
(2)令y= ,则y′=
,则y′= -------------- 10分
-------------- 10分
∵当 ,y′< 0,∴函数y=
,y′< 0,∴函数y= 在
在 上为单调递减函数,
上为单调递减函数,
∴当x=3时y= 取得最大值,即
取得最大值,即 (平方米)
(平方米)
此时|AN|=3米,|AM|= 米
米
6、(福建省厦门市2008学年高三质量检查)某化工集团在靠近某河流修建两个化工厂,流
 经第一化工厂的河流流量为500万立方米/天,在两
经第一化工厂的河流流量为500万立方米/天,在两
个化工厂之间还有一条流量为200万立方米/天的支
流并入大河(如图)。第一化工厂每天排放含有某种
有害物质的工业废水2万立方米;第二化工厂每天
排放这种工业废水1.4万立方米,从第一化工厂排出
的工业废水在流到第二化工厂之前,有20%可自然
净化。
环保要求:河流中工业废水的含量应不大于0.2%,
因此,这两个工厂都需各自处理部分的工业废水,第
一化工厂处理工业废水的成本是1000元/万立方米,
第二化工厂处理工业废水的成本是800元/万立方米。
试问:在满足环保要求的条件下,两个化工厂应各自
处理多少工业废水,才能使这两个工厂总的工业废水
处理费用最小?
解:设第一化工厂每天处理工业废水x万立方米,
需满足: …………2分
…………2分
设第二化工厂每天处理工业废水y万立方米,
需满足: …………4分
…………4分
两个化工厂每天处理工业废水总的费用为1000x+800y元。
 问题即为:在约束条件
问题即为:在约束条件

求目标函数 的最小值。
的最小值。
5、(山东省博兴二中高三第三次月考)为了立一块广告牌,要制造一个三角形的支架. 三角形支架形状如图,要求 ,BC的长度大于1米,且AC比AB长0.5米.
为了广告牌稳固,要求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
,BC的长度大于1米,且AC比AB长0.5米.
为了广告牌稳固,要求AC的长度越短越好,求AC最短为多少米?且当AC最短时,BC长度为多少米?
解:如图,设BC的长度为x米,AC的长度为y米,则AB的长度
为(y-0.5)米. 在△ABC中,依余弦定理得:
 -------(4分)
-------(4分)
即
化简,得
∵ ,∴
,∴ 因此
因此 ------------------(6分)
------------------(6分)
方法一: .
-------------------- (10分)
.
-------------------- (10分)
当且仅当 时,取“=”号,即
时,取“=”号,即 时,y有最小值
时,y有最小值 .
.
方法二: -----------------(9分)
-----------------(9分)
解 ,得
,得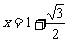 ------------------------(11分)
------------------------(11分)
∵当 时,
时, ;当
;当 时,
时,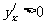 .
.
∴当 时,y有最小值
时,y有最小值 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com