
1. 下列各句中,没有错别字的一项是
A.书刊要装帧,门面要装潢,居室要装修,营造一个舒适温馨而又口味高雅的家可以说是工薪阶层中许多人的梦想。
B.舞台上,弟弟的朗颂声情并茂,姐姐的伴奏锦上添花;母亲心中的那丝担忧很快便烟消云散了。
C.2008 年 1 月以来,中国居民物价指数 CPI 出现了明显的涨幅,不少低收入家庭倍感通货膨涨的压力。
D.在骄阳的曝晒下,牵牛花堰旗息鼓,美人蕉慵倦无力,矜持的牡丹也耷拉下了高贵的头颅,失去了先前的神采。
[答案] A
[解析]B 颂-诵; C 涨-胀;D 堰-偃。
例文1
黑龙江 考生
欢迎你们来到这里,与我院共同探讨有关记忆移植的科研成果,下面我就来简述一下我院对此课题的认识与看法。移植记忆的原理在于:进入大脑的信息经过编码贮存在一种化学物质里,转移这种化学物质,记忆便可随之转移。我院已经成功地将羊的记忆移植成功,对于试验体的发展状况处在一步的观察之中。
我想诸位更关心的问题是人的记忆可否移植,我院的研究结论是肯定的。
首先,虽然人脑的记忆细胞多而复杂,但经电脑分析,它具有很规律的DNA排列结构。
其次,我们要根据这种规律性结构利用电脑仿制一个细胞体。
最后,将这个细胞体植入另一个实验体中。记忆移植结束。
各位一定相当关心这种移植方法的成功率。经过我院的反复试验,这种方法在哺
乳类动物中的成功率是75%记忆的移植对于未来的世界是有着巨大的影响和深远的意义的。
信息时代生产力的高速发展依靠电脑和人脑的浅层记忆是不够的,如果我们将同一问题移植到不同的人脑中,就会得出几千种甚至上万种方案或结论。而记忆的移植可以缩短人类在记忆上所浪费的时间,这就间接地延长了人类的生命。
21世纪将是生物科学的世纪,记忆的移植方法无疑也是生物领域的重大突破,它会给21世纪的生物科学注入新的活力。
记忆移植的应用技术如果得以推广,会极大地促进生产力的发展,增强综合国力,使一些院士的研究课题得以延续到新人脑中继续开发和研究,对于科学领域来说也是一项巨大的贡献。
但我们同时也应看到:记忆移植的技术还并不发达,将无数人脑细胞作为实验体,能否得到科学界的认可还是一个问题,所以,我们应该找到更恰当的方法研究此课题,同时,也希望各位同行能够贡献自己的力量。谢谢各位!
简评:采用演讲稿的形式谈对记忆移植的看法,的确别具新意。文章思路清晰,视野开阔。先讲移植原理,再谈移植成果,主要笔墨放在“记忆在移植对于未来的世界是有着巨大的影响和深远的意义的”,最后,辨证分析,提出希望,全文语言简洁明快,朴实自然。
310. 平面α内有一个半圆,直径为AB,过A作SA⊥平面α,在半圆上任取一点M,连SM、SB,且N、H分别是A在SM、SB上的射影.(1)求证:NH⊥SB.(2)这个图形中有多少个线面垂直关系?(3)这个图形中有多少个直角三角形?(4)这个图形中有多少对相互垂直的直线?
解析:此题主要考查直线与直线,直线与平面的垂直关系及论证,空间想象力.
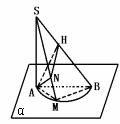
解 (1)连AM,BM.∵AB为已知圆的直径,如图所示.
∴AM⊥BM,
∵SA⊥平面α,MB α,
α,
∴SA⊥MB.
∵AM∩SA=A,∴BM⊥平面SAM.
∵AN 平面SAM,
平面SAM,
∴BM⊥AN.
∵AN⊥SM于N,BM∩SM=M,
∴AN⊥平面SMB.
∵AH⊥SB于H,且NH是AH在平面SMB的射影
∴NH⊥SB.
(2)由(1)知,SA⊥平面AMB,BM⊥平面SAM.AN⊥平面SMB.
∵SB⊥AH且SB⊥HN.
∴SB⊥平面ANH.
∴图中共有4个线面垂直关系
(3)∵SA⊥平面AMB,
∴ΔSAB、ΔSAM均为直角三角形.
∵BM⊥平面SAM,∴ΔBMA,ΔBMS均为直角三角形.
∵AN⊥平面SMB.∴ΔANS、ΔANM、ΔANH均为直角三角形.
∵SB⊥平面AHN. ∴ΔSHA、ΔBHA、ΔSHN均为直角三角形
综上所述,图中共有10个直角三角形.
(4)由SA⊥平面AMB知:SA⊥AM,SA⊥AB,SA⊥BM;
由BM⊥平面SAM知:BM⊥AM,BM⊥SM,BM⊥AN;
由AN⊥平面SMB知:AN⊥SM,AN⊥SB,AN⊥NH;
SB⊥平面AHN知:SB⊥AH,SB⊥HN;
综上所述,图中有11对互相垂直的直线.
309. 在空间四边形ABCP中,PA⊥PC,PB⊥BC,AC⊥BC.PA、PB与平面ABC所成角分别为30°和45°。(1)直线PC与AB能否垂直?证明你的结论;(2)若点P到平面ABC的距离为h,求点P到直线AB的距离.
解析:主要考查直线与直线、直线与平面的位置关系的综合应用及线面角,点面间距离等概念应用,空间想象力及推理能力.
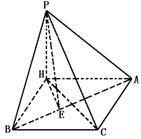
解 (1)AB与PC不能垂直,证明如下:假设PC⊥AB,作PH⊥平面ABC于H,则HC是PC在平面ABC的射影,∴HC⊥AB,∵PA、PB在平面ABC的射影分别为HB、HA,PB⊥BC,PA⊥PC.
∴BH⊥BC,AH⊥AC
∵AC⊥BC,∴平行四边形ACBH为矩形.
∵HC⊥AB,∴ACBH为正方形.
∴HB=HA
∵PH⊥平面ACBH.∴ΔPHB≌ΔPHA.
∴∠PBH=∠PAH,且PB,PA与平面ABC所成角分别为∠PBH,∠PAH.由已知∠PBH=45°,∠PAH=30°,与∠PBH=∠PAH矛盾.
∴PC不垂直于AB.
(2)由已知有PH=h,∴∠PBH=45°
∴BH=PH=h.∵∠PAH=30°,∴HA=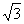 h.
h.
∴矩形ACBH中,AB=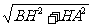 =
=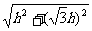 =2h.
=2h.
作HE⊥AB于E,∴HE=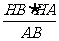 =
=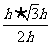 =
=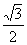 h.
h.
∵PH⊥平面ACBH,HE⊥AB,
由三垂线定理有PE⊥AB,∴PE是点P到AB的距离.
在RtΔPHE中,PE=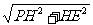 =
=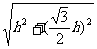 =
=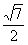 h.
h.
即点P到AB距离为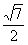 h.
h.
评析:此题属开放型命题,处理此类问题的方法是先假设结论成立,然后“执果索因”,作推理分析,导出矛盾的就否定结论(反证法),导不出矛盾的,就说明与条件相容,可采用演绎法进行推理,此题(1)属于反证法.
308. 空间四边形PABC中,PA、PB、PC两两相互垂直,∠PBA=45°,∠PBC=60°,M为AB的中点.(1)求BC与平面PAB所成的角;(2)求证:AB⊥平面PMC.
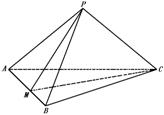
解析:此题数据特殊,先考虑数据关系及计算、发现解题思路.
解 ∵ PA⊥AB,∴∠APB=90°
在RtΔAPB中,∵∠ABP=45°,设PA=a,
则PB=a,AB=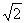 a,∵PB⊥PC,在RtΔPBC中,
a,∵PB⊥PC,在RtΔPBC中,
∵∠PBC=60°,PB=a.∴BC=2a,PC=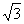 a.
a.
∵AP⊥PC ∴在RtΔAPC中,AC=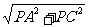 =
=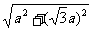 =2a
=2a
(1)∵PC⊥PA,PC⊥PB,∴PC⊥平面PAB,
∴BC在平面PBC上的射影是BP.
∠CBP是CB与平面PAB所成的角
∵∠PBC=60°,∴BC与平面PBA的角为60°.
(2)由上知,PA=PB=a,AC=BC=2a.
∴M为AB的中点,则AB⊥PM,AB⊥CM.
∴AB⊥平面PCM.
说明 要清楚线面的垂直关系,线面角的定义,通过数据特点,发现解题捷径.
307. 矩形ABCD,AB=2,AD=3,沿BD把ΔBCD折起,使C点在平面ABD上的射影恰好落在AD上.
(1)求证:CD⊥AB;
(2)求CD与平面ABD所成角的余弦值.
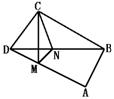
(1)证明 如图所示,∵CM⊥面ABD,AD⊥AB,
∴CD⊥AB
(2)解:∵CM⊥面ABD
∴∠CDM为CD与平面ABD所成的角,
cos∠CDM=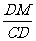
作CN⊥BD于N,连接MN,则MN⊥BD.在折叠前的矩形ABCD图上可得
DM∶CD=CD∶CA=AB∶AD=2∶3.
∴CD与平面ABD所成角的余弦值为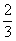
306. 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=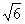 ,M是CC1的中点,求证:AB1⊥A1M.
,M是CC1的中点,求证:AB1⊥A1M.
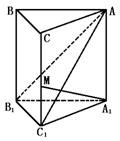
解析:不难看出B1C1⊥平面AA1C1C,AC1是AB1在平面AA1C1C上的射影.欲证A1M⊥AB1,只要能证A1M⊥AC1就可以了.
证:连AC1,在直角ΔABC中,BC=1,∠BAC=30°,
∴
AC=A1C1=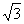 .
.
设∠AC1A1=α,∠MA1C1=β
∴
tanα=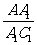 =
=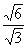 =
=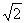 ,
,
tgβ=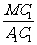 =
=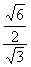 =
= .
.
∵cot(α+β)=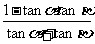 =
=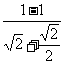 =0,
=0,
∴α+β=90° 即AC1⊥A1M.
∵B1C1⊥C1A1,CC1⊥B1C1,∴B1C1⊥平面AA1CC1,
AC1是AB1在平面AA1C1C上的射影.
∵AC1⊥A1M,∴由三垂线定理得A1M⊥AB1.
评注:本题在证AC1⊥A1M时,主要是利用三角函数,证α+β=90°,与常见的其他题目不太相同.
305. 求证:端点分别在两条异面直线a和b上的动线段AB的中点共面.
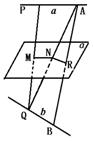
证明 如图,设异面直线a、b的公垂线段是PQ,PQ的中点是M,过M作平面α,使PQ⊥平面α,且和AB交于R,连结AQ,交平面α于N.连结MN、NR.∵PQ⊥平面α,MN α,∴PQ⊥MN.在平面APQ内,PQ⊥a,PQ⊥MN,∴MN∥a,a∥α,又∵PM=MQ,∴AN=NQ,同理可证NR∥b,RA=RB.
α,∴PQ⊥MN.在平面APQ内,PQ⊥a,PQ⊥MN,∴MN∥a,a∥α,又∵PM=MQ,∴AN=NQ,同理可证NR∥b,RA=RB.
即动线段的中点在经过中垂线段中点且和中垂线垂直的平面内.
304. ΔABC在平面α内的射影是ΔA′B′C′,它们的面积分别是S、S′,若ΔABC所在平面与平面α所成二面角的大小为θ(0<θ<90°=,则S′=S·cosθ.
证法一 如图(1),当BC在平面α内,过A′作A′D⊥BC,垂足为D.
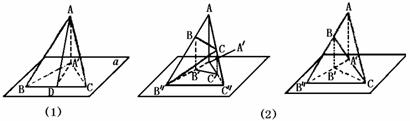
∵AA′⊥平面α,AD在平面α内的射影A′D垂直BC.
∴AD⊥BC.∴∠ADA′=θ.
又S′=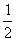 A′D·BC,S=
A′D·BC,S=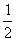 AD·BC,cosθ=
AD·BC,cosθ=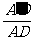 ,∴S′=S·cosθ.
,∴S′=S·cosθ.
证法二 如图(2),当B、C两点均不在平面α内或只有一点(如C)在平面α内,可运用(1)的结论证明S′=S·cosθ.
303. 平面α外一点A在平面α内的射影是A′,BC在平面内,∠ABA′=θ,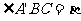 ,∠ABC=
,∠ABC= ,求证:cosγ=cosθ·cosβ.
,求证:cosγ=cosθ·cosβ.
解析: 过A′作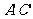 ⊥BC于C′,连AC′.
⊥BC于C′,连AC′.
∵AA′⊥平面α,BC垂直AC在平面α内的射线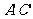 .
.
∴BC′⊥AC′,cos =
=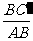 .
.
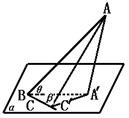
又∵cosθ=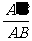 ,cosβ=
,cosβ=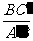 ,
,
∴cos =cosθ·cosβ.
=cosθ·cosβ.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com