
1.(2010年全国理14)正视图为一个三角形的几何体可以是______(写出三种)
[解析]三棱锥、三棱柱、圆锥等.
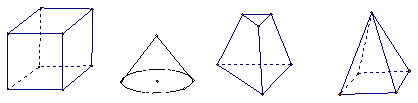
11.(2007年山东理3)下列几何体各自的三视图中,有且仅有两个视图相同的是
(A)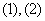 (B)
(B) 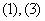 (C)
(C)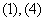 (D)
(D) 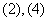
[答案]:D[分析]:从选项看只要判断正方体的三视图都相同就可以选出正确答案。
10.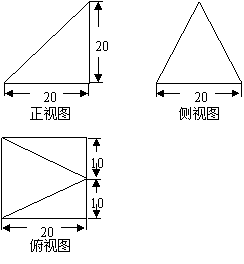 (2007年海南理8)已知某个几何体的三视图如下,根据图中标出 的尺寸(单位:cm),可得这个几何体的体积是( )
(2007年海南理8)已知某个几何体的三视图如下,根据图中标出 的尺寸(单位:cm),可得这个几何体的体积是( )
A.
B.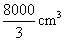
C.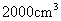
D.
[答案]:B[分析]:如图,
9.(2008年广东理5)将正三棱柱截去三个角(如图1所示 分别是
分别是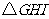 三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
三边的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )


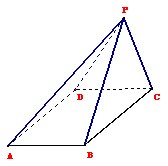 [解析]解题时在图2的右边放扇墙(心中有墙),可得答案A.
[解析]解题时在图2的右边放扇墙(心中有墙),可得答案A.
8.(2008年山东理6)右图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是( )
A.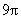 B.
B.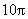 C.
C.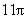 D.
D.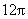
解:从三视图可以看出该几何体是由一个球和一个圆柱组合而成的,其表面及为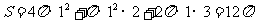
7.(2008年海南理12)某几何体的一条棱长为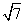 ,在该几何体的正视图中,这条棱的投影是长为
,在该几何体的正视图中,这条棱的投影是长为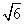 的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
的线段,在该几何体的侧视图与俯视图中,这条棱的投影分别是长为a和b的线段,则a+b的最大值为( )
 A.
A.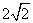 B.
B.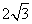 C.
C.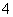 D.
D.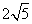
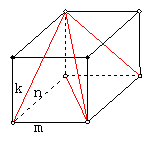
C解:结合长方体的对角线在三个面的投影来理解计算。如图
设长方体的高宽高分别为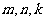 ,由题意得
,由题意得
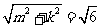
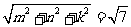 ,
,
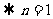
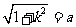 ,
,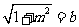 ,所以
,所以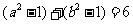
 ,
,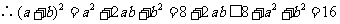
 当且仅当
当且仅当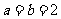 时取等号。
时取等号。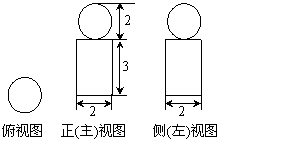
6.(2009年山东理4) 一空间几何体的三视图如图所示,则该几何体的体积为( ).
 A.
A.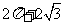 B.
B. 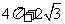 C.
C.
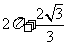 D.
D.
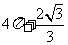
[解析]:该空间几何体为一圆柱和一四棱锥组成的,
圆柱的底面半径为1,高为2,体积为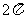 ,四棱锥的底面
,四棱锥的底面
边长为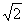 ,高为
,高为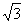 ,所以体积为
,所以体积为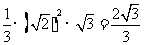
 所以该几何体的体积为
所以该几何体的体积为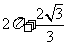 .
.
答案:C
[命题立意]:本题考查了立体几何中的空间想象能力,
由三视图能够想象得到空间的立体图,并能准确地
计算出.几何体的体积.
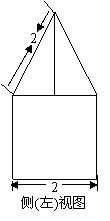
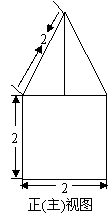
5.(2009年海南理11)一个棱锥的三视图如图,则该棱锥的全面积(单位:c )为
)为
(A)48+12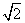 (B)48+24
(B)48+24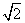
(C)36+12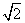 (D)36+24
(D)36+24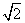
[解析]棱锥的直观图如右,则有PO=4,OD=3,由勾股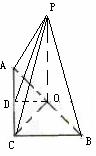 定理,得PD=5,AB=6
定理,得PD=5,AB=6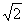 ,全面积为:
,全面积为: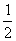 ×6×6+2×
×6×6+2×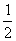 ×6×5+
×6×5+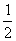 ×6
×6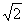 ×4=48+12
×4=48+12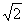 ,故选
,故选
4.(2010年北京理3)一个长方体去掉一个小长方体,所得几何体的正(主)视图与侧(左)视图分别如右图所示,则该几何体的俯视图为
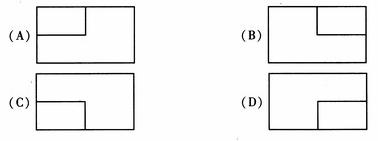
 解析:很容易看出这是一个面向我们的左上角缺了一小块长方体的图形,不难选出答案C。
解析:很容易看出这是一个面向我们的左上角缺了一小块长方体的图形,不难选出答案C。
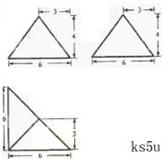
3.( 2010年安徽理8)一个几何体的三视图如图,该几何体的表面积为
A、280 B、292 C、360 D、372
[解析]该几何体由两个长方体组合而成,其表面积等于下面长方体的全面积加上面长方体的4个侧面积之 和。
和。 .
.
[方法技巧]把三视图转化为直观图是解决问题的关键.又三视图很容易知道是两个长方体的组合体,画出直观图,得出各个 棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
棱的长度.把几何体的表面积转化为下面长方体的全面积加上面长方体的4个侧面积之和。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com