
12.(2010浙江卷) 下列热化学方程式或离子方程式中,正确的是:
A.甲烷的标准燃烧热为-890.3kJ·mol-1,则甲烷燃烧的热化学方程式可表示为:
CH4(g)+2O2(g)=CO2(g)+2H2O(g) △H=-890.3kJ·mol-1
B. 500℃、30MPa下,将0.5mol N2和1.5molH2置于密闭的容器中充分反应生成NH3(g),放热19.3kJ,其热化学方程式为:
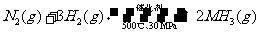 △H=-38.6kJ·
△H=-38.6kJ· mol-1
mol-1
C. 氯化镁溶液与氨水反应:
D. 氧化铝溶于NaOH溶液:
试题解析:
本题考查热化学方程式与离子方程式的书写。A、标准燃烧热的定义,1mol可燃物完全燃烧生成稳定氧化物时方出的热量(标准指298K,1atm)。水液态稳定,方程式系数就是物质的量,故A错。B、根据热化学方程式的含义,与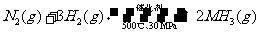 对应的热量是1mol氮气完全反应时的热量,但次反应为可逆反应故,投入0.5mol的氮气,最终参加反应的氮气一定小于0.5mol。所以△H的值大于38.6。B错。D、氢氧化铝沉淀没有沉淀符号。
对应的热量是1mol氮气完全反应时的热量,但次反应为可逆反应故,投入0.5mol的氮气,最终参加反应的氮气一定小于0.5mol。所以△H的值大于38.6。B错。D、氢氧化铝沉淀没有沉淀符号。
本题答案:C
教与学提示:
化学用语的教学是化学学科技术规范,强调准确性,强调正确理解与应用。特别重视热化学方程式的系数与反应热的对应关系。重视离子方程式的拆与不拆的问题。热化学方程式的书写问题由:聚集状态、系数、系数与反应热数值对应、反应热单位、可逆反应的反应热等内容构成。离子方程式的书写问题由:强弱电解质、最简整数比、定组成规律、离子方程式正误判断、守恒、定量离子方程式等内容组成。
9.(2010广东理综卷)
在298K、100kPa时,已知:2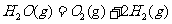 ⊿
⊿
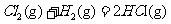 ⊿
⊿
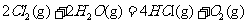 ⊿
⊿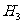
则⊿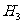 与⊿
与⊿ 和⊿
和⊿ 间的关系正确的是
间的关系正确的是
A .⊿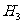 =⊿
=⊿ +2⊿
+2⊿ B ⊿
B ⊿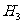 =⊿
=⊿ +⊿
+⊿
C. ⊿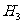 =⊿
=⊿ -2⊿
-2⊿ D. ⊿
D. ⊿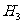 =⊿
=⊿ - ⊿
- ⊿
解析:第三个方程式可由第二个方程式乘以2与第一个方程式相加,有盖斯定律可知
答案:A
6.(2010天津卷)下列各表述与示意图一致的是

A.图①表示25℃时,用0.1 mol·L-1盐酸滴定20 mL 0.1 mol·L-1 NaOH溶液,溶液的pH随加入酸体积的变化
B.图②中曲线表示反应2SO2(g) + O2(g)  2SO3(g);ΔH < 0 正、逆反应的平衡常数K随温度的变化
2SO3(g);ΔH < 0 正、逆反应的平衡常数K随温度的变化
C.图③表示10 mL 0.01 mol·L-1 KMnO4 酸性溶液与过量的0.1 mol·L-1 H2C2O4溶液混合时,n(Mn2+) 随时间的变化
D.图④中a、b曲线分别表示反应CH2=CH2 (g) + H2(g) CH3CH3(g);ΔH< 0使用和未使用催化剂时,反应过程中的能量变化
CH3CH3(g);ΔH< 0使用和未使用催化剂时,反应过程中的能量变化
解析:酸碱中和在接近终点时,pH会发生突变,曲线的斜率会很大,故A错;正逆反应的平衡常数互为倒数关系,故B正确;反应是放热反应,且反应生成的Mn2+对该反应有催化作用,故反应速率越来越快,C错;反应是放热反应,但图像描述是吸热反应,故D错。
答案:B
命题立意:综合考查了有关图像问题,有酸碱中和滴定图像、正逆反应的平衡常数图像,反应速率图像和能量变化图像。
12. 答案D
[解析]本题考查盖斯定律的计算。由已知得:Br2(l)=Br2(g) H=+30KJ/mol,则H2(g) + Br2(g) = 2HBr(g);H= -102KJ/mol。436+a-2×369=-102;a=―200KJ,D项正确。
12.(2010重庆卷)已知 蒸发1mol Br2(l)需要吸收的能量为30kJ,其它相关数据如下表:
蒸发1mol Br2(l)需要吸收的能量为30kJ,其它相关数据如下表:

则表中a为
A.404 B.260 C.230 D.200
22.本题主要考查函数、导数、不等式的证明等基础知识,同时考查综合运用数学知识进行推理论证的能力和分类讨论的思想.(满分14分)
解:(I)
(II)由(I)知,
令
则
(i)当
若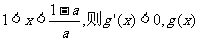 是减函数,所以
是减函数,所以
即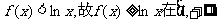 上不恒成立.
上不恒成立.
(ii)当
若 是增函数,所以
是增函数,所以
即 时,
时,
综上所述,所求a的取值范围为

整理得

解法二:用数学归纳法证明.
(1)当n=1时,左边=1,右边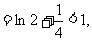 不等式成立.
不等式成立.
(2)假设n=k时,不等式成立,就是

那么
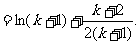

22. (本小题满分14分)
已知函数f(x)=ax+ +c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
+c(a>0)的图象在点(1,f(1))处的切线方程为y=x-1.
(Ⅰ)用a表示出b,c;
(Ⅱ)若f(x)>㏑x在[1,∞]上恒成立,求a的取值范围;
(Ⅲ)证明:1+ +
+ +…+
+…+ >㏑(n+1)+
>㏑(n+1)+ )(n≥1).
)(n≥1).
21、(本小题满分12分)
已知函数 .
.
(Ⅰ)讨论函数 的单调性;
的单调性;
(Ⅱ)设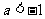 .如果对任意
.如果对任意 ,
, ,求
,求 的取值范围.
的取值范围.

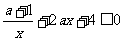 .
.
从而 .
.
故 的取值范围为
的取值范围为 . …………12分
. …………12分
20、解:(1)由 得
得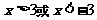 又
又
由 知
知
(2)函数 在
在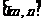 上单调递增,又
上单调递增,又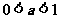 故
故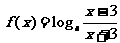 在
在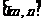 上单调递减,得
上单调递减,得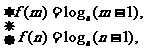
即 是方程
是方程 的两个实根,
的两个实根,
原问题等价于方程 在
在 上有两个不等的实根。
上有两个不等的实根。
由 得
得 ,
,
记: 则应有:
则应有:


故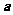 的取值范围是
的取值范围是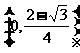 。
。
20、本小题满分12分)设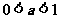 ,函数
,函数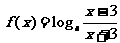 的定义域为
的定义域为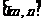 ,值域为
,值域为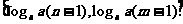 。
。
(1)求证: ;
;
(2)求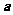 的取值范围。
的取值范围。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com