2．课时划分

《函数y＝Asin(ωx+φ)的图象》的教学分两个课时完成：

第一课时：函数y＝sinx到y＝Asin(ωx+φ) 的图象变换规律的探索;

第二课时：函数y＝Asin(ωx+φ) 的图象的作法及应用；

1．教材的地位和作用

本节课内容是人教A版数学必修4第一章第五节《函数y＝Asin(ωx+φ)的图象》，是在学生已经学习了正、余弦函数的图象和性质的基础上，进一步研究生活生产实际中常见的函数类型：函数y＝Asin(ωx+φ)的图象.在解决这个问题的过程中贯穿了由简单到复杂、特殊到一般的化归数学思想.同时还力图向学生展示观察、归纳、类比、联想等数学思想方法，通过本节内容的学习可以使学生将已有的知识形成体系，对于进一步探索、研究其他数学问题有很强的启发与示范作用.

4. 让学生在与同伴的合作探讨过程中，学会运用数学语言进行交流，学会辨证地看问题，学会倾听、学会发现同伴的优点，学会进行信息整合，能从同伴的发言中提出自己的观点．

3. 培养学生的“问题意识”，在探索中学会将“知识问题化”，大胆、合理地提出猜测，通过证明、完善，最终达到将“问题知识化”的目的．

2. 激发学生的探究欲望，通过对函数y＝sinx到y＝Asin(ωx+φ)的图象变换规律的探索，能够自我总结形成解决问题的一般方法．体会由简单到复杂，特殊到一般的化归思想。

1. 让学生在掌握函数y=Asin(wx+j)的图象探究方法的基础上，正确找出由函数y＝sinx到y＝Asin(ωx+φ) 的图象变换规律，会用“图像变换” 画出y＝Asin(ωx+φ) 的图象。

5．注重学生个性发展．

对课本例1进行分解与降低，进一步体会参数φ、ω、Α对函数图像的形状和位置的影响；例2的设计是上述三个过程的合成，这样安排既分散了难点，又使学生形成清晰的线索，从中能使学生学习如何将复杂的问题分解为简单的问题并“各个击破”，然后“归纳整合”，培养有条理地思考的习惯，有利于培养学生的逻辑思维能力。练习设计则降低对知识的要求，使得不同层次的学生都能得到相应的训练，提高课堂的思维效率；思考题的设计有利于延伸“图像变换”的方法，让学生寻找不同的变换途径，拓展思维；作业中的选做题为学有余力的学生提供进一步发展的空间。

4. 计算机作图，动态演示，应用灵活．

现代信息技术在数学的教学过程中运用越来越广泛，能够利用计算机进行一些简单的数学实验也将成为将来数学教学的一个发展趋势。在本节授课过程中，共设计使用了多次计算机演示操作，练习中使用几何画板，将授课过程中的难点一一化解.尤其是在参数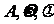对函数图象的影响探究过程中，画板的使用使本来非常难处理的问题简单化、直观化，给学生提供一种验证猜想合理性的途径。

3. 充分尊重学生的思维活动和合作探究。

在分组合作探究的过程中给学生想的时间、说的机会以及展示思维过程的舞台；在活动中引导学生用归纳的思维方法思考问题。

2.从“知识问题化”到 “问题知识化”

心理学家布鲁纳指出：“教学过程是一种提出问题和解决问题的持续不断的活动。”在新的教学理念下，教师要善于把问题抛给学生，思维永远是从问题开始的，因此，本节课采用了逐步设疑、诱导、解疑，指导学生去发现的方法，使学生始终处于兴奋的状态之中。培养学生的“问题意识”，在探索中学会将“知识问题化”，大胆、合理地提出猜测，通过证明、完善，最终达到将“问题知识化”的目的。