
3.通过习题与探究知识的相关性设置,引导学生深入探究得出判断函数的零点个数和所在区间的方法;
2.通过数形结合思想的渗透,培养学生主动应用数学思想的意识;
1.通过化归与转化思想的引导,培养学生从已有认知结构出发,寻求解决棘手问题方法的习惯;
3.结合几类基本初等函数的图象特征,掌握判断函数的零点个数和所在区间的方法.
本节课是学生在学习了函数的性质,具备了初步的数形结合知识的基础上,通过对特殊函数图象的分析进行展开的,是培养学生“化归与转化思想”,“ 数形结合思想”, “函数与方程思想”的优质载体。
结合本节课教学主线的设计,设定本节课的过程与方法目标如下:
2.结合零点定义的探究,掌握方程的实根与其相应函数零点之间的等价关系;
结合本节课引入三大知识点的方法,设定本节课的知识与技能目标如下:
1.结合方程根的几何意义,理解函数零点的定义;
本节内容包含三大知识点:
普通高中课标教材必修1共安排了三章内容,第一章是《集合与函数的概念》,第二章是《基本初等函数(Ⅰ)》,第三章是《函数的应用》。第三章编排了两块内容,第一部分是函数与方程,第二部分是函数模型及其应用。本节课方程的根与函数的零点,正是在这种建立和运用函数模型的大背景下展开的。本节课的主要教学内容是函数零点的定义和函数零点存在的判定依据,这两者显然是为下节“用二分法求方程近似解”这一“函数的应用”服务的,同时也为后续学习的算法埋下伏笔。由此可见,它起着承上启下的作用,与整章、整册综合成一个整体,学好本节意义重大。
函数在数学中占据着不可替代的核心地位,根本原因之一在于函数与其他知识具有广泛的联系,而函数的零点就是其中的一个链结点,它从不同的角度,将数与形,函数与方程有机地联系在一起。方程本身就是函数的一部分,用函数的观点来研究方程,就是将局部放入整体中研究,进而对整体和局部都有一个更深层次的理解,并学会用联系的观点解决问题,为后面函数与不等式和数列等其他知识的联系奠定基础。
3. 培养学生勇于创新而又不失严谨的思维习惯和在探索真理时锲而不舍的钻研精神.
重点与难点:
本节课的教学重点是归纳推理的概念理解和应用;教学难点是提高学生从特殊到一般的归纳能力.
教学方式:
本节课采用的是启发式教学,综合使用了讲授、问答、活动等多种教学方式.
教学工具:
多媒体、圆纸片、硬币.
教学过程:
|
教学设计 |
设计意图 |
|
一. 问题引入,激发兴趣 华罗庚爷爷讲的小故事: 有位老师想辨别他的两个学生谁更聪明. 他采用如下的方法:事先准备好两顶白帽子,一顶黑帽子,让学生们看到,然后让他们闭上眼睛. 老师给他们戴上帽子,并把剩下的那顶帽子藏起来. 最后让学生睁开眼睛,看着对方的帽子,说出自己所戴帽子的颜色. 两个学生互相望了望,犹豫了一小会儿,然后异口同声地说:“我们戴的是白帽子” . 聪明的各位,想想看,他们是怎么知道的? 学生发言,教师点评. 这里的思维方式就是推理. |
通过华先生的经典问题,启发学生思考,激发学生兴趣.(华先生的原文为3个学生,5顶帽子. 思维难度较大,作为引入不太合适,故改简单些.) 切入主题. |
|
二. 实例递进,形成概念 1. 推理的概念形成 幻灯片:生活中经常看到 (1) 天空乌云密布,燕子低飞,蚂蚁搬家,我们会想到什么? (2) 河面的冰融化,柳树发芽,草地泛青,我们又会想到什么? 提问:什么是推理?学生发言,教师点评. 总结:根据一个或几个已知的事实(或假设)来确定一个新的判断的思维方式就叫推理. 从结构上说,推理一般由前提和结论两部分构成的. 2. 合情推理的概念形成 幻灯片:下面哪些是推理? (1) 我国地质学家李四光发现中国松辽地区和中亚细亚的地质结构类似,而中亚细亚有丰富的石油,由此,他推断松辽平原也蕴藏着丰富的石油; (2) 1856年,法国微生物学家巴斯德发现乳酸杆菌能使啤酒变酸,接着他又发现细菌是引起蚕病的原因,据此,巴斯德推断人身上的一些传染病也是由细菌引起的; (3) 三角形的内角和为 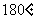 ,四边形的内角和为 ,四边形的内角和为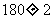 ,五边形的内角和为 ,五边形的内角和为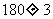 ,……,所以 ,……,所以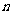 边形的内角和为 边形的内角和为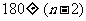 ; ;(4) 农谚说:瑞雪兆丰年. 提问分三步进行 一问:哪些是推理?学生发言,教师点评. 二问:上述推理所得结论是否一定正确? 总结:这种前提为真时,结论可能为真的推理,叫做合情推理. 三问:对比(1)、(3)这两个推理,你能发现它们的相同点和不同点吗? 3. 归纳推理的概念形成 幻灯片:看下面的例子,试写出一般性结论. (1) 1+3=4; 1+3+5=9; 1+3+5+7=16. (2) 一元一次方程有一个实数根; 一元二次方程最多有两个实数根; 一元三次方程最多有三个实数根. 提问:什么是归纳推理?学生发言,教师点评. 总结:根据一类事物的部分对象具有某种性质,推出该类事物的所有对象都具有这种性质的推理, 称为归纳推理(简称归纳). 回顾给出定义的过程,其本身就是归纳(从特殊到一般)的过程,所以可以说“我们归纳出了归纳”. (这两个“归纳”上有点区别,第一个重在归纳总结,第二个才是归纳推理.) |
从学生熟悉的生活经验出发,让学生体会推理的含义,逐步总结其定义. 引导学生归纳出推理的概念. 生活与数学结合的实例,使学生体会合情推理的含义,对各种推理有初步认识. 一问的目的是:巩固推理的概念. 二问的目的是:引导学生归纳合情推理的概念. 三问的目的是:引出归纳推理(不必出现类比推理这个名词). 纯数学的实例,使学生体会归纳推理的含义. 引导学生概括归纳推理的概念. 现学现用,而且这句话本身很有趣,有利于激发学生的兴趣. |
|
三. 经典探究,深化新知 幻灯片:汉诺塔问题  如图,有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上. (1) 每次只能移动1个金属片; (2) 较大的金属片不能放在较小的金属片上面. 试推测:把 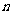 个金属片从1号针移到3号针,最少需要移动多少次? 个金属片从1号针移到3号针,最少需要移动多少次?师生互动、生生合作 1. 安排学生分组讨论,动手实践; 教师可事先准备一些硬币或圆纸片,但又故意不够数量,让喜欢动手的学生领取实物操作,让喜欢动脑的学生思考:在没有实物的情况下,如何简捷地表示移动过程,这本身就值得动动脑筋. 2. 学生发言,教师点评; 3. 鼓励学生课下完成证明. 总结归纳推理的一般步骤: (1) 通过观察个别情况发现某些相同性质; (2) 从已知的相同性质中推出一个明确表述的一般性命题(猜想). |
汉诺塔问题的探索,完整体现了归纳推理的过程,很具有代表性.使学生充分体验从个别情况看起,发现规律,归纳总结,做出推理的完整经过. 考虑到学生能力上的差异,鼓励他们采用不同的处理办法,爱动手的多实践,爱动脑的多思考. 证明不是本节课需要解决的问题,故课上不做要求,鼓励学生课后尝试完成. |
|
四. 习题演练,巩固提升 1. 应用归纳推理猜测 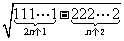 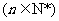 的值. 的值.答:归纳发现 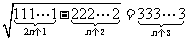 . .2. 设 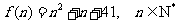 ,计算 ,计算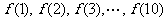 的值,并归纳一般性结论. 的值,并归纳一般性结论.练习2的处理: (1) 计算发现 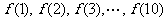 都是质数,但由此归纳推理得 都是质数,但由此归纳推理得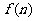 为质数确是错误的. 为质数确是错误的.(2) 题目本身是开放的,还可以得出很多结论,比如都是奇数,相邻项之差为等差数列,等等. 鼓励同学给出自己的结论,但要引导他们得出更深刻的结论. |
通过练习,巩固归纳推理的步骤,进一步学习其用法. 所选两题分别为教材课后习题和课堂例题.力争把教材用好用足. 强调归纳推理所得的结论不一定正确. 此为教材例题,这里把它改为开放题处理似乎更合适. |
|
五. 引导小结,设疑再思 1. 回顾小结 (1) 引导学生从知识、方法、收获三个方面进行小结,明确推理、合情推理、归纳推理的概念及彼此间关系. (2) 以问题的方式引导学生思考“推理”与“证明”的关系,加深对概念的理解,强调推理的作用. 2. 布置作业:课本P56练习A、B. |
回顾小结. 提高认识 (引导学生从“推理结论是否正确”和“推理的作用”两个方面理解它们之间的差异). |
2. 培养学生的归纳探索能力,提高学生的创新意识.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com