
4. 王 维《使至塞上》
单车欲问边,属国过居延。征蓬出汉塞,归雁入胡天。
大漠孤烟直,长河落日圆。萧关逢候骑,都护在燕然。
3. 辛弃疾《破阵子·醉里挑灯看剑》
醉里挑灯看剑,梦回吹角连营。八百里分麾下炙,五十弦翻塞外声。沙场秋点兵。
马作的卢飞快,弓如霹雳弦惊。了却君王天下事,赢得生前身后名。可怜白发生!
2. 周敦颐《爱莲说》
水陆草木之花,可爱者甚蕃。晋陶渊明独爱菊;自李唐来,世人甚爱牡丹;予独爱莲之出淤泥而不染,濯清涟而不妖,中通外直,不蔓不枝,香远益清,亭亭净植,可远观而不可亵玩焉。
予谓菊,花之隐逸者也;牡丹,花之富贵者也;莲,花之君子者也。噫!菊之爱,陶后鲜有闻;莲之爱,同予者何人;牡丹之爱,宜乎众矣!
1.[孔子语录]
※ 子曰:“学而时习之,不亦说乎?有朋自远方来,不亦乐乎?人不知而不愠,不亦君子乎?”
※ 子曰:“温故而知新,可以为师矣。”
※ 子曰:“学而不思则罔;思而不学则殆。”
※ 子曰:“由!诲女知之乎!知之为知之,不知为不知,是知也。”
※ 子贡问曰:“孔文子何以谓之‘文’也?”子曰:“敏而好学,不耻下问,是以谓之‘文’也。”
※ 子曰:“默而识之,学而不厌,诲人不倦,何有于我哉!”
※ 子曰:“三人行,必有我师焉;择其善者而从之,其不善者而改之。”
※ 子曰:“不愤不启,不悱不发。举一隅不以三隅反,则不复也。
|
教学环节 |
教学过程 |
师生互动 |
设计思想 |
|||||
|
情景 引入 |
多媒体展示: 材料1:地球围绕着太阳旋转; 材料2:“神舟六号”飞船升空录像. 引入课题:椭圆及其标准方程. |
师:引导学生观察轨道. 生:观察动画,指出地球与 “神六”的运行轨道. 师:板书课题. |
利用学生熟知的地理规律:地球围绕太阳转引入,让学生感到亲切自然;通过“神六”的升空录像,让学生感受现实,激发学生的兴趣,培养爱国思想. 通过做实验,让学生动手实践,体验椭圆的形成过程,加深对椭圆定义的理解. 将学生分为四人一组,通过分组讨论、研究,增强学生的合作意识. |
|||||
|
学 习 探 究 (一) |
动手实验: (1) 取一定长的细绳,把它的两个 端点固定在黑板的同一点处,套上 铅笔,拉紧绳子,旋转一周,会得 到什么图形? (2) 把绳子的两个端点拉开一段距 离,再套上铅笔旋转,又会得到什 么图形? (3) 继续拉远两个端点的距离,直 到把绳子拉直,又会得到什么图形? |
实验(1)教师演示,学生观 察思考. 实验(2)、(3),各小组学生利 用手中工具在图板上进行实验. |
||||||
|
归纳总结: 当绳长大于两定点的距离时, 轨迹是椭圆; 当绳长等于两定点的距离时, 轨迹是以这两个定点为端点的线段; 当绳长小于两定点的距离时, 没有轨迹. |
师:引导学生讨论实验结果,总结规律. 生:小组讨论,相互补充, 得出结论. |
|||||||
|
教学环节 |
教学过程 |
师生互动 |
设计思想 |
|||||
|
学 习 探 究 (一) |
多媒体展示: 椭圆形成过程. 利用点的轨迹,描述椭圆的定义. 椭圆的定义:平面内与两个定点 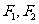 的距离的和等于常数(大于 的距离的和等于常数(大于 )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两个定点的距离叫做焦距. )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两个定点的距离叫做焦距.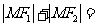 常数(大于 常数(大于 ) ) |
师:引导学生观察椭圆形成过程,找出动点、定点及绳长是否变化,组织小组讨论. 生:小组讨论,给出椭圆 定义. 师:设动点为M,椭圆的定义可用什么式子表示? |
通过学生观察、思考、讨论,概括出椭圆的定义,让学生全程参与概念的探究过程,加深理解,提高概括能力和数学语言的表达能力. 建立椭圆的方程是本节课的难点,为降低难度,让学生回顾求曲线方程的步骤,以已有的知识来探求新的知识,温故知新,教师再加以正确的引导,新知会自然形成. |
|||||
|
学 习 探 究 (二) |
下面我们来建立椭圆的方程 建系:以 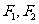 所在的直线为x轴,以线段F1F2的垂直平分线为y轴建立直角坐标系xOy. 所在的直线为x轴,以线段F1F2的垂直平分线为y轴建立直角坐标系xOy.设点:设点M(x,y)是椭圆上的任意一点,点M到 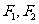 的距离和为2a,焦距为2c(c>0),则F1(-c,0), F2(c,0) 的距离和为2a,焦距为2c(c>0),则F1(-c,0), F2(c,0)列式:由定义: 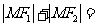 2a, 2a,即 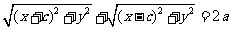 化简:整理,得 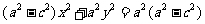 ∵a>0,c>0,2a>2c ∴ 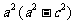 >0. >0.方程的两边都除以 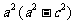 ,得 ,得 |
生:回顾求曲线方程的步骤:⑴建系,⑵设点,⑶列式,⑷化简. 师:引导学生按求曲线方程的步骤建立椭圆的方程. 生:思考,回答: (1)怎样建立适当的坐标系 (2)如何设点? (3)怎样列式? (4)如何化简? 生:分析化简的方法,在练习本上完成化简. |
||||||
|
教学环节 |
教学过程 |
 师生互动 师生互动 |
设计思想 |
||||
|
学 习 探 究 (二) |
 . .   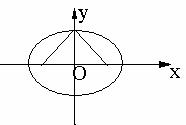 如图: 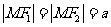 , ,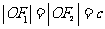 则 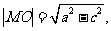  令 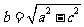 ,则 ,则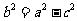 ,那么方程变为: ,那么方程变为: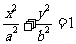 (a>b>0). (a>b>0). |
师:请同学们在图中找出长度等于a,c的线段,则 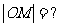 师:引导学生推出椭圆的标准方程. 师:指出其焦点在x轴上,坐标为F1(-c,0),F2(c,0) 生:观察图像,识记方程. |
椭圆的标准方程的导出,放手给学生有很大的难度,这里采取有意义的接受学习的 方式,教师对照图形,加以引导,让学生明白方程中字母的几何意义,对方程的理解有很大的作用. 展示动画,通过类比的方法,让学生对照焦点在x轴的情形,写出焦点在y轴上时,椭圆的标准方程. 通过图表便于对比,加深学生对两个方程及几何意义的认识. 尝试练习,加深对方程及几何意义的理解. |
||||
|
多媒体展示动画: 将椭圆的焦点放在y轴上 结论:当焦点在y轴是时,椭圆的方程为: 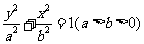 . .多媒体展示图表: 让学生对照图形、方程理解记忆. |
师:若焦点放在y轴上,方程又怎样 ? 生:小组讨论椭圆的方程,相互交流、补充,得出结论. 生:分析方程、图形,识记椭圆的标准方程. 师:引导学生如何根据方程判断焦点的位置? |
||||||
|
实 践 体 验 |
1、你能判断下列椭圆的焦点位置吗?并写出焦点坐标. (1) 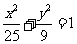 ; ; (2) 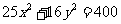 . . |
生:根据所学椭圆的标 准方程,思考后回答. 师生共同矫正. 生:总结如何判断焦点 的位置? |
|||||
|
教学环节 |
教学过程 |
师生互动 |
设计思想 |
|||||
|
实 践 体 验 |
2、请你写出符合下列条件的椭圆的标准方程: (1) a=4,b=1,焦点在x轴上; (2) a=4,c= 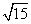 ,焦点在y轴上. ,焦点在y轴上.
|
生:练习本上完成后回答. 师:指出求椭圆的关键是求a和b的值,a、b、c的关系是  . . |
通过练习,加深学生对a、b、c的理解和对公式的记忆. 让学生分析阐述解法,训练语言表达能力,提高分析问题的能力。 让学生板演,规范学生的解题步骤. 通过解题后的反思,增强学生的反思意识,有利于总结方法规律. 体验高考,提高学生的学习兴趣,增强学习的信心. 回顾反思本课时所学知识,梳理巩固所学内容. |
|||||
|
学 以 致 用 |
例1 已知椭圆的两个焦点坐标分别为(-2,0),(2,0),并且椭圆经过点( 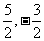 ),求它的标准方程. ),求它的标准方程. |
生:分析题意,寻求解法. 师:正确地引导学生. 生:一生板演,其它学生做在练习本上. 师生共同矫正. 生:思考是否还有其它解法?发表见解. 总结方法:(1)定义法(2)待定系数法. |
||||||
|
体 验 高 考 |
(全国)已知椭圆 上一点P到椭圆的一焦点的距离为3,则P到另一焦点的距离为( ) 上一点P到椭圆的一焦点的距离为3,则P到另一焦点的距离为( )A、2 B、3 C、5 D、7 |
生:思考,解决,体验高考. |
||||||
|
课 堂 小 结 |
多媒体展示: (1)椭圆的定义; (2)椭圆的标准方程(图形、焦点坐标、标准方程、a、b、c的关系). |
生:总结本节课所学及收获. 师:课件展示所学内容. |
||||||
2.2.1椭圆及其标准方程 一、椭圆的定义 方程的推导 一、椭圆的定义 方程的推导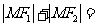 常数(大于 常数(大于 ) ) 二、椭圆的标准方程 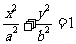 (a>b>0) 学生板演区域 (a>b>0) 学生板演区域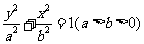 |
重点:掌握椭圆的定义及标准方程,理解坐标法的基本思想;
难点:椭圆标准方程的推导与化简.
3、情感态度与价值观目标:
通过小组合作,培养学生的协作、友爱精神,体验成功的快乐.
1、知识与技能目标
(1)理解椭圆的定义及焦点、焦距的概念,能正确推导椭圆的标准方程;
(2)掌握求椭圆标准方程的定义法和待定系数法;
4、(08江苏7)某地区为了解70~80岁老人的日平均睡眠时间
(单位:h),现随机地选择50位老人做调查,下表是
50位老人日睡眠时间频率分布表:
|
序号 (i) |
分组 睡眠时间 |
组中值 (Gi) |
频数 (人数) |
频率 (Fi) |
|
1 |
[4,5) |
4.5 |
6 |
0.12 |
|
2 |
[5,6) |
5.5 |
10 |
0.20 |
|
3 |
[6,7) |
6.5 |
20 |
0.40 |
|
4 |
[7,8) |
7.5 |
10 |
0.20 |
|
5 |
[8,9] |
8.5 |
4 |
0.08 |
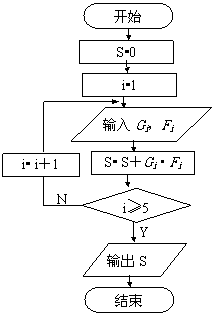 在上述统计数据的分析中,一部分计算见算法流程图,
在上述统计数据的分析中,一部分计算见算法流程图,
则输出的S的值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com