
1、2、6、核能
①核能
原子核的半径很小,其中质子间的库仑力是很大的。然而通常的原子核却是很稳定的。这说明原子核里的核子之间一定存在着另一种和库仑力相抗衡的吸引力,这种力叫核力。
从实验知道,核力是一种强相互作用,强度约为库仑力的确100倍。核力的作用距离很短,只在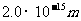 的短距离内起作用。超过这个距离,核力就迅速减小到零。质子和中子的半径大约是
的短距离内起作用。超过这个距离,核力就迅速减小到零。质子和中子的半径大约是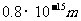 ,因此每个核子只跟它相邻的核子间才有核力的作用。核力与电荷无关。质子和质子,质子和中子,中子和中子之间的作用是一样的。当两核子之间的距离为
,因此每个核子只跟它相邻的核子间才有核力的作用。核力与电荷无关。质子和质子,质子和中子,中子和中子之间的作用是一样的。当两核子之间的距离为 时,核力表现为吸力,在小于
时,核力表现为吸力,在小于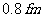 时为斥力,在大于10fm时核力完全消失。
时为斥力,在大于10fm时核力完全消失。
②质能方程
爱因斯坦从相对论得出物体的能量跟它的质量存在正比关系,即
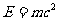
这个方程叫做爱因斯坦质能方程,式中c是真空中的光速,m是物体的质量,E是物体的能量。如果物体的能量增加了△E,物体的质量也相应地增加了△m,反过来也一样。△E和△m之间的关系符合爱因斯坦的质能方程。

③质量亏损
原子核由核子所组成,当质子和中子组合成原子核时,原子核的质量比组成核的核子的总质量小,其差值称为质量亏损。用m表示由Z个质子、Y个中子组成的原子核的质量,用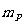 和
和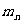 分别表示质子和中子的质量,则质量亏损为:
分别表示质子和中子的质量,则质量亏损为:
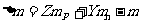
④原子核的结合能和平均结合能
由于核力将核子聚集在一起,所以要把一个核分解成单个的核子时必须反对核力做功,为此所需的能量叫做原子核的结合能。它也是单个核子结合成一个核时所能释放的能量。根据质能关系式,结合能的大小为:

原子核中平均每个核子的结合能称为平均结合能,用N表示核子数,则:
平均结合能=
平均结合能越大,原子核就越难拆开,平均结合能的大小反映了核的稳定程度。从平均结合能曲线可以看出,质量数较小的轻核和质量数级大的重核,平均结合能都比较小。中等质量数的原子核,平均结合能大。质量数为50~60的原子核,平均结合能量大,约为8.6MeV。
1、2、5、原子核的组成
用人工的方法使原子核发生变化,是研究原子核结构及变化规律的有力武器。确定原子核的组成有赖于质子和中子的发现。
1919年,卢瑟福用α粒子轰击氮原子核而发现了质子,这个变化的核反应方程:
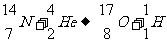
1932年,查德威克用α粒子轰击铍原子核而发现了中子,这个变化的核反应方程是:
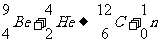
通过以上实验事实,从而确定了原子核是由质子和中子组成的,质子和中子统称为核子。某种元素一个原子的原子核中质子与中子的数量关系为:
质子数=核电荷数=原子序数
中子数=核质量数-质子数
具有相同质子数不同中子数的原子互称为同位素,利用放射性同位素可作“示踪原子”,用其射线可杀菌、探伤、消除静电等。
1.2.4、衰变定律和半衰期
研究发现,任何放射性物质在单独存在时,都遵守指数衰减规律
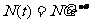 ①
①
这叫衰变定律。式中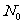 是t=0时的原子核数目,N(t)是经时间t后还没有衰变的原子核的数目,λ叫衰变常数,对于不同的核素衰变常数λ不同。由上式可得:
是t=0时的原子核数目,N(t)是经时间t后还没有衰变的原子核的数目,λ叫衰变常数,对于不同的核素衰变常数λ不同。由上式可得:
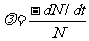 ②
②
式中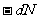 代表在
代表在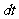 时间内发生的衰变原子核数目。分母N代表t时刻的原子核总数目。λ表示一个原子核在单位时间内发生衰变的概率。不同的放射性元素具有不同的衰变常数,它是一个反映衰变快慢的物理量,λ越大,衰变越快。
时间内发生的衰变原子核数目。分母N代表t时刻的原子核总数目。λ表示一个原子核在单位时间内发生衰变的概率。不同的放射性元素具有不同的衰变常数,它是一个反映衰变快慢的物理量,λ越大,衰变越快。
半衰期表示放射性元素的原子核有半数发生衰变所需的时间。用T表示,由衰变定律可推得:
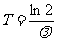 ③
③
半衰期T也是反映衰变快慢的物理量;它是由原子核的内部因素决定的,而跟原子所处的物理状态或化学状态无关;半衰期是对大量原子核衰变的统计规律,不表示某个原子核经过多长时间发生的衰变。由①、③式则可导出衰变定律的另一种形式,即
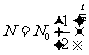 (T为半衰期,t表示衰变的时间,
(T为半衰期,t表示衰变的时间,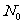 表示衰变前原子核的总量,N表示t后未衰变的原子核数)
表示衰变前原子核的总量,N表示t后未衰变的原子核数)
或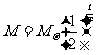 (
(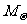 为衰变前放射性物质的质量,M为衰变时间t后剩余的质量)。
为衰变前放射性物质的质量,M为衰变时间t后剩余的质量)。
1.2.3、原子核的衰变
放射性元素的原子核放出某种粒子后,变成另一种新核的现象,叫做原子核的衰变,衰变过程遵循电荷守恒定律和质量守恒定律。用X表示某种放射性元素,z表示它的核电荷数,m表示它的质量数,Y表示产生的新元素,中衰变规律为:
α衰变:通式 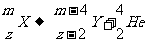
例如 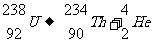
β衰变:通式 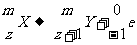
例如 
γ衰变:通式 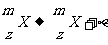 (γ射线伴随着α射线、β射线同时放出的。原子核放出γ射线,要引起核的能量发生变化,而电荷数和质量数都不改变)
(γ射线伴随着α射线、β射线同时放出的。原子核放出γ射线,要引起核的能量发生变化,而电荷数和质量数都不改变)
1.2.2、天然放射现象
天然放射性元素的原子核,能自发地放出射线的现象,叫天然放射现象。这一发现揭示了原子核结构的复杂性。天然放射现象中有三种射线,它们是:
α射线:速度约为光速的1/10的氦核流(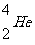 ),其电离本领很大。
),其电离本领很大。
β射线:速度约为光速的十分之几的电子流(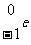 ),其电离本领较弱,贯穿本领较弱。
),其电离本领较弱,贯穿本领较弱。
γ射线:波长极短的电磁波,是伴随着α射线、β射线射出的,其电离本领很小,贯穿本领最强。
1.2.1、结合能
除氢核外,原子核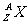 中Z个质子与(A-Z)个中子静质量之和都大于原子核的静质量
中Z个质子与(A-Z)个中子静质量之和都大于原子核的静质量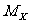 ,其间之差:
,其间之差:

称为原子核的质量亏损。式中、分别为质子、中子的静质量。造成质量亏损的原因是核子相互吸引结合成原子核时具有负的能量,这类似于电子与原子核相互吸引力结合成原子时具有负的能量(例如氢原子处于基态时电子轨道能量为-13.6eV)。据相对论质能关系,负能量对应质量亏损。质量亏损折合成的能量:
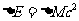
称为原子核的结合能,注意结合能取正值。结合能可理解成为了使原子核分裂成各个质子和中子所需要的外加你量。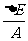 称为核子的平均结合能。
称为核子的平均结合能。
1、1.4、玻尔理论的局限性:
玻尔原子理论满意地解释了氢原子和类氢原子的光谱;从理论上算出了里德伯恒量;但是也有一些缺陷。对于解释具有两个以上电子的比较复杂的原子光谱时却遇到了困难,理论推导出来的结论与实验事实出入很大。此外,对谱线的强度、宽度也无能为力;也不能说明原子是如何组成分子、构成液体个固体的。玻尔理论还存在逻辑上的缺点,他把微观粒子看成是遵守经典力学的质点,同时,又给予它们量子化的观念,失败之处在于偶保留了过多的经典物理理论。到本世纪20年代,薛定谔等物理学家在量子观念的基础上建立了量子力学。彻底摒弃了轨道概念,而代之以几率和电子云概念。
例题1:设质子的半径为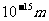 ,求质子的密度。如果在宇宙间有一个恒定的密度等于质子的密度。如不从相对论考虑,假定它表面的“第一宇宙速度”达到光速,试计算它的半径是多少。它表面上的“重力加速度”等于多少?(1mol气体的分子数是
,求质子的密度。如果在宇宙间有一个恒定的密度等于质子的密度。如不从相对论考虑,假定它表面的“第一宇宙速度”达到光速,试计算它的半径是多少。它表面上的“重力加速度”等于多少?(1mol气体的分子数是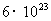 个;光速
个;光速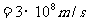 );万有引力常数G取为
);万有引力常数G取为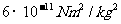 。只取一位数做近似计算。
。只取一位数做近似计算。
解: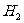 的摩尔质量为2g/mol,
的摩尔质量为2g/mol,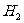 分子的质量为
分子的质量为
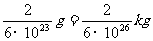
∴质子的质量近似为 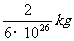
质子的密度 ρ=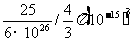 =
=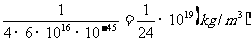
设该星体表面的第一宇宙速度为v,由万引力定律,得
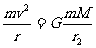 ,
,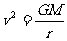
而 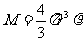
∴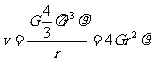
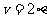
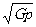
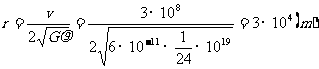
由于“重力速度”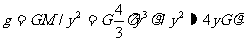
∴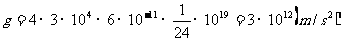
[注]万有引力恒量一般取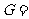 6.67
6.67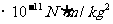
例题2:与氢原子相似,可以假设氦的一价正离子(He )与锂的二价正离子(L
)与锂的二价正离子(L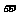 )核外的那一个电子也是绕核作圆周运动。试估算
)核外的那一个电子也是绕核作圆周运动。试估算
(1)He 、L
、L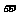 的第一轨道半径;
的第一轨道半径;
(2)电离能量、第一激发能量;
(3)赖曼系第一条谱线波长分别与氢原子的上述物理量之比值。
解:在估算时,不考虑原子核的运动所产生的影响,原子核可视为不动,其带电量用+Ze表示,可列出下面的方程组:
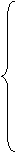
 , ①
, ①
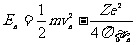 , ②
, ②
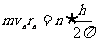 ,n=1,2,3,… ③
,n=1,2,3,… ③
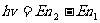 , ④
, ④
由此解得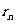 ,
, ,并可得出
,并可得出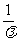 的表达式:
的表达式:
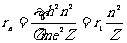 , ⑤
, ⑤
其中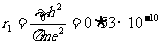 米,为氢原子中电子的第度轨道半径,对于He
米,为氢原子中电子的第度轨道半径,对于He ,Z=2,对于Li
,Z=2,对于Li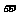 ,Z=3.
,Z=3.
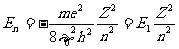 , ⑥
, ⑥
其中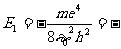 13.6电子伏特为氢原子的基态能.
13.6电子伏特为氢原子的基态能.
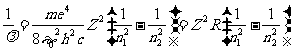 . ⑦
. ⑦
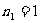 ,2,3,…
,2,3,…
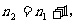
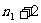 ,
,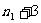 ,…
,…
R是里德伯常数。
(1)由半径公式⑤,可得到类氢离子与氢原子的第一轨道半径之比:
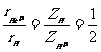 ,
,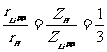 .
.
(2)由能量公式⑥,可得到类氢离子与氢原子的电离能和第一激发能(即电子从第一轨道激发到第二轨道所需的能量)之比:
电离能:  ,
,
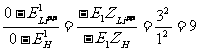
第一激发能:
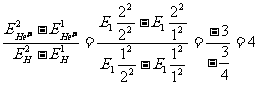 ,
,
 。
。
(其中: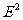 表示电子处在第二轨道上的能量,
表示电子处在第二轨道上的能量,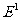 表示电子处在第一轨道上的能量)
表示电子处在第一轨道上的能量)
(3)由光谱公式⑦,氢原子赖曼系第一条谱线的波长有:
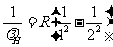
相应地,对类氢离子有:
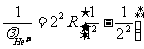 ,
,
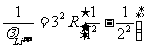 ,
,
因此 :
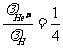 ,
, 。
。
例3:已知基态He 的电离能为E=54.4Ev,(1)为使处于基态的He
的电离能为E=54.4Ev,(1)为使处于基态的He 进人激发态,入射光子所需的最小能量应为多少?(2)He
进人激发态,入射光子所需的最小能量应为多少?(2)He 从上述最底激发态跃迁返回基态时,如考虑到该离子的反冲,则与不考虑反冲相比,它所发射的光子波长的百分变化有多大?(离子He
从上述最底激发态跃迁返回基态时,如考虑到该离子的反冲,则与不考虑反冲相比,它所发射的光子波长的百分变化有多大?(离子He 的能级En与n的关系和氢原子能级公式类中,可采用合理的近似。)
的能级En与n的关系和氢原子能级公式类中,可采用合理的近似。)
分析:第(1)问应正确理解电离能概念。第(2)问中若考虑核的反冲,应用能量守恒和动量守恒,即可求出波长变化。
解:(1)电离能表示He 的核外电子脱离氦核的束缚所需要的能量。而题问最小能量对应于核外电子由基态能级跃迁到第一激发态,所以
的核外电子脱离氦核的束缚所需要的能量。而题问最小能量对应于核外电子由基态能级跃迁到第一激发态,所以
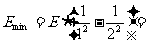 54.4
54.4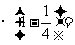 40.8eV
40.8eV
(2)如果不考虑离子的反冲,由第一激发态迁回基态发阜的光子有关系式:
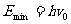
现在考虑离子的反冲,光子的频率将不是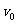 而是
而是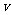 ,
,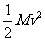 为反冲离子的动能,则由能量守恒得
为反冲离子的动能,则由能量守恒得 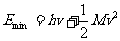
又由动量守恒得 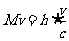
式中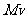 是反冲离子动量的大小,而
是反冲离子动量的大小,而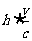 是发射光子的动量的大小,于是,波长的相对变化
是发射光子的动量的大小,于是,波长的相对变化
 =
=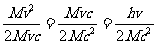
由于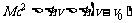
所以 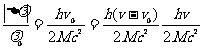
代入数据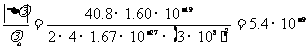
即百分变化为0.00000054%
§1、2 原子核
原子核所带电荷为+Ze,Z是整数,叫做原子序数。原子核是由质子和中子组成,两者均称为核子,核子数记为A,质子数记为Z,中子数便为A-Z。原子的元素符号记为X,原子核可表述为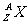 ,元素的化学性质由质子数Z决定,Z相同N不同的称为同位素。
,元素的化学性质由质子数Z决定,Z相同N不同的称为同位素。
在原子物理中,常采用原子质量单位,一个中性碳原子质量的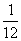 记作1个原子单位,即lu=
记作1个原子单位,即lu=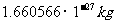 。质子质量:
。质子质量: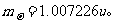 中子质量:
中子质量: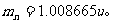 电子质量:
电子质量: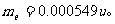
2、里德伯公式
1896年,瑞典的里德伯把氢原子光谱的所有谱线的波长用一个普遍的经验公式表示出来,即
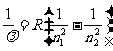 n=1,2,3…
n=1,2,3…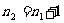 ,
,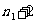 ,
,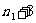 …
…
上式称为里德伯公式。对每一个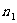 ,上是可构成一个谱线系:
,上是可构成一个谱线系:
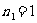 ,
,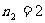 ,3,4… 莱曼系(紫外区)
,3,4… 莱曼系(紫外区)
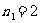 ,
,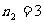 ,4,5… 巴耳末系(可见光区)
,4,5… 巴耳末系(可见光区)
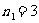 ,
,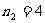 ,5,6… 帕邢系(红外区)
,5,6… 帕邢系(红外区)
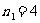 ,
,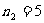 ,6,7… 布拉开系(远红外区)
,6,7… 布拉开系(远红外区)
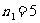 ,
,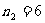 ,7,8… 普丰德系(远红外区)
,7,8… 普丰德系(远红外区)
以上是氢原子光谱的规律,通过进一步的研究,里德伯等人又证明在其他元素的原子光谱中,光谱线也具有如氢原子光谱相类似的规律性。这种规律性为原子结构理论的建立提供了条件。
1、巴耳末公式
研究原子的结构及其规律的一条重要途径就是对光谱的研究。19世纪末,许多科学家对原子光谱已经做了大量的实验工作。第一个发现氢原子线光谱可组成线系的是瑞士的中学教师巴耳末,他于1885年发现氢原子的线光谱在可见光部分的谱线,可归纳为如下的经验公式
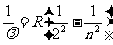 ,n=3,4,5,…
,n=3,4,5,…
式中的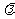 为波长,R是一个常数,叫做里德伯恒量,实验测得R的值为1.096776
为波长,R是一个常数,叫做里德伯恒量,实验测得R的值为1.096776 107
107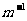 。上面的公式叫做巴耳末公式。当n=3,4,5,6时,用该式计算出来的四条光谱线的波长跟从实验测得的
。上面的公式叫做巴耳末公式。当n=3,4,5,6时,用该式计算出来的四条光谱线的波长跟从实验测得的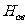 、
、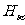 、
、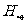 、
、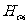 四条谱线的波长符合得很好。氢光谱的这一系列谱线叫做巴耳末系。
四条谱线的波长符合得很好。氢光谱的这一系列谱线叫做巴耳末系。
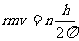 ,n=1、2……
,n=1、2……
其中m为电子质量,h为普朗克常量,这一条件表明,电子绕核的轨道半径是不连续的,或者说轨道是量子化的,每一可取的轨道对应一个能级。
定态假设意味着原子是稳定的系统,跃迁假设解释了原子光谱的离散性,最后由氢原子中电子轨道量子化条件,可导出氢原子能级和氢原子的光谱结构。
氢原子的轨道能量即原子能量,为 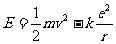
因圆运动而有
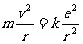
由此可得
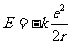
根据轨道量子化条件可得:
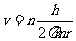 ,n=1,2……
,n=1,2……
因 ,便有
,便有
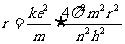
得量子化轨道半径为:
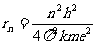 ,n=1,2……
,n=1,2……
式中已将r改记为rn对应的量子化能量可表述为:
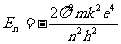 ,n=1,2……
,n=1,2……
n=1对应基态,基态轨道半径为 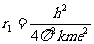
计算可得:
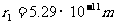 =0.529
=0.529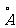
r1也称为氢原子的玻尔半径
基态能量为
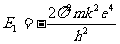
计算可得:
E1=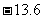 eV。
eV。
对激发态,有:
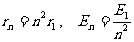 ,n=1,2…
,n=1,2…
n越大,rn越大,En也越大,电子离核无穷远时,对应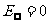 ,因此氢原子的电离能为:
,因此氢原子的电离能为:
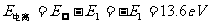
电子从高能态En跃迁到低能态Em辐射光子的能量为:
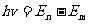
光子频率为
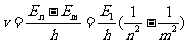 ,
,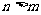
因此氢原子光谱中离散的谱线波长可表述为:
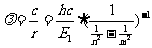 ,
,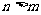
试求氢原子中的电子从第n轨道迁跃到n-1第轨道时辐射的光波频率,进而证明当n很大时这一频率近似等于电子在第n轨道上的转动频率。
辐射的光波频率即为辐射的光子频率 ,应有
,应有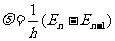
将
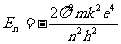
代入可得
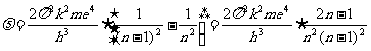
当n很大时,这一频率近似为 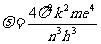
电子在第n轨道上的转动频率为:
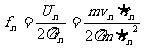
将
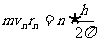
代入得
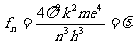
因此,n很大时电子从n第轨道跃迁到第n-1轨道所辐射的光波频率,近似等于电子在第n轨道上的转动频率,这与经典理论所得结要一致,据此,玻尔认为,经典辐射是量子辐射在 时的极限情形。
时的极限情形。
1、1.3、氢原子光谱规律
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com