
6、音调、响度与音品为乐音三要素。
音调-基音频率的高低,基频高则称音调高。人们对音调的感觉客观上也取决于声源振动的频率,频率高,感觉音调高。
响度-声音的强弱。声源振幅大、声音的声强(单位时间内通过垂直于声波传播方向的单位面积的能量)也大,人感觉到的声音也大。
音品-音色,它反映了不同声源发出的声音具有不同的特色。音品由声音所包含的泛音的强弱和频率决定。
5、乐音噪声--好听、悦耳的声音叫乐音,嘈杂刺耳的声音叫噪声。乐音是由作周期性振动的声源发出的,嘈声是由做无规则非周期性振动的声源产生的。
5.5.7.声波
机械振动在空气中的传播称为声波。声波作用于人耳,产生声音感觉。人耳可闻声波频率是16~20000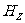 。频率超过20000
。频率超过20000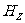 的声波叫超声波。超声波具有良好的定向性和贯穿能力。频率小于16
的声波叫超声波。超声波具有良好的定向性和贯穿能力。频率小于16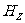 的声波称为次声波。在标准情况下,声波在空气中的速度为331m/s。
的声波称为次声波。在标准情况下,声波在空气中的速度为331m/s。
(1)声波的反射-声波遇障碍物而改变原来传播方向的现象。
回声和原来的声波在人耳中相隔至少0.1秒以上,人耳才能分辨,否则两种声音将混在一起,加强原声。
室内的声波,经多次反射和吸收,最后消失,这样声源停止发声后,声音还可在耳中继续一段时间,这段时间叫交混回响时间。交混回响时间太长,前后音互相重叠,分辨不清;交混时间太短,给人以单调不丰满的感觉,这种房间不适于演奏。
(2)声波的干涉--两列同频率同振幅的声波在媒质中相遇而发生的波干涉现象。
(3)声波的衍射--声波遇障碍物而发生的波衍射现象。由于声波波长在17cm-17m之间,与一般障碍物尺寸可相比拟,可绕过障碍物进行传播。而可见光的波长在0.4-0.8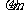 ,一般障碍物不能被光绕过去。这就是“闻其声而不见其人”的缘由。
,一般障碍物不能被光绕过去。这就是“闻其声而不见其人”的缘由。
(4)共鸣--声音的共振现象
音叉和空气柱可以发生共鸣。
在一个盛水的容器中插入一根玻璃管,在管口上方放一个正在发声的音叉,当把玻璃管提起和放下,以改变玻璃管中空气柱的长度时,便可以观察到空气柱与音叉发生共鸣的现象。在这个实验中发生共鸣的条件是: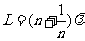 ,式中L为玻璃管的长度,
,式中L为玻璃管的长度,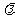 为音叉发出声波的波长,n为自然数。
为音叉发出声波的波长,n为自然数。
5.5.6、多普勒效应
站在铁路旁边听到车的汽笛声,发现当列车迎面而来时音调较静止时为高,而列车迅速离去时音调较静止时为低,此外,若声源静止而观察者运动,或者声源和观察者都运动,也会发生收听频率和声源频率不一致的现象,这种现象称为多普勒效应。下面分别探讨各种情况下多普勒频移的公式:
 (1)波源静止观察者运动情形
(1)波源静止观察者运动情形
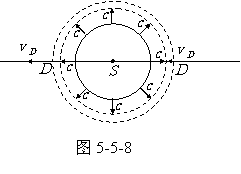
如图5-5-8所示,静止点波源发出的球面波波面是同心的,若观察者以速度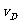 趋向或离开波源,则波动相对于观察者的传播速度变为
趋向或离开波源,则波动相对于观察者的传播速度变为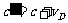 或
或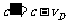 ,于是观察者感受到的频率为
,于是观察者感受到的频率为

从而它与波源频率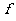 之比为
之比为
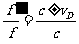
(2)波源运动观察者静止情形
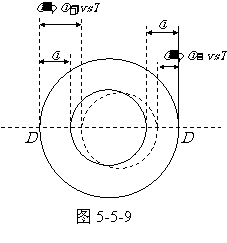
若波源以速度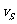 运动,它发出的球面波不再同心。图5-5-9所示两圆分别是时间相隔一个周期T的两个波面。它们中心之间的距离为
运动,它发出的球面波不再同心。图5-5-9所示两圆分别是时间相隔一个周期T的两个波面。它们中心之间的距离为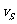 T,从而对于迎面而来或背离而去的观察者来说,有效的波长为
T,从而对于迎面而来或背离而去的观察者来说,有效的波长为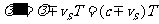
观察者感受到的频率为
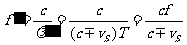
因而它与波源频率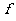 之比为
之比为
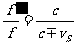
(3)波源和观察者都运动的情形
此处只考虑波的传播方向、波源速度、观察者速度三者共线的特殊情况,这时有效波速和波长都发生了变化,观察者感受到的频率为
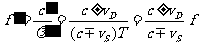
从而它与波源频率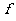 之比为
之比为
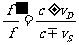
下举一个例
单行道上,有一支乐队,沿同一个方向前进,乐队后面有一坐在车上的旅行者向他们靠近。此时,乐队正在奏出频率为440HZ的音调。在乐队前的街上有一固定话筒作现场转播。旅行者从车上的收音机收听演奏,发现从前面乐队直接听到的声音和从广播听到的声音混合后产生拍,并测出三秒钟有四拍,车速为18km/h,求乐队前进速度。(声速=330m/s)。
解:先考虑车上听到的频率,连续两次应用多普勒效应,有

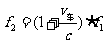 (
(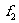 为旅行者听到乐队的频率)
为旅行者听到乐队的频率)
得 
收音机得到频率为
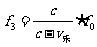 旅行者听到广播频率为
旅行者听到广播频率为
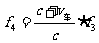
又拍频为 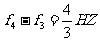 综上得:
综上得: =2.98m/s
=2.98m/s
5.6.5、驻波
驻波是频率相同、振幅相同、振动方向一致、传播方向相反的两列简谐波叠加的结果,如图6-5-6,设弦上传递的是连续的周期波,波源的振动方程为

向左传播的入射波表达式为
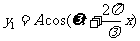
设波源到固定端的距离为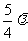 ,则入射波传到反射点时的相位为
,则入射波传到反射点时的相位为
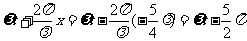
考虑到入射波和反射波在连接点的振动相位相反,即入射波在反射时产生了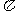 的相位突变,故反射波在反射点的相位为
的相位突变,故反射波在反射点的相位为
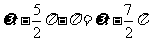
反射波在原点P的相位为
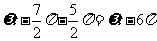
因而,反射波的波动方程为
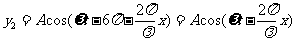
合成波为:
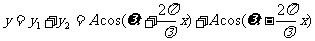
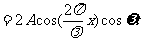
合成波的振幅为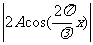 与x有 关,振幅最大处为波腹,振幅最小处为波节。波腹的位置为
与x有 关,振幅最大处为波腹,振幅最小处为波节。波腹的位置为
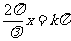
 即
即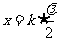
 如图5-6-6中的D、E、F等处。
如图5-6-6中的D、E、F等处。
波节的位置为
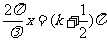
即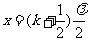

如图5-5-7中的O、A、B等处。
相邻两波节(或波腹)之间的间距为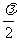 。
。
不同时刻驻波的波形如图5-6-7所示,其中实线表示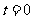 、T、2T……时的波形;点线表示
、T、2T……时的波形;点线表示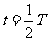 、
、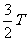 ……时的波形;点划线表示
……时的波形;点划线表示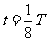 、
、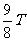 时的波形。
时的波形。
4、波的反射、折射和衍射
 当波在传播过程中遇到的两种介质的交界面时,一部分返回原介质中,称为反射波;另一部分将透入第二种介质继续传播,称为折射波,入射波的传播方向与交界面的法线成
当波在传播过程中遇到的两种介质的交界面时,一部分返回原介质中,称为反射波;另一部分将透入第二种介质继续传播,称为折射波,入射波的传播方向与交界面的法线成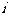 角,(
角,(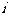 叫入射角),反射波的传播方向与交界面的法线成
叫入射角),反射波的传播方向与交界面的法线成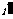 角(
角(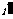 叫反射角)。折射波的传播方向与法线成
叫反射角)。折射波的传播方向与法线成 角(
角( 叫折射角),如图5-5-3,则有
叫折射角),如图5-5-3,则有

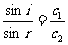
 式中
式中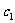 为波在入射介质中的传播速度,
为波在入射介质中的传播速度,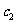 为波在折射介质中的传播速度,(1)式称为波的反射定律,(2)式称为波的折射定律。
为波在折射介质中的传播速度,(1)式称为波的反射定律,(2)式称为波的折射定律。
弦上的波在线密度不同的两种弦的连结点处要发生反射,反射的波形有所不同。
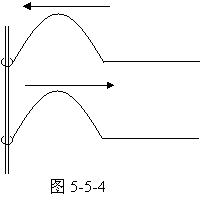
设弦上有一向上脉冲波,如图5-5-4,传到自由端以后反射,自由端可看成新的振源,振动得以继续延续下去,故反身波仍为向上的脉冲波,只是波形左右颠倒。当弦上有向上脉冲波经固定端反射时,固定端也可看成新的“振源”,由牛顿第三定律,固定端对弦的作用力方向与原脉冲对固定端的作用力方向相反,故反射脉冲向下,即波形不仅左、右颠倒,上、下也颠倒,这时反射波可看成入射波反向延伸的负值(如图5-5-5),将周期波看成一系列连续脉冲,周期波经自由端或固定端的反射也可由此得出。
波在传播过程中遇到障碍物时,偏离原来的传播方向,传到障碍物“阴影”区域的现象叫波的衍射。当障碍物或孔的尺寸比波长小,或者跟波长相差不多时,衍射现象比较明显;当障碍物或孔的尺寸比波长大的时候,衍射现象仍然存在,只是发生衍射的部分跟直进部分相比,范围较小,强度很弱,不够明显而已。此外,在障碍物或小孔尺寸一定的情况下,波长越长,衍射现象越明显。
3、波的叠加和干涉
当空间存在两个(或两个以上)振源发出的波时,空间任一点的扰动是各个波在该点产生的扰动的矢量和,这叫做波的叠加原理。
当有频率相同、振动方向相同的两列波在空间叠加时,会出现某些地方振动增强,某些地方振动减弱的现象,叫做波的干涉,这样的两列波叫相干波。
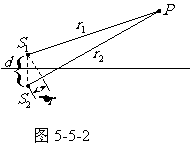
设有两列相干波自振源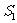 、
、 发出,两振源的位相相同,空间任一点P至
发出,两振源的位相相同,空间任一点P至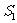 的距离为
的距离为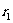 ,至
,至 的距离为
的距离为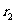 (图5-5-2),则两列波在P点产生的振动的相位差为
(图5-5-2),则两列波在P点产生的振动的相位差为

当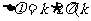 为整数),即当波程差
为整数),即当波程差
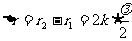 时,P点的合振动加强;
时,P点的合振动加强;
当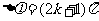 ,即当波程差
,即当波程差

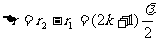 时,P点的合振动减弱,可见P点振动的强弱由波程差
时,P点的合振动减弱,可见P点振动的强弱由波程差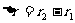 决定,是P点位置的函数。
决定,是P点位置的函数。
总之,当某一点距离两同位相波源的波程差等于零或者是波长的整数倍时,该点振动的合振幅最大,即其振动总是加强的;当某一点距离两同位波源的波程差等于半波长或半波长的奇数倍时,该点振动的合振幅最小,即其振动总是削弱的。
5.5.2、波动方程
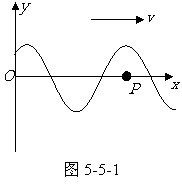 如图5-5-1所示,一列横波以速度
如图5-5-1所示,一列横波以速度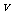 沿
沿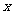 轴正方向传播,设波源O点的振动方程为:
轴正方向传播,设波源O点的振动方程为:

在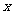 轴上任意点P的振动比O点滞后时间
轴上任意点P的振动比O点滞后时间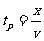 ,即当O点相位为
,即当O点相位为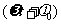 时,P点的相位为
时,P点的相位为 ,由
,由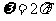 ,
,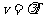 ,
,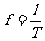 ,P点振动方程为
,P点振动方程为
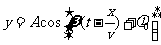
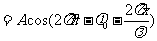
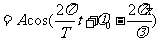
这就是波动方程,它可以描述平面简谐波的传播方向上任意点的振动规律。当波向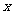 轴负方向传播时,(2)式只需改变
轴负方向传播时,(2)式只需改变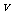 的正负号。由波动方程,可以
的正负号。由波动方程,可以
(1)求某定点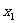 处的运动规律
处的运动规律
将 代入式(6-14),得
代入式(6-14),得
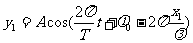
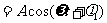
其中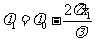 为
为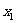 质点作简谐振动的初相位。
质点作简谐振动的初相位。
(2)求两点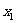 与
与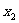 的相位差
的相位差
将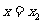 代入(2)式,得两点
代入(2)式,得两点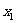 、
、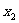 的相位差
的相位差
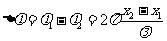
若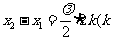 为整数),则
为整数),则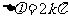 ,则该两点同相,它们的位移和速度都相同。若
,则该两点同相,它们的位移和速度都相同。若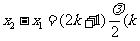 为整数),则
为整数),则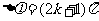 ,则该两点相位相反,它们的位移和速度大小相同,速度方向刚好相反。
,则该两点相位相反,它们的位移和速度大小相同,速度方向刚好相反。
球面波的波动方程与平面波相比,略有不同,对于球面波,其振幅随传播距离的增加而衰减,设离波源距离为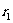 处的振幅为
处的振幅为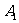 ,离波源距离为
,离波源距离为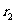 处的振幅为
处的振幅为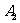 。则有
。则有
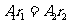
即振幅与传播的距离成反比
球面简谐波的方程为
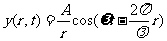
 式中A是与波源的距离为一个单位长度处的振幅。
式中A是与波源的距离为一个单位长度处的振幅。
5.5.1、机械波
机械振动在介质中的传播形成机械波,波传递的是振动和能量,而介质本身并不迁移。
自然界存在两种简单的波:质点振动方向与波的传播方向垂直时,称为横波;与传播方向一致时,叫纵波,具有切变弹性的介质能传播横波;具有体变弹性的介质可传播纵波,固体液体中可以同时有横波和纵波,而在气体中一般就只有纵波存在了。
在波动中,波上相邻两个同相位质点间的距离,叫做一个波长,也就是质点作一个全振动时,振动传播的距离。由于波上任一个质点都在做受迫振动,因此它们的振动频率都与振源的振动频率相等,也就是波的频率,在波动中,波长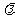 、频率
、频率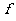 与传播速度
与传播速度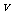 之间满足
之间满足
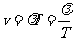 (1)
(1)
注意:波速不同于振动质点的运动速度,波速与传播介质的密度及弹性性质有关。
5.4.3、同频率相互垂直的两个简谐振动的合成
当一物体同时参与相互垂直的振动时
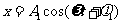
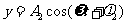
合振动的轨迹在直角坐标系中的方程为
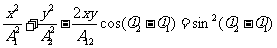 (6-17)
(6-17)
当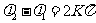 时,
时,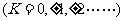

得
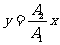
合成结果仍为简谐振动(沿斜率为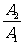 的直线作简谐振动)。
的直线作简谐振动)。
当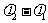 =
=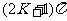 时,
时,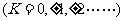
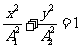
可见,当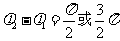 时,合振动均为椭圆振动,但两者旋转方向不同。
时,合振动均为椭圆振动,但两者旋转方向不同。
§5.5机械波
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com