
4.3.1、固液相变
①熔解物质从固态变成液态,叫做熔解。
对于晶体来说,熔解就是在一定的温度下进行的,该温度叫做这种晶体的熔点。晶体在熔解的过程中要吸收热量,但温度保持在其熔点不变,直至全部熔解为止。
对于大多数晶体,熔解时体积增大,但还有少数的晶体,如冰、铋、灰铸铁在熔解时体积反而缩小。
晶体的熔点与晶体的种类有关,对于同一种晶体,其熔点与压强有关。熔解时体积增大的物质,其熔点随压强的增加而增大,熔解时体积减小的物质,其熔点随压强的增大而减小。
晶体在熔解时,要吸收的热量,单位质量的某种物质,由固态熔解为液态时,所吸收的热量叫做物质的熔解热,记为λ,因此对质量为m的物体全部熔解所需吸收的热量
Q=λm。
②凝固物质由液相变为固相称为凝固。其中晶体的熔液凝固时形成晶体,这个过程又称为结晶。结晶的过程是无规则排列的粒子形成空间点阵的过程,在此期间,固、液两态平衡共存,温度保持不变。
在结晶过程中,单位质量的物质对外释放的热量称为凝固热。它与该物质在同温度下的熔解热相同。
4.2.3、空气的湿度
①空气的绝对湿度和相对湿度
由于地面水分的蒸发,空气中总会有水蒸气,而空气中所含水汽的多少就决定了空气的潮湿程度。
a、绝对湿度 空气中所含水气的分压强大小。
b、相对湿度 某温度时空气的绝对湿度跟同一温度下水的饱和气压的百分比。
如果B表示相对湿度,Pt表示绝对湿度,P表示同温度下饱和气的压强,则

空气干燥、潮湿程度直接决定于相对湿度,当相对湿度接近100%时,空气中水气接近饱和状态,水分难于蒸发,衣服晾不干,人也觉得十分烦闷,人体感到适中的相对湿度是60-70%。
②露点
 空气里的未饱和气在气温降低时会逐渐接近饱和,使空气里的水气恰好达到饱和时的温度,称为露点。
空气里的未饱和气在气温降低时会逐渐接近饱和,使空气里的水气恰好达到饱和时的温度,称为露点。
通过测定露点可以测出空气的湿度,因为当空气中水气的密度保持不变时,露点温度下的饱和水气压强就可以认为是空气的绝对湿度。
③露、霜、雾及其他
 大气中的水气在气温降低时也同样趋于饱和,白天温度较高时处于未饱和状态的水气,夜里气温下降时如达到露点或露点以下(0℃以上),则空气中水气将在树叶、草皮上凝结,这就是露。
大气中的水气在气温降低时也同样趋于饱和,白天温度较高时处于未饱和状态的水气,夜里气温下降时如达到露点或露点以下(0℃以上),则空气中水气将在树叶、草皮上凝结,这就是露。
如果空气中含有较多的尘埃或离子,达到饱和的水气将以尘埃或离子为中心凝结,这就形成雾,开启冰箱门,“冷气”所到之处,常达到露点以下,因此常形成为雾。
地面附近的空气中的水蒸气遇冷(0℃以下)而直接凝华的小冰粒,附着地面物体上成为霜。
湿度计是用来测量空气湿度的仪器。露点湿度计:它通过测定露点,然后查出该露点的饱和水气压和原温度的饱和水气压,即可求出相对湿度。干湿泡湿度计:它在一支温度计泡上包着纱布,纱布下端浸入水中。若空气中水气未饱和,湿纱布的水会蒸发,温度降低。这样湿泡温度计的温度值比干泡温度计的要低些。相对湿度越小,这个差值就越大。利用这个差值的大小可由表检查出空气的相对湿度。毛发湿度计:利用脱脂毛发长度的变化来控制指针偏转,直接指示相对湿度。
例:有一根玻璃毛线管,长为0.600m,内径2.00mm,内有50mm水银柱,水银柱把长细管分成两部分,一部分为真空,另一部分为空气和水气的混合物。倾斜管子,气室的长度可以变化,做实验时,改变倾斜度,得到数据如下表,符号在图4-2-3中示出。每次测量后,要等气体恢复平衡。求管内空气和水各有多少?
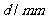 |
521 |
259 |
100 |
68 |
51 |
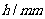 |
100 |
200 |
400 |
500 |
600 |
解:温度不变时,一定质量的理想气体遵循玻意耳定律,即压强p与体积V之间满足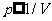 ,所以对本题表示数据的合适方法是作
,所以对本题表示数据的合适方法是作 图。对题中给定的数据适当变换得表格如下:
图。对题中给定的数据适当变换得表格如下:
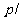  |
1.125 |
2.25 |
4.5 |
5.7 |
6.8 |
 |
0.611 |
1.23 |
3.18 |
4.69 |
6.25 |
利用这些数据作出 图线如图8-2-4所
图线如图8-2-4所
示,这样可发现数据分成两部分,一部分形成通过原点的直线,压强高时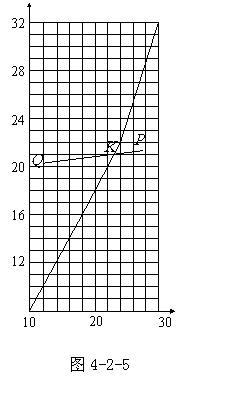 数据位于不通过原点的直线上,而只要是水汽没有饱和,水汽也可看作理想气体,当水汽开始凝结时,水汽分压是常数,而空气分压遵循玻意耳定律,这就是形成图示数据关系的原因。
数据位于不通过原点的直线上,而只要是水汽没有饱和,水汽也可看作理想气体,当水汽开始凝结时,水汽分压是常数,而空气分压遵循玻意耳定律,这就是形成图示数据关系的原因。
当水汽的分压 时,有
时,有
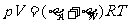
 或
或 ,其中γ为空气(A)或水(W)的摩尔数,另由
,其中γ为空气(A)或水(W)的摩尔数,另由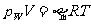 算出的
算出的 大于
大于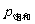 时,实际水气分压为
时,实际水气分压为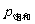 ,故满足于
,故满足于
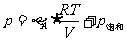
从图上将直线外延求得饱和蒸气压,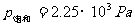 ,然后从标准饱和蒸气压表中查出温度,从图中的两条直线可得
,然后从标准饱和蒸气压表中查出温度,从图中的两条直线可得
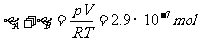

所以,管内空气和水分别有8.6μg的7.9μg。
说明因试题中没有给出温度T,另一个方法是可以假设室温为20℃,因为10℃的温度误差仅引起绝对温度3%的误差,不过这种方法相对于上面的解法相比则不是很好。
例:图4-2-5表示在10℃到30℃范围内水的饱和蒸气压曲线。现将温度为27℃、压强为1atm、相对湿度80%的空气封闭在某一容器中,把它逐渐冷却到12℃。试问:(1)这时空气的压强是多少?(2)温度降到多少时开始有水凝结?这时空气中所含的水蒸气为百分之几?
分析:本题并未给出水的饱和蒸气压随温度变化的函数关系,却提供了水的饱和蒸气压曲线,故用图解法求出水蒸气开始凝结时的温度及饱和蒸气压。显然在降温过程中,尚未凝结的水蒸气作等容变化。这时P与T成正比关系。但我们不妨设从27℃降到12℃过程中水蒸气一直作等容变化,该直线与饱和气由线交点就是水蒸气开始达到饱和时的状态,即图中K点,以后随着温度的降低水蒸气压沿饱和气曲线非线性变小。
解:(1)27℃水的饱和汽压27mmHg。 得水蒸气分压
得水蒸气分压 ,空气分压
,空气分压 。
。
设密闭容器中的空气冷却到12℃的空气分压为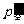 ,应用盖-吕萨克定律得
,应用盖-吕萨克定律得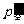 =701.5mmHg。此温度水蒸气分压
=701.5mmHg。此温度水蒸气分压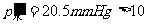 ℃水的饱和汽压10.3mmHg,故有部分水凝结,故12℃时的空气
℃水的饱和汽压10.3mmHg,故有部分水凝结,故12℃时的空气 =701.5+10.3=711.8mmHg。
=701.5+10.3=711.8mmHg。
(2)初态p点为27℃、21.6mmHg,末态点为12℃、20.5mmHg一直线交水的饱和汽压曲线K点为23.0℃、21.3mmHg,此时空气分压为728.1mmHg,这时空气中所含水蒸气百分比为 。
。
§4.3 固液相变与固气相变
4.2.2、气体的液化
我们知道,当饱和气的体积减小或温度降低时,它就可以凝结为液体,因此要使未饱和气液化,首先必须使之变成饱和气,方法有二:a、在温度不变的条件下,加大压强以减小未饱和气体积,相应就可以增大它的密度,直至达到该温度下饱和气的密度,从而把未饱和气变为饱和气;b、对较高温度下的未饱和气,在维持体积不变的条件下降低其温度,也可以使它变为在较低温度下的饱和气。
把未饱和气变为饱和气以后,只要继续减小其体积或降低其温度,多余的气就可凝结成液体。
但各种气体有一个特殊温度,在这个温度以上,无论怎样增大压强,都不能使它液化,这个温度就称为该气体的临界温度。
①气液转变的等温线
要使未饱和汽转变成饱和汽并使之液化,在等压条件下,气体通过降温可以转变为液体;在保持温度不变的条件下,通过增大压强减小体积的方式,也可以使气体液化。
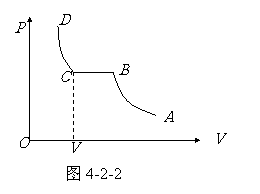 图4-2-2为某气体液化的过程曲线AB是液化以前气体的等温压缩过程,气体逐渐趋于饱和状态,B点对应于饱和汽状态,继续压缩就会出现液体;在液化过程BC中,压强
图4-2-2为某气体液化的过程曲线AB是液化以前气体的等温压缩过程,气体逐渐趋于饱和状态,B点对应于饱和汽状态,继续压缩就会出现液体;在液化过程BC中,压强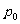 保持不变,气液化的总体积减小,BC过程中每一状态都是气液平衡共存的状态,因此
保持不变,气液化的总体积减小,BC过程中每一状态都是气液平衡共存的状态,因此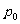 为这一温度下的饱和汽压。C点相当于气体全部液化时的状态;CD段就是液体的等温压缩过程。
为这一温度下的饱和汽压。C点相当于气体全部液化时的状态;CD段就是液体的等温压缩过程。
应该指出:由于各种气体都有一个特殊温度,在这个温度以上,无论怎样增大压强也不能使气体液化,这个温度称为临界温度。因此上述气液等温转变只能在气体的临界度以下进行。若等温转变时饱和汽密度为 ,BC段液体密度为
,BC段液体密度为 ,系统的总质量为m,当气液平衡共存时的体积为V,其中汽、液的体积分别是
,系统的总质量为m,当气液平衡共存时的体积为V,其中汽、液的体积分别是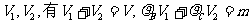 ,解得:
,解得: 。
。
②混合气的等温液化
混合气体的等温转变,应分解为各组分气体的等温转变过程来考虑不周。沸点不同的各组分气体,当等温压缩时,达到饱和开始液化的先后不同。同在1atm沸点高的气体,其饱和汽密度要小些,等温压缩它会先达到饱和开始液化。混合气体等温线的转折点,一定是某组分气体物态的转变点。
例:有一体积22.4L的密闭容器,充有温度 、压强3atm的空气和饱和水汽,并有少量的水;今保持温度
、压强3atm的空气和饱和水汽,并有少量的水;今保持温度 不变,将体积加倍,压强变为2atm,底部的水恰好消失,试问
不变,将体积加倍,压强变为2atm,底部的水恰好消失,试问 是多少?若保持温度
是多少?若保持温度 不变,体积增为最多体积的4倍,试问这时容器内的压强是多少?容器内水和空气的质量各是多少?设饱和水汽可看作是理想气体。
不变,体积增为最多体积的4倍,试问这时容器内的压强是多少?容器内水和空气的质量各是多少?设饱和水汽可看作是理想气体。
解:设初态、中态和末态中空气分压强分别为 ;初态、中态中的水汽均为温度
;初态、中态中的水汽均为温度 的饱和汽,设饱和水汽压为
的饱和汽,设饱和水汽压为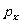 ;末态中的水汽为温度
;末态中的水汽为温度 的未饱和汽,水汽分压为
的未饱和汽,水汽分压为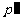 。若末态气体的压强为p,则有
。若末态气体的压强为p,则有
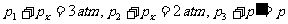
从初态变为中态的过程中,空气质量未变而水汽质量增加,对空气分压可用玻意尔定律

得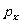 =1atm,故
=1atm,故 =373K,
=373K,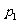 =2atm,
=2atm,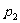 =1atm。从中态变为末态的过程,水汽和空气的总质量不变,应用玻意耳定律
=1atm。从中态变为末态的过程,水汽和空气的总质量不变,应用玻意耳定律

p=1atm
容器内空气的摩尔数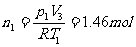 ,末态时空气和水汽的总摩尔数
,末态时空气和水汽的总摩尔数

故容器内水和水汽的总摩尔数
 。
。
例:由固态导热材料做成的长方体容器,被一隔板等分为两个互不连通的部分,其中分别贮有相等质量的干燥空气和潮湿空气,在潮湿空气中水汽质量占2%。
(1)若隔板可自由无摩擦地沿器壁滑动,试求达到平衡后干、湿空气所占体积的比值。
(2)若一开始采用能确保不漏气的方式将隔板抽出,试求达到平衡后容器内气体的压强与未抽出隔板时干、湿空气各自的压强这三者的比值(设干、湿空气均可视为理想气体)。
解:(1)隔板平衡的条件是:隔板两侧气体的压强相同,温度也相同(因容器和外界导热),所以对干空气有
 ①
①
而对潮湿空气有
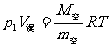

而


故得
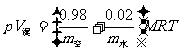 ②
②
得

(2)隔板抽出前,干湿空气的体积为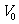 ,压强分别为
,压强分别为 ,则由克拉伯龙方程得
,则由克拉伯龙方程得
 ,
③
,
③
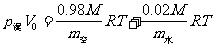 ,
④
,
④
抽出隔板以后,干、湿空气混合以后系统的压强为p,则
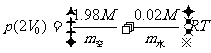 ⑤
⑤
故要求的三个压强之比为
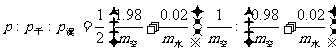
=1.006:1:1.012
说明湿空气在未达到饱和前遵循理想气体状态方程,当然克拉珀方程也适用,而在达到饱和以后,克拉珀龙方程仍可用,但理想气体状态方程则不适用了,因为水气的质量会发生变化。
4.2、1、液体的汽化
液体的汽化有蒸发和沸腾两种不同的形式。蒸发是发生在液体表面的汽化过程,在任何温度下都可以进行。沸腾是整个液体内部发生汽化过程,只在沸点下才能进行。
①蒸发
从微观上看,蒸发就是液体分子从液面跑出来的过程。分子从液面跑出来时,需要克服液体表面层中分子的引力做功,所以只有那些热运动动能较大的分子可以跑出来。如果不吸热,就会使液体中剩余分子的平均动能减小,温度降低。另一方面蒸气分子不断地返回到液体中去,凝结成液体。因此液体分子蒸发的数量,是液体分子跑出液面的数量,减少蒸气分子进入液面的数量。
对于液面敞开的情况,影响蒸发快慢的因素,主要有以下三种:一是液面的表面积,二是温度,三是液面上的通风情况。在液面敞开的情况下,液体会不断蒸发,直到液体全部转变为蒸起为止。
在密闭的容器中,随着蒸发的不断进行,容器内蒸汽的密度不断增大,这时返回液体中的蒸气分子数也不断增多,直到单位时间内跑出液面的分子数与反回液面的分子数相等时,宏观上看蒸发现象就停止了。这时液面上的蒸气与液体保持动态平衡,此时的蒸气叫做饱和蒸气,它的压强叫饱和蒸气压。
饱和气压与液体的种类有关,在相同的温度下,易蒸发的液体的饱和汽压大,不易蒸发的液体的饱和汽压小。对于同一种液体,饱和汽压随温度的升高而增大。饱和汽压的大小还与液面的形状有关,对于凹液面,分子逸出液面所需做的功比平液面时小。反之,对于凸液面,如小液滴或小气泡,才会显示出来。饱和汽压的数值与液面上蒸汽的体积无关,与该体积中有无其他气体无关。
在汽化过程中,体积增大,要吸收大量的热量。单位质量的液体完全变成同温度下的蒸汽所吸收的热量,叫做该物质在该温度下的汽化热。如100℃水的汽化热 。液体汽化时吸热,一方面用于改变系统的内能,同时也要克服外界压强作功。如果1mol液体和饱和汽的体积分别为
。液体汽化时吸热,一方面用于改变系统的内能,同时也要克服外界压强作功。如果1mol液体和饱和汽的体积分别为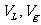 ,且
,且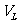 <<
<<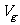 ,对饱和汽采用理想气体方程近似处理,
,对饱和汽采用理想气体方程近似处理,
②沸腾
液体内部和容器壁上存有小气泡,它能使液体能在其内部汽化,起着汽化核的作用。气泡内的总压强是泡内空气分压强 和液体的饱和汽压
和液体的饱和汽压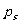 之和;气泡外的压强是液面上的外界压强
之和;气泡外的压强是液面上的外界压强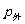 和
和 之和,通常情况下,液体静压强
之和,通常情况下,液体静压强 忽略不计。因此,在某一温度下,液内气泡的平衡条件为
忽略不计。因此,在某一温度下,液内气泡的平衡条件为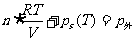 。当液体温度升高时,
。当液体温度升高时,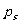 增大,同时由温度升高和汽化,体积膨胀,导致
增大,同时由温度升高和汽化,体积膨胀,导致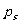 下降,这样在新的条件下实现与
下降,这样在新的条件下实现与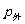 的平衡。当
的平衡。当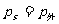 时,无论气泡怎样膨胀也不能实现平衡,处于非平衡状态。此时骤然长大的气泡,在浮力作用下,
时,无论气泡怎样膨胀也不能实现平衡,处于非平衡状态。此时骤然长大的气泡,在浮力作用下, 迅速上升到液面破裂后排出蒸气,整个液体剧烈汽化,这就是沸腾现象。相应的温度叫做沸点。对于同种液体,沸点与液面上的压强有关,压强越大,沸点越高。沸点还与液体的种类有关,在同一压强下,不同液体的沸点不同。
迅速上升到液面破裂后排出蒸气,整个液体剧烈汽化,这就是沸腾现象。相应的温度叫做沸点。对于同种液体,沸点与液面上的压强有关,压强越大,沸点越高。沸点还与液体的种类有关,在同一压强下,不同液体的沸点不同。
③双层液体沸腾的分析
在外界压强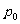 的条件下,若液体A的沸点77℃,液体B的沸点100℃。现将等质量的互不相容的液体A和B注入一个容器内,形成图4-2-1的双层液体。液体B的表面上再覆盖一薄层非挥发性的,与液体A、B互不相溶的液体C,目的是防止液体B上表面的
的条件下,若液体A的沸点77℃,液体B的沸点100℃。现将等质量的互不相容的液体A和B注入一个容器内,形成图4-2-1的双层液体。液体B的表面上再覆盖一薄层非挥发性的,与液体A、B互不相溶的液体C,目的是防止液体B上表面的
自由蒸发。现将此液体缓慢加热,它们的温度始终相等,液体温度随时间t变化关系为图示。
加热刚开始,对应图线左侧斜坡部分,液体B不能经上表面自由蒸发。下面考察系统内部的蒸发,设想在液体A或B内部,或在A、B分界面上各形成一个气泡,仅当泡内压强等于外界压强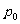 时,它才能保持上升而逸出此系统。液体A、B内部形成的气泡的内压强,分别等于A、B的饱和汽压,A、B交界面上形成气泡的内压强则为A、B的饱和汽压之和,因为这种气泡同时与A、B接触。因此加热时,液体交界面上形成气泡的压强首先达到
时,它才能保持上升而逸出此系统。液体A、B内部形成的气泡的内压强,分别等于A、B的饱和汽压,A、B交界面上形成气泡的内压强则为A、B的饱和汽压之和,因为这种气泡同时与A、B接触。因此加热时,液体交界面上形成气泡的压强首先达到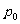 温度
温度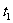 正是对应这种液体在相互接触区域发生的共同沸腾。
正是对应这种液体在相互接触区域发生的共同沸腾。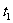 低于A、B各自的沸点,如
低于A、B各自的沸点,如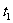 =67℃。当A、B中的一个全部蒸发后,系统的温度便会再次上升,对应图线的第二斜坡。温度
=67℃。当A、B中的一个全部蒸发后,系统的温度便会再次上升,对应图线的第二斜坡。温度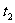 即为容器中余留液体的沸点。
即为容器中余留液体的沸点。
谁先全部蒸发呢?这取决于温度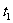 时,液体A、B在每个升高气泡中饱和蒸气的质量比,即
时,液体A、B在每个升高气泡中饱和蒸气的质量比,即 ,式中
,式中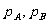 为温度
为温度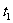 时A、B的饱和气压。如果
时A、B的饱和气压。如果 ,则A先全部蒸发,余留液体B,
,则A先全部蒸发,余留液体B,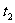 =100℃.
=100℃.
2.3.4、热力学第二定律的统计意义
对于热量传递,我们知道,高温物体分子的平均动能比低温物体分子的平均动能要大,两物体相接触时,能量从高温物体传到低温物体的概率显然比反向传递的概率大得多。对于热功转换,功转化为热是在外力作用下宏观物体的有规则定向运动转变为分子无规则运动的过程,这种转换的概率大,反之,热转化为功则是分子的无规则运动转变为宏观物体的有规则运动的过程,这种转化的概率小。所以,热力学第二定律在本质上是一条统计性的规律。一般说来,一个不受外界影响的封闭系统,其内部发生的过程,总是由概率小的状态向概率大的状态进行,由包含微观状态数目少的宏观状态向包含微观状态数目多的宏观状态进行,这是热力学第二定律统计意义之所在。
例1、某空调器按可逆卡诺循环运转,其中的作功装置连续工作时所提供的功率 。(1)夏天室外温度恒为
。(1)夏天室外温度恒为 ,启动空调器连续工作,最后可将室温降至恒定的
,启动空调器连续工作,最后可将室温降至恒定的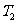 。室外通过热传导在单位时间内向室内传输的热量正比于(
。室外通过热传导在单位时间内向室内传输的热量正比于(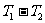 )(牛顿冷切定律),比例系数A。试用
)(牛顿冷切定律),比例系数A。试用 ,
, 和A来表示
和A来表示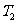 (2)当室外温度为30℃时,若这台空调只有30%的时间处于工作状态,室温可维持在20℃。试问室外温度最高为多少时,用此空调器仍可使室温维持在20℃。(3)冬天,可将空调器吸热、放热反向。试问室外温度最低为多少时,用此空调器可使室温维持在20℃。
(2)当室外温度为30℃时,若这台空调只有30%的时间处于工作状态,室温可维持在20℃。试问室外温度最高为多少时,用此空调器仍可使室温维持在20℃。(3)冬天,可将空调器吸热、放热反向。试问室外温度最低为多少时,用此空调器可使室温维持在20℃。
分析:夏天,空调机为制冷机,作逆向卡诺循环,从室内吸热,向室外放热,对工作物质作功。为保持室温恒定,空调器从室内吸热等于室外向室内通过热传导传输的热量。冬天刚好相反,空调器为热机,作顺向卡诺循环,从室外吸热,向室内放热。为保持室温恒定,空调器向室内的放热应等于室内向室外通过热传导传输的热量。
解:(1)夏天,空调器为制冷机,单位时间从室内吸热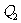 ,向室外放热
,向室外放热 ,空调器的平均功率为P,则
,空调器的平均功率为P,则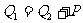 。对可逆卡诺循环,则有
。对可逆卡诺循环,则有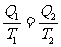 ,
,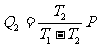 。通过热传导传热
。通过热传导传热 ,由
,由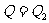 得
得


因空调器连续工作,式中 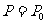 ,
, 
(2)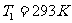 ,
, ,
,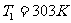 ,而所求的是
,而所求的是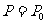 时对应的
时对应的 值,记为
值,记为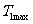 ,则
,则

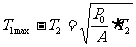
解得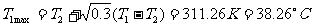 。
。
(3)冬天,空调器为热机,单位时间从室外吸热 ,向室内放热
,向室内放热 ,空调器连续工作,功率为
,空调器连续工作,功率为 ,有
,有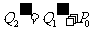 ,
, ,由热平衡方程得:
,由热平衡方程得:
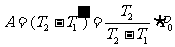
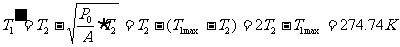
=
若空调器连续工作,则当冬天室外温度最低为1.74℃,仍可使室内维持在20℃。
2.3.3、卡诺定理
设有一过程,使物体从状态A变到状态B。对它来说,如果存在另一过程,它不仅使物体进行反向变化,从状态B回复到状态A,而且当物体回复到状态A时,周围一切也都各自回复到原状,则从状态A进行到状态B的过程是个可逆过程。反之,如对于某一过程,不论经过怎样复杂曲折的方法都不能使物体和外界恢复到原来状态而不引起其他变化,则此过程就是不可逆过程。
气体迅速膨胀是不可逆过程。气缸中气体迅速膨胀时,活塞附近气体的压强小于气体内部的压强。设气体内部的压强为P,气体迅速膨胀-微小体积△V,则气体所作的功W,小于p△V。然后,将气体压回原来体积,活塞附近气体的压强不能小于气体内部的压强,外界所作的功 不能小于p△V。因此,迅速膨胀后,我们虽然可以将气体压缩,使它回到原来状态,但外界多作功
不能小于p△V。因此,迅速膨胀后,我们虽然可以将气体压缩,使它回到原来状态,但外界多作功 ;功将增加气体的内能,而后以热量形式释放。根据热力学第二定律,我们不能通过循环过程再将这部分热量全部变为功;所以气体迅速膨胀的过程是不可逆过程。只有当气体膨胀非常缓慢,活塞附近的压强非常接近于气体内部的压强p时,气体膨胀-微小体积△V所作的功恰好等于p△V,那么我们才能非常缓慢地对气体作功p△V,将气体压回原来体积。所以,只有非常缓慢的亦即平衡的膨胀过程,才是可逆的膨胀过程。同理,只有非常缓慢的亦即平衡的压缩过程,才是可逆的压缩过程。在热力学中,过程的可逆与否和系统所经历的中间状态是否平衡密切相关。实际的一切过程都是不可逆过程。
;功将增加气体的内能,而后以热量形式释放。根据热力学第二定律,我们不能通过循环过程再将这部分热量全部变为功;所以气体迅速膨胀的过程是不可逆过程。只有当气体膨胀非常缓慢,活塞附近的压强非常接近于气体内部的压强p时,气体膨胀-微小体积△V所作的功恰好等于p△V,那么我们才能非常缓慢地对气体作功p△V,将气体压回原来体积。所以,只有非常缓慢的亦即平衡的膨胀过程,才是可逆的膨胀过程。同理,只有非常缓慢的亦即平衡的压缩过程,才是可逆的压缩过程。在热力学中,过程的可逆与否和系统所经历的中间状态是否平衡密切相关。实际的一切过程都是不可逆过程。
卡诺循环中每个过程都是平衡过程,所以卡诺循环是理想的可逆循环卡诺定理指出:(1)在同样高温(温度为 )和低温(温度为
)和低温(温度为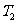 )之间工作的一切可逆机,不论用什么工作物,效率都等于
)之间工作的一切可逆机,不论用什么工作物,效率都等于 。(2)在同样高低温度热源之间工作的一切不可逆机的效率,不可能高于可逆机,即
。(2)在同样高低温度热源之间工作的一切不可逆机的效率,不可能高于可逆机,即
 ≤
≤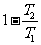 。
。
下面我们给予证明。
设高温热源 ,低温热源
,低温热源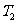 ,一卡诺理想可逆机E与另一可逆机
,一卡诺理想可逆机E与另一可逆机 ,在此两热源之间工作,设法调节使两热机可作相等的功W。现使两机结合,由可逆机
,在此两热源之间工作,设法调节使两热机可作相等的功W。现使两机结合,由可逆机 从高温热源吸热
从高温热源吸热 向低温热源放热
向低温热源放热 ,其效率
,其效率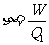 。可逆机
。可逆机 所作功W恰好提供给卡诺机E,而使E逆向进行,从低温热源吸热
所作功W恰好提供给卡诺机E,而使E逆向进行,从低温热源吸热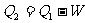 ,向高温热源放热
,向高温热源放热 ,其效率为
,其效率为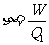 。我们用反证法,先设
。我们用反证法,先设 >
> 。由此得
。由此得 <
< ,即
,即 <
<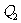 。当两机一起运行时,视他们为一部复合机,结果成为外界没有对这复合机作功,而复合机却能将热量
。当两机一起运行时,视他们为一部复合机,结果成为外界没有对这复合机作功,而复合机却能将热量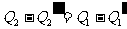 从低温热源送至高温热源,违反了热力学第二定律。所以
从低温热源送至高温热源,违反了热力学第二定律。所以 >
> 不可能。反之,使卡诺机E正向运行,而使可逆机
不可能。反之,使卡诺机E正向运行,而使可逆机 逆行运行,则又可证明
逆行运行,则又可证明 >
> 为不可能,即只有
为不可能,即只有 =
= 才成立,也就是说在相同的
才成立,也就是说在相同的 和
和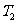 两温度的高低温热源间工作的一切可逆机,其效率均为
两温度的高低温热源间工作的一切可逆机,其效率均为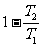 。
。
如果用一台不可逆机 来代替上面所说的
来代替上面所说的 。按同样方法可以证明
。按同样方法可以证明 >
> 为不可能,即只有
为不可能,即只有 ≥
≥ 。由于
。由于 是不可逆机,因此无法证明
是不可逆机,因此无法证明 ≤
≤ 。所以结论是
。所以结论是 ≥
≥ ,即在相同
,即在相同 和
和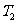 的两温度的高低温热源间工作的不可逆机,它的效率不可能大于可逆机的效率。
的两温度的高低温热源间工作的不可逆机,它的效率不可能大于可逆机的效率。
2.3.2、热力学第二定律
表述1:不可能制成一种循环动作的热机,只从一个热源吸取热量,使之全部变为有用的功,而其他物体不发生任何变化。
表述2:热量不可能自动地从低温物体转向高温物体。
在表述1中,我们要特别注意“循环动作”几个字,如果工作物进行的不是循环过程,如气体作等温膨胀,那么气体只使一个热源冷却作功而不放出热量便是可能的。该叙述反映了热功转换的一种特殊规律,并且表述1与表述2具有等价性。我们用反证法来证明两者的等价性。
 假设表述1不成立,亦即允许有一循环E可以从高温热源取得热量
假设表述1不成立,亦即允许有一循环E可以从高温热源取得热量 ,并全部转化为功W。这样我们再利用一个逆卡诺循环口接受E所作功W(=
,并全部转化为功W。这样我们再利用一个逆卡诺循环口接受E所作功W(= ),使它从低温热源
),使它从低温热源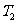 取得热量
取得热量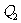 ,输出热量
,输出热量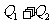 给高温热源。现在把这两个循环总的看成一部复合致冷机,其总的结果是,外界没有对他做功而它却把热量
给高温热源。现在把这两个循环总的看成一部复合致冷机,其总的结果是,外界没有对他做功而它却把热量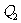 从低温热源传给了高温热源。这就说明,如果表述1不成立,则表述2也不成立。反之,也可以证明如果表述2不成立,则表述1也必然不成立。
从低温热源传给了高温热源。这就说明,如果表述1不成立,则表述2也不成立。反之,也可以证明如果表述2不成立,则表述1也必然不成立。
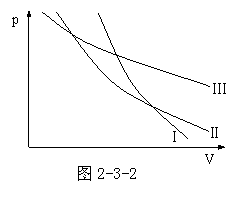
试证明在P-V图上两条绝热线不能相交。
假定两条绝热线Ⅰ与Ⅱ在P-V图上相交于一点A,如图2-3-2所示。现在,在图上再画一等温线Ⅲ,使它与两条绝热线组成一个循环。这个循环只有一个单热源,它把吸收的热量全部转变为功,即η=1,并使周围没有变化。显然,这是违反热力学第二定律的,因此两条绝热线不能相交。
2.3.1、卡诺循环
物质系统经历一系列的变化过程又回到初始状态,这样的周而复始的变化过程为循环过程,简称循环。在P-V图上,物质系统的循环过程用一个闭合的曲线表示。经历一个循环,回到初始状态时,内能不变。利用物质系统(称为工作物)持续不断地把热转换为功的装置叫做热机。在循环过程中,使工作物从膨胀作功以后的状态,再回到初始状态,周而复始进行下去,并且必而使工作物在返回初始状态的过程中,外界压缩工作物所作的功少于工作物在膨胀时对外所做的功,这样才能使工作物对外做功。获得低温装置的致冷机也是利用工作物的循环过程来工作的,不过它的运行方向与热机中工作物的循环过程相反。
 卡诺循环是在两个温度恒定的热源之间工作的循环过程。我们来讨论由平衡过程组成的卡诺循环,工作物与温度为
卡诺循环是在两个温度恒定的热源之间工作的循环过程。我们来讨论由平衡过程组成的卡诺循环,工作物与温度为 的高温热源接触是等温膨胀过程。同样,与温度为
的高温热源接触是等温膨胀过程。同样,与温度为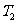 的低温热源接触而放热是等温压缩过程。因为工作物只与两个热源交换能量,所以当工作物脱离两热源时所进行的过程,必然是绝热的平衡过程。如图2-3-1所示,在理想气体卡诺循环的P-V图上,曲线ab和cd表示温度为
的低温热源接触而放热是等温压缩过程。因为工作物只与两个热源交换能量,所以当工作物脱离两热源时所进行的过程,必然是绝热的平衡过程。如图2-3-1所示,在理想气体卡诺循环的P-V图上,曲线ab和cd表示温度为 和
和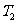 的两条等温线,曲线bc和da是两条绝热线。我们先讨论以状态a为始点,沿闭合曲线abcda所作的循环过程。在abc的膨胀过程中,气体对外做功
的两条等温线,曲线bc和da是两条绝热线。我们先讨论以状态a为始点,沿闭合曲线abcda所作的循环过程。在abc的膨胀过程中,气体对外做功 是曲线abc下面的面积,在cda的压缩过程中,外界对气体做功
是曲线abc下面的面积,在cda的压缩过程中,外界对气体做功 是曲线cda下面的面积。气体对外所做的净功
是曲线cda下面的面积。气体对外所做的净功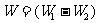 就是闭合曲线abcda所围面积,气体在等温膨胀过程ab中,从高温热源吸热
就是闭合曲线abcda所围面积,气体在等温膨胀过程ab中,从高温热源吸热 ,气体在等温压缩过程cd中,向低温热源放热
,气体在等温压缩过程cd中,向低温热源放热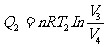 。应用绝热方程
。应用绝热方程  和
和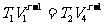 得
得 
所以
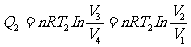
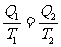
卡诺热机的效率
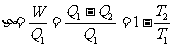
我们再讨论理想气体以状态a为始点,沿闭合曲线adcba所分的循环过程。显然,气体将从低温热源吸取热量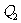 ,又接受外界对气体所作的功W,向高温热源传热
,又接受外界对气体所作的功W,向高温热源传热 。由于循环从低温热源吸热,可导致低热源的温度降得更快,这就是致冷机可以致冷的原理。致冷机的功效常用从低温热源中吸热
。由于循环从低温热源吸热,可导致低热源的温度降得更快,这就是致冷机可以致冷的原理。致冷机的功效常用从低温热源中吸热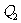 和所消耗的外功W的比值来量度,称为致冷系数,即
和所消耗的外功W的比值来量度,称为致冷系数,即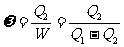 ,对卡诺致冷机而言,
,对卡诺致冷机而言, 。
。
有一卡诺致冷机,从温度为-10℃的冷藏室吸取热量,而向温度为20℃的物体放出热量。设该致冷机所耗功率为15kW,问每分钟从冷藏室吸取的热量是多少?
令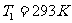 ,
, ,则
,则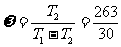 。每分钟作功
。每分钟作功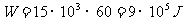 ,所以每分钟从冷藏室中吸热
,所以每分钟从冷藏室中吸热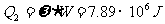 。
。
2.2.7、循环过程
系统由某一状态出发,经历一系列过程又回到原来状态的过程,称为循环过程。热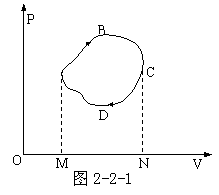 机循环过程在P-V图上是一根顺时针绕向的闭合曲线(如图2-2-1)。系统经过循环过程回到原来状态,因此△E=0。
机循环过程在P-V图上是一根顺时针绕向的闭合曲线(如图2-2-1)。系统经过循环过程回到原来状态,因此△E=0。
由图可见,在ABC过程中,系统对外界作正功,在CDA过程中,外界对系统作正功。在热机循环中,系统对外界所作的总功:
 (P-V图中循环曲线所包围的面积)而且由热力学第一定律可知:在整个循环中系统绕从外界吸收的热量总和
(P-V图中循环曲线所包围的面积)而且由热力学第一定律可知:在整个循环中系统绕从外界吸收的热量总和 ,必然大于放出的热量总和
,必然大于放出的热量总和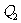 ,而且
,而且
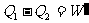
热机效率表示吸收来的热量有多少转化为有用的功,是热机性能的重要标志之一,效率的定义为

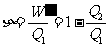 <1
<1
例1一台四冲程内燃机的压缩比r=9.5,热机抽出的空气和气体燃料的温度为
27℃,在larm= 压强下的体积为
压强下的体积为 ,如图2-2-2所示,从1→2是绝热压缩过程;2→3混合气体燃爆,压强加倍;从3→4活塞外推,气体绝热膨胀至体积
,如图2-2-2所示,从1→2是绝热压缩过程;2→3混合气体燃爆,压强加倍;从3→4活塞外推,气体绝热膨胀至体积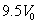 ;这是排气阀门打开,压强回到初始值larm(压缩比是气缸最大与最小体积比,γ是比热容比)。(1)确定状态1、2、3、4的压强和温度;(2)求此循环的热效率。
;这是排气阀门打开,压强回到初始值larm(压缩比是气缸最大与最小体积比,γ是比热容比)。(1)确定状态1、2、3、4的压强和温度;(2)求此循环的热效率。
分析:本题为实际热机的等容加热循环--奥托循环。其热效率取决于压缩比。
|
解:对于绝热过程,有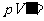 恒量,结合状态方程,有
恒量,结合状态方程,有 恒量。
恒量。
(1)状态1,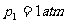 ,
,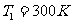

得
 ,
,
在状态3, ,
,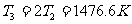
用绝热过程计算状态4,由 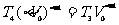
得
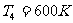 ,
, 。
。
(2)热效率公式中商的分母是2→3过程中的吸热,这热量是在这一过程中燃烧燃料所获得的。因为在这一过程中体积不变,不做功,所以吸收的热量等于气体内能的增加,即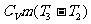 ,转化为功的有用能量是2→3过程吸热与4→1过程放热之差:
,转化为功的有用能量是2→3过程吸热与4→1过程放热之差:
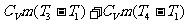
热效率为:

绝热过程有:  ,
,
因为 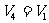 ,
,
故  ,
, , 而
, 而

因此
 。
。
热效率只依赖于压缩比,η=59.34%,实际效率只是上述结果的一半稍大些,因为大量的热量耗散了,没有参与循环。
§2-3 热力学第二定律
2.2.6、绝热过程的方程
绝热过程的状态方程是
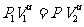 其中
其中 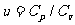
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com