
2、对于垂直入射,若k=0,呈现极大加强的波长为
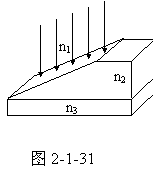

用以上的d值,得

对于任何厚度的膜层,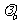 可从
可从 用同样的方式算出。在本题中
用同样的方式算出。在本题中

 它稍带黄色的绿光相对应。
它稍带黄色的绿光相对应。
例8、在半导体元件的生产中,为了测定Si片上的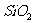 薄膜厚度,将
薄膜厚度,将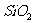 薄膜磨成劈尖形状。如图2-1-31所示,用波长λ=5461
薄膜磨成劈尖形状。如图2-1-31所示,用波长λ=5461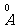 的绿光照射,已知
的绿光照射,已知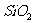 的折射率为1.46,Si的折射率了3.42,若观察到劈尖上出现了7个条纹间距,问
的折射率为1.46,Si的折射率了3.42,若观察到劈尖上出现了7个条纹间距,问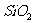 薄膜的厚度是多少?
薄膜的厚度是多少?
解:设图中从上到下依次为空气、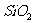 和Si,由于
和Si,由于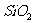 的折射率
的折射率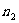 小于Si的折射率,所以光从空气射入
小于Si的折射率,所以光从空气射入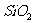 劈尖的上、下表面反射时都有半波损失,因此在棱边(劈膜厚度d=0处)为明条纹。当劈膜厚度d等于光在膜层中半波长的奇数倍时(或者膜层厚度d的2倍等于光在膜层中波长的整数倍时)都将出现明条纹。所以明条纹的位置应满足:
劈尖的上、下表面反射时都有半波损失,因此在棱边(劈膜厚度d=0处)为明条纹。当劈膜厚度d等于光在膜层中半波长的奇数倍时(或者膜层厚度d的2倍等于光在膜层中波长的整数倍时)都将出现明条纹。所以明条纹的位置应满足:
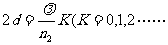
因此相邻明条纹对应的劈膜厚度差为

所以在劈膜开口处对应的膜层厚度为
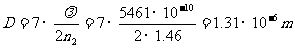
例9、利用劈尖状空气隙的薄膜干涉可以检测精密加工工件的表面质量,并能测量表面纹路的深度。测量的方法是:把待测工件放在测微显微镜的工作台上,使待测表面向上,在工件表面放一块具有标准光学平面的玻璃,使其光学平面向下,将一条细薄片垫在工件和玻璃板之间,形成劈尖状空气隙,如图2-1-32所示,用单色平行光垂直照射到玻璃板上,通过显微镜可以看到干涉条文。如果由于工件表面不平,观测中看到如图上部所示弯曲的干涉条纹。
①请根据条纹的弯曲方向,说明工件表面的纹路是凸起还不下凹?
②证明维路凸起的高度(或下凹的深度)可以表示为  ,
,
式中λ为入射单色光的波长,a、b的意义如图。
分析:在劈尖膜中讲过,空气隙厚度h与k存在相应关系。若工作表面十分平整,则一定观察到平行的干涉条纹。由于观察到的条纹向左弯曲,说明图中P点与Q点为同一k级明纹或暗纹。且某一k值与厚度h有线性正比关系。故P点与Q点对应的k相等,工件必下凹。
解①单色光在空气隙薄膜的上下表面反射,在厚度x满足:
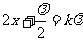
时出现明条纹,相邻明条纹所对应的空气隙的厚度差 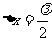 。
。
可见,对应于空气隙相等厚度的地方同是明条纹,或同是暗条纹。从图中可以看出,越向右方的条纹,所对应的空气隙厚度越大。故条纹左弯,工件必下凹。
②由图中看出,干涉条纹间距为b,对应的空气隙厚度差为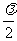 。又因为条纹最大弯曲程度为a,因此完所对应的纹路最大深度h应满足h:
。又因为条纹最大弯曲程度为a,因此完所对应的纹路最大深度h应满足h:
所以
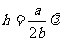 。
。
2、从垂直方向观察,薄膜是什么颜色?
肥皂膜液体的折射率n=1.33
解:1、入射到A点的光束一部分被反射,另一部分被折射并到达B点。在B点又有一部分再次被反射,并经折射后在C点出射。光线DC也在C点反射。远方的观察者将同时观察到这两条光线。
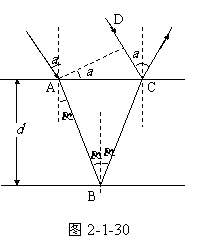 在平面AD上,整个光束有相同的相位。我们必须计算直接从第一表面来的光线与第二面来的光线之间的相位差。它取决于光程差,即取决于薄膜的厚度。无论发生干涉或相消干涉,白光中包含的各种波长的光线都会在观察的光中出现。
在平面AD上,整个光束有相同的相位。我们必须计算直接从第一表面来的光线与第二面来的光线之间的相位差。它取决于光程差,即取决于薄膜的厚度。无论发生干涉或相消干涉,白光中包含的各种波长的光线都会在观察的光中出现。
光线从A到C经第二表面反射的路程为


在媒质中波长为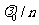 ,故在距离AB+BC上的波数为
,故在距离AB+BC上的波数为

光线从D到C经第一表面反射的路程为

在这段距离上,波长为 ,故波数为
,故波数为
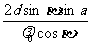
我们知道,当光从较大折射率的媒质反射时,光经历180。相位差,故DC段的波数为
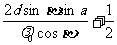
如果波数差为整数k,则出现加强,即
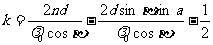


经过一些变换后,得到下述形式的加强条件
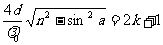
哪一种波长可得到极大加强,这只取决于几何路程和折射率。我们无法得到纯单色光。这是由于邻近波长的光也要出现,虽然较弱。k较大时,色彩就浅一些。所以如平板或膜太厚,就看不到彩色,呈现出一片灰白。本题中提到的绿光明亮,且要求薄膜的最小厚度。因此我们应取k=0,得到膜层厚度为
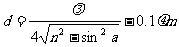
1、试问薄膜最小厚度为多少?
3.(1)如图2-1-29(a),点光源P移至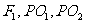 光线经过透镜后方向仍不变,而
光线经过透镜后方向仍不变,而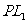 光线经上半透镜
光线经上半透镜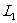 折射后变成与主轴平行的光线,
折射后变成与主轴平行的光线, 光线经下半透镜
光线经下半透镜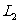 折射后与
折射后与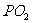 交于
交于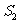 点,
点,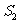 为P经下半透镜
为P经下半透镜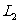 所成的实像点。
所成的实像点。
(2)图2-1-29 (a)中斜线所标出的范围为这种情况下的相干光束重叠区域。
 (3)这种情况在观察屏B上呈现出的干涉条纹也是以主轴为中心的一簇明暗相间的同心半圆环,但位于主轴上方,如图2-1-29(b)所示。
(3)这种情况在观察屏B上呈现出的干涉条纹也是以主轴为中心的一簇明暗相间的同心半圆环,但位于主轴上方,如图2-1-29(b)所示。
例7、一束白光以 °角射在肥皂膜上,反射光中波长
°角射在肥皂膜上,反射光中波长 的绿光显得特别明亮。
的绿光显得特别明亮。
2.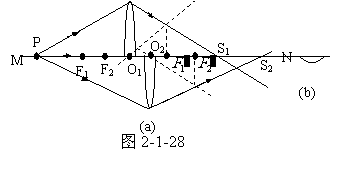 (1)如图2-1-28 (a),从点光源P引
(1)如图2-1-28 (a),从点光源P引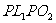 和
和 三条光线,
三条光线,
 过光心
过光心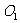 和
和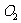 沿直线方向传播,过
沿直线方向传播,过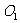 引平行于
引平行于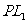 的辅助光线经
的辅助光线经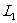 不发生折射沿原方向传播,与过
不发生折射沿原方向传播,与过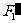 的焦面交于
的焦面交于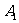 点,连接
点,连接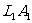 直线与主轴交于
直线与主轴交于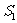 点,该点为P经上半透镜
点,该点为P经上半透镜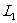 成像所得的实像点;同理可得P经下半透镜
成像所得的实像点;同理可得P经下半透镜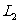 所成的实像点
所成的实像点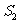 ,此二实像点沿主轴方向移开。
,此二实像点沿主轴方向移开。
(2)图2-1-28 (a)中斜线标出的范围为二相干光束交叠区。
(3)在观察屏B上的干涉条纹为以主轴为中心的一簇明暗相间的同心半圆环,位于主轴下方,如图2-1-28(b)所示。
3.在本题第2问的情况下,使点光源P沿主轴移到半透镜的焦点处,如图2-1-26所示,试回答第2问中各问。
解:1.(1)如图2-1-27,从点光源P引 和
和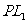 两条光线,
两条光线, 过
过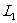 光心
光心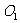 后沿原方向传播。引PO轴助光线,该光线与
后沿原方向传播。引PO轴助光线,该光线与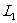 的主轴平行,若经
的主轴平行,若经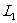 折射后必通过焦点
折射后必通过焦点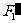 ,沿
,沿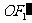 方向传播,与
方向传播,与 相交于
相交于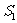 点,
点,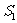 为P经上半透镜
为P经上半透镜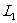 成像得到的实像点。同理,
成像得到的实像点。同理, 是P经下半透镜
是P经下半透镜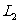 所成的实像点,连接
所成的实像点,连接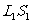 和
和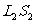 ,所得P点发出的光束经两半透镜折射后的光束的范围。
,所得P点发出的光束经两半透镜折射后的光束的范围。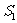 和
和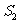 是二相干的实的点光源,像线所标的范围为相干光束交叠区。
是二相干的实的点光源,像线所标的范围为相干光束交叠区。
(2)在交叠区放一竖直的接收屏,屏上呈现出与纸面垂直的明暗相间的条纹,其条纹间距为

(3)屏B向右移动时,D增大,条纹间距增大。
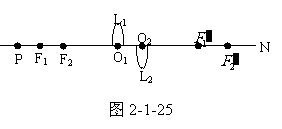
2. 将切开的二半透镜沿主轴MN方向移开一小段距离,构成干涉装置,如图2-1-25所示,P为单色光源,位于半透镜
将切开的二半透镜沿主轴MN方向移开一小段距离,构成干涉装置,如图2-1-25所示,P为单色光源,位于半透镜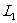 的焦点
的焦点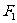 外。
外。
(1)用作图法画出干涉光路图。
 (2)用斜学标出相干光束交叠区。
(2)用斜学标出相干光束交叠区。
(3)在交叠区内放一观察屏,该屏与MN垂直,画出所呈现的干涉条纹的形状。
1. 将切开的二半透镜各沿垂直剖面的方向拉开,使剖面与MN的距离均为0.1mm,移开后的空隙用不透光的物质填充组成干涉装置,如图2-1-24所示,其中P点为单色点光源
将切开的二半透镜各沿垂直剖面的方向拉开,使剖面与MN的距离均为0.1mm,移开后的空隙用不透光的物质填充组成干涉装置,如图2-1-24所示,其中P点为单色点光源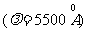 ,PO=20cm,B为垂直于MN的屏,OB=40cm。
,PO=20cm,B为垂直于MN的屏,OB=40cm。
(1)用作图法画出干涉光路图。
(2)算出屏B上呈现的干涉条纹的间距。
(3)如屏B向右移动,干涉条纹的间距将怎样变化?
2、由以上的求解过程可知,干涉条纹间距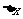 与屏幕离透镜L的距离无关,这正是两束平行光干涉的特点。但屏幕必须位于两束光的相干叠加区才行。图2-1-22中以阴影菱形部分表示这一相干叠加区。因为由(1)式知条纹是等距的,显然当屏幕位于PQ处可获得最多的干涉条纹,而PQ平面到
与屏幕离透镜L的距离无关,这正是两束平行光干涉的特点。但屏幕必须位于两束光的相干叠加区才行。图2-1-22中以阴影菱形部分表示这一相干叠加区。因为由(1)式知条纹是等距的,显然当屏幕位于PQ处可获得最多的干涉条纹,而PQ平面到 透镜L的距离
透镜L的距离

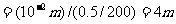
 例6.如图2-1-23所示,薄透镜的焦距f=10cm,其光心为O,主轴为MN,现将特镜对半切开,剖面通过主轴并与纸面垂直。
例6.如图2-1-23所示,薄透镜的焦距f=10cm,其光心为O,主轴为MN,现将特镜对半切开,剖面通过主轴并与纸面垂直。
2. 为获得最多的干涉条纹,屏幕应离透镜多远?
为获得最多的干涉条纹,屏幕应离透镜多远?
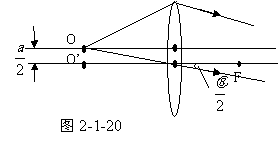
解:1、首先讨论粘合透镜的上半个透镜的成像。在图2-1-20中OO是
粘合透镜的中心轴线,在OO上方用实线画出了上半个透镜,在OO下方未画下半个透镜,而是补足了未切割前整个透镜的其余部分,用虚线表示。整个透镜的光轴为 .
.
半个透镜产成像规律应与完整的透像相同。现在物点(即光源)S在粘合透镜的中心轴线上,即在图中透镜的光轴上方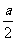 处,离透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜折射后成为一束平行光束,其传播方向稍偏向下方,与光轴
处,离透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜光心的水平距离正好是透镜的焦距。根据几何光学,光源S发出的光线,经透镜折射后成为一束平行光束,其传播方向稍偏向下方,与光轴 (对OO也是一样)成角为
(对OO也是一样)成角为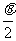
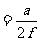 。当透镜完整时光束的宽度为:透镜直径
。当透镜完整时光束的宽度为:透镜直径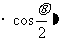 透镜直径。对于上半个透就,光事宽度为
透镜直径。对于上半个透就,光事宽度为 。
。
 同理,S所发的光,经下半个透镜折射后,形成稍偏向上方的平行光束,与
同理,S所发的光,经下半个透镜折射后,形成稍偏向上方的平行光束,与 轴成
轴成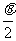 角,宽度也是
角,宽度也是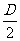 。
。
于是,在透镜右侧,成为夹角为θ的两束平行光束的干涉问题(见图2-1-21),图中的两平行光束的重叠区(用阴影表示)即为干涉区。为作图清楚起见,图2-1-21,特别是图12-1-21中的θ角,均远较实际角度为大。
 图2-1-22表示的是两束平行光的干涉情况,其中θ是和图2-1-21中的θ相对应的。图2-1-22中实线和虚线分别表示某一时刻的波峰平面和波谷平面。在垂直于中心轴线屏幕上,A、B、C表示相长干涉的亮纹位置,D、E表示相消干涉的暗纹位置,相邻波峰平面之间的垂直距离是波长λ。故干涉条纹间距△x满足
图2-1-22表示的是两束平行光的干涉情况,其中θ是和图2-1-21中的θ相对应的。图2-1-22中实线和虚线分别表示某一时刻的波峰平面和波谷平面。在垂直于中心轴线屏幕上,A、B、C表示相长干涉的亮纹位置,D、E表示相消干涉的暗纹位置,相邻波峰平面之间的垂直距离是波长λ。故干涉条纹间距△x满足

在θ很小的情况下,上式成为 。
。
所以透镜切去的宽度
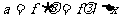
=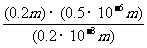


果然是一个很小的角度。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com