
2.2.4、光压
光压就是光子流产生的压强,从光子观点看,光压产生是由于光子把它的动量传给物体的结果
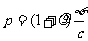
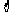 为入射光强,
为入射光强,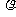 为壁反射系数。
为壁反射系数。
2.2.3、康普顿效应
当用可见光或紫外线作为光电效应的光源时,入射的光子将全部被电子吸收。但如果用X射线照射物质,由于它的频率高,能量大,不会被电子全部吸收,只需交出部分能量,就可以打出光电子,光子本身频率降低,波长变长。这种光电效应现象称为康普顿效应。
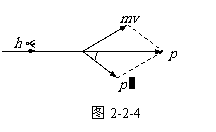 当X射线光子与静止的电子发生碰撞时,可以用p表示入射光子的动量,代表散射光子的动量,
当X射线光子与静止的电子发生碰撞时,可以用p表示入射光子的动量,代表散射光子的动量,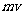 代表光电子的动量。则依据动量守恒定律,可以用图2-2-4表示三者的矢量关系。由于
代表光电子的动量。则依据动量守恒定律,可以用图2-2-4表示三者的矢量关系。由于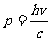 ,所以
,所以
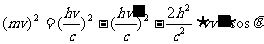
由能量守恒定律得出:
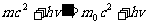
式中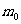 表示电们的静止质量,
表示电们的静止质量,
m表示运动电子的质量,有图2-4

联立上述各式,并将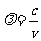 代入整理得
代入整理得

2.2.2、光子说
光电效应的四个特点中,只有第四个特点够用电磁来解释,其他特点都与电磁场理论推出的结果相矛盾。爱因斯坦于1905年提出的光子说,完美地解释了这一现象。
光子说指出:空间传播的光(以及其他电磁波)都是不连续的,是一份一份的,每一份叫做一个光子。光子的能量跟它的频率成正比即
E=hv
式中h为普朗克恒量。光子也是物质,它具有质量,其质量等于
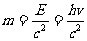
光子也具有动量,其动量等于
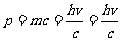
根据能量守恒定律得出:
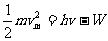
上式称为爱因斯坦光电效应方程。式中W称为材料的逸出功,表示电子从物而中逸出所需要的最小能量。某种物质产生光电效应的极限频率就由逸出功决定:
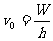
不同物质电子的逸出功不同,所对应的极限频率也不同。
在图2-3中,图线与v轴的交点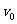 为极限频率,将图线反身延长与
为极限频率,将图线反身延长与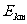 轴的交点对应的数值的绝对值就是W。图线的斜率表示普朗克恒量的数值,因此,图示电路还可以用来测定普朗克恒量。
轴的交点对应的数值的绝对值就是W。图线的斜率表示普朗克恒量的数值,因此,图示电路还可以用来测定普朗克恒量。
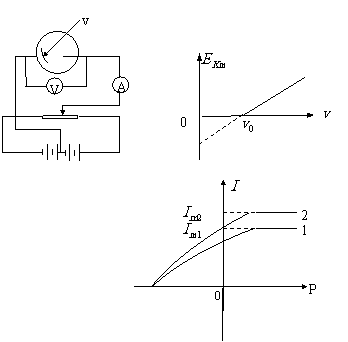
2.2.1、光电效应
某些物质在光(包括不可见光)的照射下有电子发射出来,这就是光电效应的现象。利用容易产生光电效应的物质制成阴极的电子管称为光电管。
图2-2-1所示的电来研究光电效应的规律。实验发现了光电效应的如下规律:
光电效应过程非常快,从光照到产生光电子不超过 ,停止光照,光电效应也立即停止。
,停止光照,光电效应也立即停止。
各种材料都有一个产生光电效应的极限频率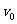 。入射光的效率必须高于
。入射光的效率必须高于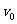 才能产生光电效应;频率低于
才能产生光电效应;频率低于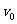 的入射光,无论其强度多大,照射时间多长,都不能产生光电效应。不同的物质,一般极限频率都不同。
的入射光,无论其强度多大,照射时间多长,都不能产生光电效应。不同的物质,一般极限频率都不同。
逸出的光电子的最大初动能可以这样测定,将滑动变阻器的滑片逐渐向左移动,直到光电流截止,读出这时伏特表的读数即为截止电压U。根据动能定理,光电子克服反向电压作的功等于动能的减小,即
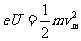
实验结果表明,当入射光频率一定时,无论怎样改变入射光的强度,截止电压都不会改变;入射光频率增大,截止电压也随着呈线性增大。这说明,逸出的光电子的
最大初动能只能随入射光频率增大而增大,与入射光强度无关。最大初动能与入射光频率的关系如图2-2-1所示。
在入射光频率一定条件下,向右移动变阻器的滑动片,光电流的强度随着逐渐增大,但当正向电压增大到某一值后继续再增大时,光电流维持一个固定图2-3值不变,此时光电流达到饱和。增大入射光的强度P,饱和光电流也随着成正比地增大。如图2-2-1所示。
2.1.4、光的偏振
光波是横波,这可以用光的偏振实验来证明。
通过两块偏振片来观察某一普通发光源,旋转其中一块偏振片,我们会发现,每旋转360。,观察到的光强会由暗变亮再变暗再变亮的交替变化两次,下面来解释这一现象。
 普通光源是为数众多的分子或原子在发光,虽然每一个原子发出的光只有一个特定的振动方向,但众多的原子发出光振动方向是杂乱的,没有哪一个方向比其他方向更特殊,这种光称为自然光。而偏振片具有让一个方向的振动通过(称为透光方向),另一个垂直方向的振动具有全部吸收的功能。这样,自然光通过偏振片后,只有一个方向振动的及其他方向振动在该方向的分量通过从而形成只有一个振动方向的线偏振光。当该线偏振光通过第二偏振片时,若第二偏振片的透光方向与线偏振方向(第一偏振片的透光方向)成α角,透过第二偏振片的振动时为
普通光源是为数众多的分子或原子在发光,虽然每一个原子发出的光只有一个特定的振动方向,但众多的原子发出光振动方向是杂乱的,没有哪一个方向比其他方向更特殊,这种光称为自然光。而偏振片具有让一个方向的振动通过(称为透光方向),另一个垂直方向的振动具有全部吸收的功能。这样,自然光通过偏振片后,只有一个方向振动的及其他方向振动在该方向的分量通过从而形成只有一个振动方向的线偏振光。当该线偏振光通过第二偏振片时,若第二偏振片的透光方向与线偏振方向(第一偏振片的透光方向)成α角,透过第二偏振片的振动时为 ,其光强为
,其光强为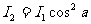 ,当α=90。、270。时,
,当α=90。、270。时,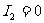 ;当α为0。、180。时,
;当α为0。、180。时,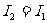 最大;其他角度在两者之间变化。这种偏振现象只有横波才有。
最大;其他角度在两者之间变化。这种偏振现象只有横波才有。
§2.2、 光的量子性
4、衍射光栅
由大量等宽度等间距的平行狭缝所组成的光学元件称为衍射光栅,将衍射光栅放置在图2-1-35的狭缝位置上,在衍射屏上便可观察到瑞利的亮条纹,这些亮条纹所对应的角度θ应满足

d为两狭缝之间的间距,m称为衍射级数。上式称为光栅方程。从方程中可以看出。不同的波长λ,其亮条纹所对应的θ不同,所以光栅可以用来作光谱仪器的色散元件。
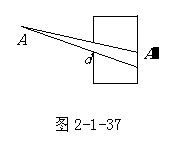 例1、一个由暗盒组成的针孔照相机,其小孔直径为d,暗盒中像成在小孔后距离为D的感光胶片上如图2-1-37,物体位于小孔前L处,所用波长为λ。(1)估计成像清晰时小孔半径的大小。(2)若使用中算出的小孔,试问物体上两点之间的最小距离是多少时?该两点的像是否可分辨?
例1、一个由暗盒组成的针孔照相机,其小孔直径为d,暗盒中像成在小孔后距离为D的感光胶片上如图2-1-37,物体位于小孔前L处,所用波长为λ。(1)估计成像清晰时小孔半径的大小。(2)若使用中算出的小孔,试问物体上两点之间的最小距离是多少时?该两点的像是否可分辨?
解:(1)物体上一点在照像底片上成的像由两个因素决定的,一是小孔的几何投影,一是小孔的夫琅禾费衍射(D»d)。几何投影产生物点的像的直径是
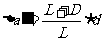
衍射效应扩大了几何投影区,所增加的直径大小为
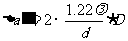
总的像直径为
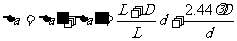
可见当小孔d小时,则第一项小,第二项大。当d大时,第二项小,第一项大。
当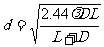 时,
时, 最小,其值是
最小,其值是

(2)由(1)知,对小孔直径为d的针孔照像机,物上一几何点在底片上所成像的大小为
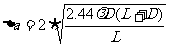
物上相邻两点AB在底片上要能分辨,根据瑞利判据,其像点中心距离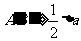 ,由几何关系得
,由几何关系得

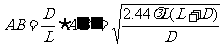
即物上两点间的距离要大于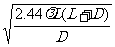 时,该两点的像是能分辨的。
时,该两点的像是能分辨的。
例2、用分波带矢量作图方法求出单缝的夫琅禾费衍射分布。
 解: 将缝宽为b的狭缝分成N条宽度相等的极窄条,称为子缝,其宽为
解: 将缝宽为b的狭缝分成N条宽度相等的极窄条,称为子缝,其宽为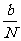 , N很大,则每一子缝可作为一几何线,这些子缝到屏上某一点P的距离想差很小,所以它们在P点引起的振幅a近似相等。至于位相,每一条子缝到P点是不同的,但相邻两子缝在屏上所引起的位相差为
, N很大,则每一子缝可作为一几何线,这些子缝到屏上某一点P的距离想差很小,所以它们在P点引起的振幅a近似相等。至于位相,每一条子缝到P点是不同的,但相邻两子缝在屏上所引起的位相差为 为如图2-1-38(b)所示的光程差,它等于
为如图2-1-38(b)所示的光程差,它等于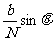 ,第一条子缝与最后一条子缝总位相差
,第一条子缝与最后一条子缝总位相差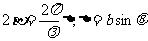 ,见图2-1-38(a)。各子缝在P点产生的振动E;叠加即为整个缝在P点的振动
,见图2-1-38(a)。各子缝在P点产生的振动E;叠加即为整个缝在P点的振动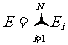 。这振动叠加可借助其矢量作图法来求出,如图2-1-39为矢量量,图中矢量图,图中矢量总长度是相同的,都为Na.
。这振动叠加可借助其矢量作图法来求出,如图2-1-39为矢量量,图中矢量图,图中矢量总长度是相同的,都为Na.
当β=0,即θ=0对应的中心点上,缝上各点波面到达时振动位相同,则各点振幅矢量合成如图2-1-39(a)。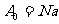 代表此点的合振动,这时光强最大(即主最大).对任一β,缝上相邻各点的振动位相相差
代表此点的合振动,这时光强最大(即主最大).对任一β,缝上相邻各点的振动位相相差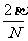 ,对应的矢量将转动
,对应的矢量将转动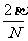 ,缝上两边缘的位相差为2β,各矢量构成一圆心角为2β的弧如图(b),它们的合矢量A等于这段弧的弦。由几何关系可得
,缝上两边缘的位相差为2β,各矢量构成一圆心角为2β的弧如图(b),它们的合矢量A等于这段弧的弦。由几何关系可得
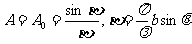
其强度
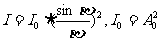
当β=π,即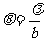 时,振幅矢量卷成一圆,故A=0,如图(c)。随着β增大,即θ增大,矢量曲线将越卷越小,合矢量也越来越小,对应的强度也随之减小。
时,振幅矢量卷成一圆,故A=0,如图(c)。随着β增大,即θ增大,矢量曲线将越卷越小,合矢量也越来越小,对应的强度也随之减小。
3、单缝和圆孔的夫琅和费衍射
夫琅和费衍射又称远场衍射,使用的是平行光线,即可认为光源距离为无限远。它不同于光源距离有限的菲涅耳衍射。在实验装置中更有价值。
夫琅和费衍射指用平行光照射障碍物时在无穷远处的衍射图像。由于无穷远与透镜的焦平面上是一对共扼面,所以可以用透镜将无穷远处的衍射花样成像于焦平面上
单缝的夫琅和费衍射装置如图2-1-35所示,S为与狭缝平行的线光源,置于 的前半焦平面上,由惠更斯-菲涅耳原理可计算出屏上任一点P的光强为
的前半焦平面上,由惠更斯-菲涅耳原理可计算出屏上任一点P的光强为
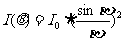
 式中,
式中,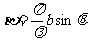 ,λ为波长,b为狭缝宽度,θ为P点对
,λ为波长,b为狭缝宽度,θ为P点对 中心轴线所张的角,
中心轴线所张的角,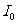 为中心点光强。
为中心点光强。
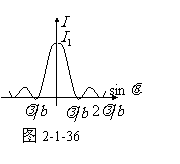
单缝的夫琅和费衍射图像和光强分布如图2-1-36,在衍射光强分布中,可知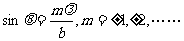 时,I=0。其中心条纹对应的夹角为
时,I=0。其中心条纹对应的夹角为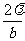 ,屏上的宽度则为
,屏上的宽度则为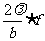 (f为
(f为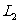 的焦距)。它表明,当狭缝官宽b变小时,中心衍射条纹变宽。
的焦距)。它表明,当狭缝官宽b变小时,中心衍射条纹变宽。
若用点光源和圆孔分别代替图2-1-35中的线光源S和狭缝,在屏便可得到小圆孔的衍射花样,
其光强分布如图2-1-37.D为小圆孔的直径,中央亮圆斑称为爱里斑,爱里斑边缘对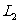 中心光轴的夹角为
中心光轴的夹角为 。
。
圆孔衍射是非常重要的,在光学仪强中,光学元件的边缘一般就是圆孔,对于一物点,由于这元件边缘的衍射,所成的像不再是点,而是一个爱里斑,这将影响光学仪器的分辩相邻物点的能力。根据瑞利判据,当两个爱里斑中心角距离为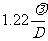 时,这两个像点刚好可以分辩,小于
时,这两个像点刚好可以分辩,小于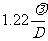 就不可分辨了。
就不可分辨了。
2、圆孔与圆屏的菲涅耳衍射
(1)圆孔衍射
 将一束光(如激光)投射在一个小圆孔上,并在距孔1-2米处放置一玻璃屏,则在屏上可看到小圆孔的衍射花样。
将一束光(如激光)投射在一个小圆孔上,并在距孔1-2米处放置一玻璃屏,则在屏上可看到小圆孔的衍射花样。
其中波带改为
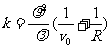
其中由圆孔半径P,光的波长λ,圆孔位置(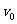 与R)确定。
与R)确定。
(2)圆屏衍射
不问圆屏大小和位置怎样,圆屏几何影子的中心永远有光,泊松亮斑即典型。
2.1.3 光的衍射
光绕过障碍物偏离直线传播而进入几何阴影,并在屏幕上出现光强不均匀分布的现象,叫做光的衍射。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com