
1.2.4、匀强电场中电势差与场强的关系
 场强大小和方向都相同的电场为匀强电场,两块带等量异种电荷的平板之间的电场可以认为是匀强电场,它的电场线特征是平行、等距的直线。
场强大小和方向都相同的电场为匀强电场,两块带等量异种电荷的平板之间的电场可以认为是匀强电场,它的电场线特征是平行、等距的直线。
场强与电势虽然都是反映场强本身性质特点的物理量,但两者之间没有相应的对应联系,但沿着场强方向电势必定降低,而电势阶低最快的方向也就是场强所指方向,在匀强电场中,场强E与电势差U之间满足
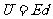
这就是说,在匀强电场中,两点间的电势等于场强大小和这两点在沿场强方向的位移的乘积。
例4、半径为R的半球形薄壳,其表面均匀分布面电荷密度为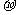 的电荷,求该球开口处圆面上任一点的电势。
的电荷,求该球开口处圆面上任一点的电势。
解: 设想填补面电荷密度亦为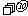 的另半个球面如图1-2-3所示,则球内任一点的场强均为0,对原半球面开口处圆面上的任一点P而言,也有
的另半个球面如图1-2-3所示,则球内任一点的场强均为0,对原半球面开口处圆面上的任一点P而言,也有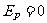 ,而
,而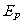 是上、下两个半球在P点产生场强
是上、下两个半球在P点产生场强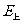 、
、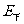 的合成。另据对称性易知,
的合成。另据对称性易知,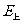 、
、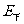 的大小必定相等,
的大小必定相等,
而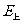 、
、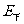 的合场强为零,说明
的合场强为零,说明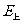 、
、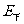 均垂直于半球开口平面,故在半球面带均匀电荷的情况下,它的开口圆面应为等势点,即圆面上任一点的电势都等于开口圆面圆心点处的电势。故
均垂直于半球开口平面,故在半球面带均匀电荷的情况下,它的开口圆面应为等势点,即圆面上任一点的电势都等于开口圆面圆心点处的电势。故
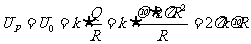
说明 虽然场强与电势是描述电场不同方面特性的两个物理量,它们之间没有必然的对应关系,但电势相等的各点构成的等势面应与该处的场强方向垂直,利用这个关系可为求取场强或电势提供一条有用的解题路径。
§1. 3、电场中的导体与电介质
一般的物体分为导体与电介质两类。导体中含有大量自由电子;而电介质中各个分子的正负电荷结合得比较紧密。处于束缚状态,几乎没有自由电荷,而只有束缚电子当它们处于电场中时,导体与电介质中的电子均会逆着原静电场方向偏移,由此产生的附加电场起着反抗原电场的作用,但由于它们内部电子的束缚程度不同。使它们处于电场中表现现不同的现象。
1.2.3、电势叠加原理
电势和场强一样,也可以叠加。因为电势是标量,因此在点电荷组形成的电场中,任一点的电势等于每个电荷单独存在时,在该点产生的电势的代数和,这就是电势叠加原理。
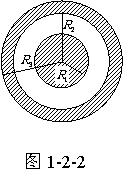
例3、如图1-2-2所示,两个同心导体球,内球半径为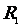 ,外球是个球壳,内半径为
,外球是个球壳,内半径为 ,外半径
,外半径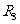 。在下列各种情况下求内外球壳的电势,以及壳内空腔和壳外空间的电势分布规律。
。在下列各种情况下求内外球壳的电势,以及壳内空腔和壳外空间的电势分布规律。
(1)内球带 ,外球壳带
,外球壳带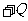 。
。
(2)内球带 ,外球壳不带电。
,外球壳不带电。
(3)内球带 ,外球壳不带电且接地。
,外球壳不带电且接地。
(4)内球通过外壳小孔接地,外球壳带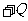 。
。
解: 如图1-2-2所示,根据叠原理:
(1)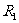 处有均匀的
处有均匀的 ,
, 必有均匀的
必有均匀的 ,
,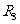 处当然有
处当然有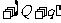 电荷,因此:
电荷,因此:
内球 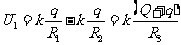
外球 
电势差 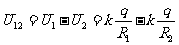
腔内 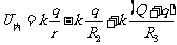 (
(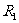 <r<
<r< )
)
壳外  (r>
(r>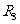 )
)
(2)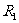 处有
处有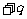 ,
, 处有
处有 ,
,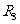 处有
处有 ,因此:
,因此:
内球 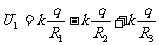
外球 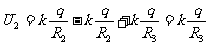
电势差 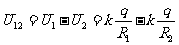
腔内  (
(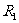 <r<
<r< )
)
壳外 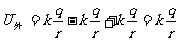 (r>
(r>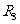 )
)
(3)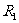 处有
处有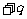 ,
, 处有
处有 ,外球壳接地,外球壳
,外球壳接地,外球壳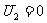 ,
,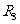 处无电荷。
处无电荷。
内球 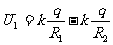
电势差 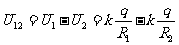
腔内 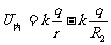 (
(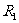 <r<
<r< )
)
壳外 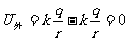 (r>
(r>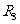 )
)
(4)内球接地电势为零,内球带 ,
, 处有
处有 ,
,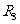 处有
处有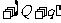 ,先求
,先求 ,因为
,因为 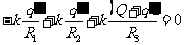
解得 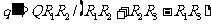
内球 
外球 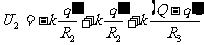
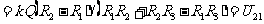
腔内 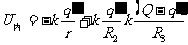
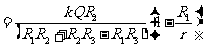 (
( <r<
<r< )
)
壳外 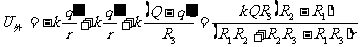
1.2.2、 几种常见带电体的电势分布
(1)点电荷周围的电势
如图1-2-1所示,场源电荷电量为Q,在离Q为r的P点处有一带电量为q的检验电荷, 现将该检验电荷由P点移至无穷远处(取无穷远处为零电势),由于此过程中,所受电场力为变力,故将q移动的整个过程理解为由P移至很近的
现将该检验电荷由P点移至无穷远处(取无穷远处为零电势),由于此过程中,所受电场力为变力,故将q移动的整个过程理解为由P移至很近的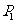 (离Q距离为
(离Q距离为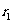 )点,再由
)点,再由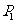 移至很近的
移至很近的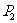 (离Q距离为
(离Q距离为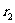 )点……直至无穷远处。在每一段很小的过程中,电场力可视作恒力,因此这一过程中,电场力做功可表示为:
)点……直至无穷远处。在每一段很小的过程中,电场力可视作恒力,因此这一过程中,电场力做功可表示为:
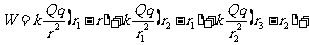 ……
……
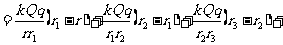 ……
……
 ……
……
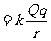
所以点电荷周围任一点的电势可表示为:
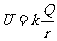
式中Q为场源电荷的电量,r为该点到场源电荷的距离。
(2)均匀带电球壳,实心导体球周围及内部的电势。
由于实心导体球处于静电平衡时,其净电荷只分布在导体球的外表面,因此其内部及周围电场、电势的分布与均匀带电球壳完全相同。由于均匀带电球壳外部电场的分布与点电荷周围电场的分布完全相同,因此用上面类似方法不难证明均匀带电球壳周围的电势为。
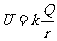 r>R
r>R
式中Q为均匀带电球壳的电量,R为球壳的半径,r为该点到球壳球心的距离。
在球壳上任取一个微元,设其电量为 ,该微元在球心O处产生的电势
,该微元在球心O处产生的电势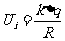 。由电势叠加原理,可知O点处电势等于球壳表面各微元产生电势的代数和,
。由电势叠加原理,可知O点处电势等于球壳表面各微元产生电势的代数和,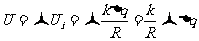 。
。
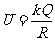
因为均匀带电球壳及实心导体球均为等势体,因而它们内部及表面的电势均为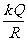 。
。

1.2.1、 电势差、电势、电势能
电场力与重力一样,都是保守力,即电场力做功与具体路径无关,只取决于始末位置。我们把在电场中的两点间移动电荷所做的功与被移动电荷电量的比值,定义为这两点间的电势差,即
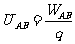
这就是说,在静电场内任意两点A和B间的电势差,在数值等于一个单位正电荷从A沿任一路径移到B的过程中,电场力所做的功。反映了电场力做功的能力。即电势差仅由电场本身性质决定,与被移动电荷的电量无关;即使不移动电荷,这两点间的电势差依然存在。
如果我们在电场中选定一个参考位置,规定它为零电势点,则电场中的某点跟参考位置间的电势差就叫做该点的电势。通常我们取大地或无穷远处为零电势点。电势是标准量,其正负代表电势的高低,单位是伏特(V)。
电势是反映电场能的性质的物理量,电场中任意一点A的电势,在数值上等于一个单位正电荷A点处所具有的电势能,因此电量为q的电荷放在电场中电势为U的某点所具有的电势能表示为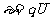 。
。
1.1.5、 电通量、高斯定理、
(1)磁通量是指穿过某一截面的磁感应线的总条数,其大小为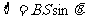 ,其中
,其中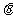 为截面与磁感线的夹角。与此相似,电通量是指穿过某一截面的电场线的条数,其大小为
为截面与磁感线的夹角。与此相似,电通量是指穿过某一截面的电场线的条数,其大小为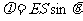
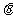 为截面与电场线的夹角。
为截面与电场线的夹角。
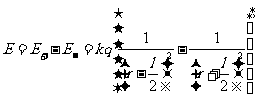
高斯定量:在任意场源所激发的电场中,对任一闭合曲面的总通量可以表示为
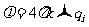 (
( )
) 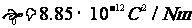 为真空介电常数
为真空介电常数
式中k是静电常量,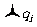 为闭合曲面所围的所有电荷电量的代数和。由于高中缺少高等数学知识,因此选取的高斯面即闭合曲面,往往和电场线垂直或平行,这样便于电通量的计算。尽管高中教学对高斯定律不作要求,但笔者认为简单了解高斯定律的内容,并利用高斯定律推导几种特殊电场,这对掌握几种特殊电场的分布是很有帮助的。
为闭合曲面所围的所有电荷电量的代数和。由于高中缺少高等数学知识,因此选取的高斯面即闭合曲面,往往和电场线垂直或平行,这样便于电通量的计算。尽管高中教学对高斯定律不作要求,但笔者认为简单了解高斯定律的内容,并利用高斯定律推导几种特殊电场,这对掌握几种特殊电场的分布是很有帮助的。
(2)利用高斯定理求几种常见带电体的场强
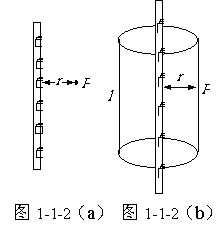
①无限长均匀带电直线的电场
一无限长直线均匀带电,电荷线密度为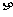 ,如图1-1-2(a)所示。考察点P到直线的距离为r。由于带电直线无限长且均匀带电,因此直线周围的电场在竖直方向分量为零,即径向分布,且关于直线对称。取以长直线为主轴,半径为r,长为l的圆柱面为高斯面,如图1-1-2(b),上下表面与电场平行,侧面与电场垂直,因此电通量
,如图1-1-2(a)所示。考察点P到直线的距离为r。由于带电直线无限长且均匀带电,因此直线周围的电场在竖直方向分量为零,即径向分布,且关于直线对称。取以长直线为主轴,半径为r,长为l的圆柱面为高斯面,如图1-1-2(b),上下表面与电场平行,侧面与电场垂直,因此电通量
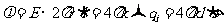
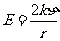
②无限大均匀带电平面的电场
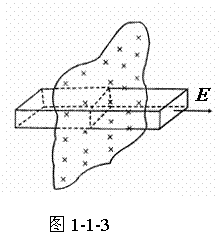
根据无限大均匀带电平面的对称性,可以判定整个带电平面上的电荷产生的电场的场强与带电平面垂直并指向两侧,在离平面等距离的各点场强应相等。因此可作一柱形高斯面,使其侧面与带电平面垂直,两底分别与带电平面平行,并位于离带电平面等距离的两侧如图1-1-3由高斯定律:
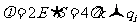

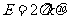
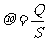
式中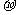 为电荷的面密度,由公式可知,无限大均匀带电平面两侧是匀强电场。
为电荷的面密度,由公式可知,无限大均匀带电平面两侧是匀强电场。
平行板电容器可认为由两块无限带电均匀导体板构成,其间场强为 ,则由场强叠加原理可知
,则由场强叠加原理可知
③均匀带电球壳的场强
有一半径为R,电量为Q的均匀带电球壳,如图1-1-4。由于电荷分布的对称性,故不难理解球壳内外电场的分布应具有球对称性,因此可在球壳内外取同心球面为高斯面。对高斯面1而言:
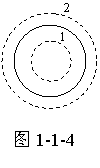
 ;
;
对高斯面2:
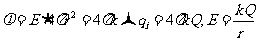 。
。
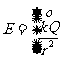
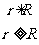
④球对称分布的带电球体的场强
推导方法同上,如图1-1-4,
对高斯面1,
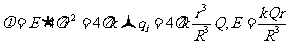 ;
;
对高斯面2,
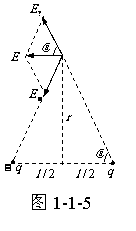
 。
。
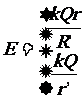
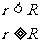
⑤电偶极子产生的电场
真空中一对相距为l的带等量异号电荷的点电荷系统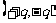 ,且l远小于讨论中所涉及的距离,这样的电荷体系称为电偶极子,并且把连接两电荷的直线称为电偶极子的轴线,将电量q与两点电荷间距l的乘积定义为电偶极矩。
,且l远小于讨论中所涉及的距离,这样的电荷体系称为电偶极子,并且把连接两电荷的直线称为电偶极子的轴线,将电量q与两点电荷间距l的乘积定义为电偶极矩。
a.设两电荷连线中垂面上有一点P,该点到两电荷连线的距离为r,则P点的场强如图1-1-5所示,其中
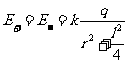
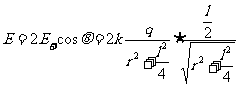
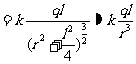
b.若 为两电荷延长线上的一点,
为两电荷延长线上的一点, 到两电荷连线中点的距离为r,如图1-1-6所示,
到两电荷连线中点的距离为r,如图1-1-6所示,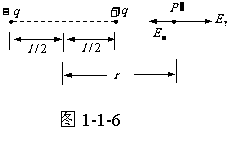 则
则
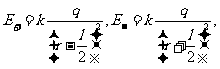
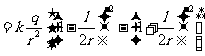
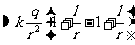

c.若T为空间任意一点,它到两电荷连线的中点的距离为r,如图1-1-7所示,则 在T点产生的场强分量为
在T点产生的场强分量为

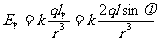 ,
,
由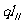 在T点产生的场强分量为
在T点产生的场强分量为
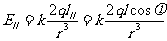
故
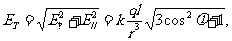
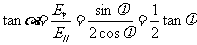
例2、如图所示,在-d≤x≤d的空间区域内(y,z方向无限延伸)均匀分布着密度为ρ的正电荷,此外均为真空
(1)试求 ≤d处的场强分布;
≤d处的场强分布;
(2)若将一质量为m,电量为 的带点质点,从x=d处由静止释放,试问该带电质点经过过多长时间第一次到达x=0处。
的带点质点,从x=d处由静止释放,试问该带电质点经过过多长时间第一次到达x=0处。
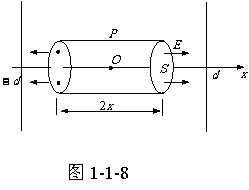 解: 根据给定区域电荷分布均匀且对称,在y、z方向无限伸展的特点,我们想象存在这样一个圆柱体,底面积为S,高为2x,左、右底面在x轴上的坐标分别是-x和x,如图1-1-8所示。可以判断圆柱体左、右底面处的场强必定相等,且方向分别是逆x轴方向和顺x轴方向。再根据高斯定理,便可求出坐标为x处的电场强度。
解: 根据给定区域电荷分布均匀且对称,在y、z方向无限伸展的特点,我们想象存在这样一个圆柱体,底面积为S,高为2x,左、右底面在x轴上的坐标分别是-x和x,如图1-1-8所示。可以判断圆柱体左、右底面处的场强必定相等,且方向分别是逆x轴方向和顺x轴方向。再根据高斯定理,便可求出坐标为x处的电场强度。
(1)根据高斯定律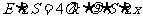 。坐标为x处的场强:
。坐标为x处的场强:
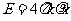 (
( ≤d),x>0时,场强与x轴同向,x<0时,场强与x轴反向。
≤d),x>0时,场强与x轴同向,x<0时,场强与x轴反向。
(2)若将一质量为m、电量为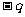 的带电质点置于此电场中,质点所受的电场力为:
的带电质点置于此电场中,质点所受的电场力为: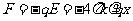 (
( ≤d)
≤d)
显然质点所受的电场力总是与位移x成正比,且与位移方向相反,符合准弹性力的特点。质点在电场力的运动是简谐振动,振动的周期为
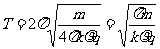
当质点从x=d处静止释放,第一次达到x=0处所用的时间为

§1、2电势与电势差
1.1.4、场强的叠加原理
在若干场源电荷所激发的电场中任一点的总场强,等于每个场源电荷单独存在时在该点所激发的场强的矢量和。
原则上讲,有库仑定律和叠加原理就可解决静电学中的全部问题。
例1、如图1-1-1(a)所示,在半径为R、体电荷密度为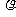 的均匀
的均匀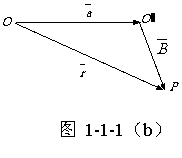 带电球体内部挖去半径为
带电球体内部挖去半径为 的一个小球,小球球心
的一个小球,小球球心 与大球球心O相距为a,试求
与大球球心O相距为a,试求 的电场强度,并证明空腔内电场均匀。
的电场强度,并证明空腔内电场均匀。
分析: 把挖去空腔的带电球看作由带电大球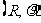 与带异号电的小球
与带异号电的小球 构成。由公式求出它们各自在
构成。由公式求出它们各自在 的电场强度,再叠加即得
的电场强度,再叠加即得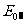 。这是利用不具有对称性的带电体的特点,把它凑成由若干具有对称性的带电体组成,使问题得以简化。
。这是利用不具有对称性的带电体的特点,把它凑成由若干具有对称性的带电体组成,使问题得以简化。
在小球内任取一点P,用同样的方法求出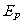 ,比较
,比较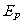 和
和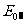 ,即可证明空腔内电场是均匀的。采用矢量表述,可使证明简单明确。
,即可证明空腔内电场是均匀的。采用矢量表述,可使证明简单明确。
解: 由公式可得均匀带电大球(无空腔)在 点的电场强度
点的电场强度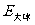 ,
,
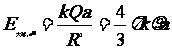 ,方向为O指向
,方向为O指向 。
。
同理,均匀带异号电荷的小球  在球心
在球心 点的电场强度
点的电场强度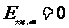
所以 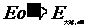
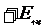 ,
,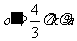
 如图1-1-1(b)所示,在小球内任取一点P,设从O点到
如图1-1-1(b)所示,在小球内任取一点P,设从O点到 点的矢量为
点的矢量为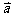 ,
, 为
为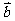 ,OP为
,OP为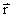 。则P点的电场强度
。则P点的电场强度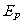 为
为
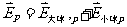

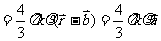
可见: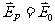
因P点任取,故球形空腔内的电场是均匀的。
1.1.3、电场强度
电场强度是从力的角度描述电场的物理量,其定义式为
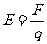
式中q是引入电场中的检验电荷的电量,F是q受到的电场力。
借助于库仑定律,可以计算出在真空中点电荷所产生的电场中各点的电场强度为

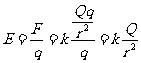
式中r为该点到场源电荷的距离,Q为场源电荷的电量。
1.1.2、库仑定律
真空中,两个静止的点电荷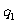 和
和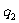 之间的相互作用力的大小和两点电荷电量的乘积成正比,和它们之间距离r的平方成正比;作用力的方向沿它们的连线,同号相斥,异号相吸
之间的相互作用力的大小和两点电荷电量的乘积成正比,和它们之间距离r的平方成正比;作用力的方向沿它们的连线,同号相斥,异号相吸
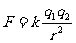
式中k是比例常数,依赖于各量所用的单位,在国际单位制(SI)中的数值为: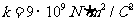 (常将k写成
(常将k写成 的形式,
的形式,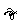 是真空介电常数,
是真空介电常数,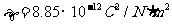 )
)
库仑定律成立的条件,归纳起来有三条:(1)电荷是点电荷;(2)两点电荷是静止或相对静止的;(3)只适用真空。
条件(1)很容易理解,但我们可以把任何连续分布的电荷看成无限多个电荷元(可视作点电荷)的集合,再利用叠加原理,求得非点电荷情况下,库仑力的大小。由于库仑定律给出的是一种静电场分布,因此在应用库仑定律时,可以把条件(2)放宽到静止源电荷对运动电荷的作用,但不能推广到运动源电荷对静止电荷的作用,因为有推迟效应。关于条件(3),其实库仑定律不仅适用于真空,也适用于导体和介质。当空间有了导体或介质时,无非是出现一些新电荷--感应电荷和极化电荷,此时必须考虑它们对源电场的影响,但它们也遵循库仑定律。
1.1.1、电荷守恒定律
大量实验证明:电荷既不能创造,也不能被消灭,它们只能从一个物体转移到另一个物体,或者从物体的一部分转移到另一部分,正负电荷的代数和任何物理过程中始终保持不变。
我们熟知的摩擦起电就是电荷在不同物体间的转移,静电感应现象是电荷在同一物体上、不同部位间的转移。此外,液体和气体的电离以及电中和等实验现象都遵循电荷守恒定律。
2.2.5、波粒二象性
由理论和实验所得结果证明,描述粒子特征的物理量(E,p)与描述波动特征的物理量(v,λ)之间存在如下关系。
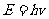
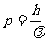
事实上,这种二象性是一切物质(包括实物和场)所共有的特征。
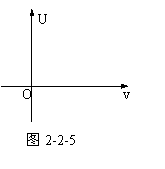
例1、图5-1中纵坐标为光电效应实验中所加电压(U),横坐标为光子的频率(v)。若某金属的极限频率为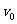 ,普朗克恒量为h,电子电量为e,试在图中画出能产生光电流的区域(用斜线表示)。
,普朗克恒量为h,电子电量为e,试在图中画出能产生光电流的区域(用斜线表示)。
分析:在U-v图第一象限中能产生光电流的区域,可根据极限频率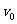 很容易地作出。关键在于如何确定第四象限中能产生光电流的区域,但我们可以利用爱因斯坦的光电方程找出这一区域。
很容易地作出。关键在于如何确定第四象限中能产生光电流的区域,但我们可以利用爱因斯坦的光电方程找出这一区域。
解:爱因斯坦的光电方程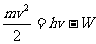 . ①
. ①
根据极限频率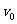 可知
可知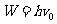 ②
②
 由于光电子具有最大初动能为
由于光电子具有最大初动能为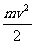 ,则它可克服反向电压作功为Ue,故有图5-1
,则它可克服反向电压作功为Ue,故有图5-1
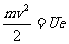 ③
③
将②、③式代入①式可得
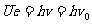
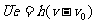
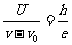
此即为图2-2-5中BC斜率的绝对值。据此可作出图2-2-6,图中画有斜线区域即为能产生光电流的区域。
例2、一光电管阴极对于波长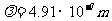 的入射光,发射光电子的遏止电压为0.71V,当入射光的波长为多少时,其遏止电压变为1.43V?(电子电量
的入射光,发射光电子的遏止电压为0.71V,当入射光的波长为多少时,其遏止电压变为1.43V?(电子电量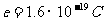 ,普朗克常量
,普朗克常量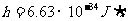 )。
)。
分析:根据爱因斯坦的光电方程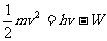 ,可知,当加在光电管上的反向电压达到一定值时可有Ue=hv-W,此时光电管无光电流产生,这个电压U即为遏止电压。知道了遏止电压U即可由光电方程求出逸出功W。对于一个光电管,它的阴极逸出功W是不变的,因而也可利用W求出对应不同遏止电压的入射光的频率(或波长)。
,可知,当加在光电管上的反向电压达到一定值时可有Ue=hv-W,此时光电管无光电流产生,这个电压U即为遏止电压。知道了遏止电压U即可由光电方程求出逸出功W。对于一个光电管,它的阴极逸出功W是不变的,因而也可利用W求出对应不同遏止电压的入射光的频率(或波长)。
解:光电方程为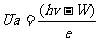 ,式中U
,式中U 为遏止电压,W为阴极材料的逸出功,v为入射光的频率。设所求入射光的波长为
为遏止电压,W为阴极材料的逸出功,v为入射光的频率。设所求入射光的波长为 ,将
,将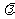 和
和 两次代入光电方程,消去逸出功W,得
两次代入光电方程,消去逸出功W,得
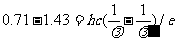
代入数据得 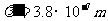
例3、一波长为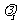 的光子与一运动的自由电子碰撞。碰撞的结果使电子变为静止,并且波长为
的光子与一运动的自由电子碰撞。碰撞的结果使电子变为静止,并且波长为 的光子在与原先方向的夹角为
的光子在与原先方向的夹角为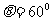 的方向上前进。此光子员另一静止的自由电子碰撞,然后以波长
的方向上前进。此光子员另一静止的自由电子碰撞,然后以波长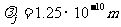 的光子前进,其方向在碰撞后改变了
的光子前进,其方向在碰撞后改变了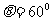 。计算第一个电子在碰撞前的德布罗意波长。(普朗克常数
。计算第一个电子在碰撞前的德布罗意波长。(普朗克常数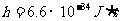 ,电子质量
,电子质量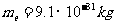 ,光速
,光速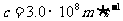 )
)
分析:此题需运用能量守恒与动量守恒求解,但必须应用相对论作必要的变换。
解:对第一次碰撞,能量守恒定律为
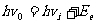 ①
①
式中v是光子的频率,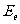 是电子的能量。在波长为
是电子的能量。在波长为 的光子的出射方向,以及在与它垂直方向上写出动量守恒定律(见图2-2-7)分别为
的光子的出射方向,以及在与它垂直方向上写出动量守恒定律(见图2-2-7)分别为
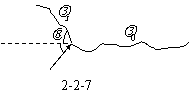

式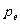 是电子的动量。
是电子的动量。
从上述两方程消去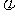 ,并把λ写成c/v,有
,并把λ写成c/v,有
 ②
②
利用相对论关系
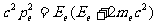 ③
③
以及方程①和②得
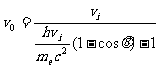 ④
④
变换后得
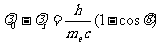 ⑤
⑤
对第二次碰撞可作同样的计算,得如下结果
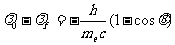 ⑥
⑥
⑤⑥两式相减,得
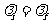
两次碰撞是类似的,利用⑤式得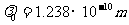 。
。
分别利用①和③式,可算出电子的能量和动量为
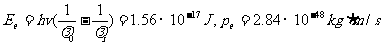
第一个电子的波长为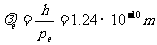 。
。
例4、一台二氧化碳气体激光器发出的激光功率为P=1000W,射出的光束截面积为A=1.00mm2。试问:
(1)当该光束垂直入射到一物体平面上时,可能产生的光压的最大值为多少?
(2)这束光垂直射到温度T为273K,厚度d为2.00cm的铁板上,如果有80%的光束能量被激光所照射到的那一部分铁板所吸收,并使其熔化成与光束等截面积的直圆柱孔,这需要多少时间?
已知,对于波长为λ的光束,其每一个光子的动量为k=h/λ,式中h为普朗克恒量,铁的有关参数为:热容量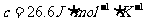 ,密度
,密度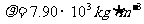 ,熔点
,熔点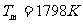 ,熔解热
,熔解热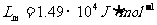 ,摩尔质量
,摩尔质量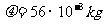 。
。
分析:光压即光对被照射物产生的压强,而求压强的关键在求出压力。利用动量定理,可由光子的动量变化求出它对被照射物的压力。
解:(1)当光束垂直入射到一个平面上时,如果光束被完全反射,且反射光垂直于平面,则光子的动量改变达最大值
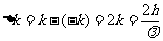 ①
①
此时该光束对被照射面的光压为最大。设单位时间内射到平面上的光子数为n,光压p的数值就等于这些光子对被照射面积A的冲量(也就是光子动量的改变量)的总和除以面积A,即
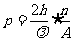 ②
②
每个光子的能量为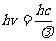 ,这里c为真空中的光速,v为光的频率,因而
,这里c为真空中的光速,v为光的频率,因而
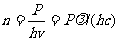
于是,由②式
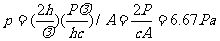
(2)激光所照射到的质量为M那一小部分铁板在熔化过程中所吸收的热量为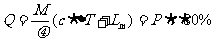
所以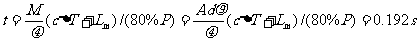
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com