
2.6.2、 惯性质量和引力质量 根据牛顿运动定律,力一定时,物体的加速度与质量成反比,牛顿定律中的质量度量了物体的惯性,称为惯性质量,以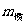 为符号,有
为符号,有
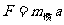
根据万有引力定律,两物体(质点)间的引力和它们的质量乘积成正比。万有引力定律中的质量,类似于库仑定律中的电荷,称为引力质量,以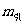 为符号。
为符号。
惯性质量和引力质量是两个不同的概念,没有必然相等的逻辑关系,它们是否相等,应由实验来检验。本世纪初,匈牙利物理学家厄缶应用扭秤证明,只要单位选择恰当,惯性质量和引力质量相等,实验精度达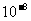 。后来,人们又把两者相等的实验精度提高到
。后来,人们又把两者相等的实验精度提高到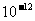 。
。
设一物体在地面上做自由落体运动,此物体的惯性质量和引力质量分别为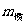 和
和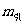 ,以
,以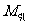 代表地球的引力质量,根据万有引力定律和牛顿第二定律,有
代表地球的引力质量,根据万有引力定律和牛顿第二定律,有
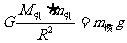 ,
,
式中G为万有引力常量,R为地球半径,g为物体下落的加速度。因为 ,所以
,所以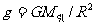 ,与物体的质量无关。这就是伽利略自由落体实验的结论。
,与物体的质量无关。这就是伽利略自由落体实验的结论。
既然惯性质量与引力质量相等,就可以简单地应用质量一词,并应用相同的单位。质量也度量了物质的多少。
2.6.1、 非惯性系与惯性力 牛顿运动定律在惯性系里才成立,在相对惯性系做加速运动的参照系(称非惯性系)里,会出现什么情况呢?例如,在一列以加速度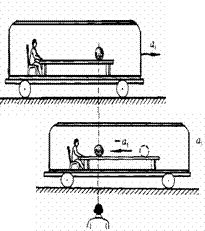
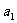 做直线运动的车厢里,有一个质量为m的小球,小球保持静止状态,小球所受合外力为零,符合牛顿运动定律。相对于非惯性系的车厢来观测,小球以加速度-
做直线运动的车厢里,有一个质量为m的小球,小球保持静止状态,小球所受合外力为零,符合牛顿运动定律。相对于非惯性系的车厢来观测,小球以加速度-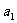 向后运动,而小球没有受到其他物体力的作用,牛顿运动定律不再成立。
向后运动,而小球没有受到其他物体力的作用,牛顿运动定律不再成立。
不过,车厢里的人可以认为小球受到一向后的力,把牛顿运动定律写为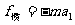 。这样的力不是其他物体的作用,而是由参照系是非惯性系所引起的,称为惯性力。如果一非惯性系以加速度
。这样的力不是其他物体的作用,而是由参照系是非惯性系所引起的,称为惯性力。如果一非惯性系以加速度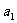 相对惯性系而运动,则在此非惯性里,任一质量为m的物体受到一惯性力
相对惯性系而运动,则在此非惯性里,任一质量为m的物体受到一惯性力 ,把惯性力
,把惯性力 计入在内,在非惯性里也可以应用牛顿定律。当汽车拐弯做圆周运动时,相对于地面出现向心加速度
计入在内,在非惯性里也可以应用牛顿定律。当汽车拐弯做圆周运动时,相对于地面出现向心加速度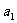 ,相对于车厢人感觉向外倾倒,常说受到了离心力,正确地说应是惯性离心力,这就是非惯性系中出现的惯性力。
,相对于车厢人感觉向外倾倒,常说受到了离心力,正确地说应是惯性离心力,这就是非惯性系中出现的惯性力。
2.5.6、相对论的速度叠加
由于时间和空间的相对性,对于物体的速度,在某一惯性系 内观测,要用
内观测,要用 系的时间和空间坐标表示;在另一惯性系S内观测,要用S系的时间和空间坐标表示。这样,速度叠加公式就不再是绝对时空的速度叠加公式了。假如
系的时间和空间坐标表示;在另一惯性系S内观测,要用S系的时间和空间坐标表示。这样,速度叠加公式就不再是绝对时空的速度叠加公式了。假如 和S两系的坐标轴相平行,
和S两系的坐标轴相平行, 以速度v沿x轴而运动,一质点以
以速度v沿x轴而运动,一质点以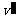 相对
相对 沿
沿 轴而运动,则相对S,其速度u为
轴而运动,则相对S,其速度u为
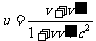
这是相对论的速度叠加公式。如果 ,则u<c;如果
,则u<c;如果 (光速),则u=c。与相对论的时空概念相协调。
(光速),则u=c。与相对论的时空概念相协调。
§2、6、广义相对论初步
狭义相对论在惯性系里研究物理规律,不能处理引力问题。
1915年,爱因斯坦在数学家的协助下,把相对性原理从惯性系推广到任意参照系,发表了广义相对论。由于这个理论过于抽象,数学运算过于复杂,这里只做个大概描述。
2.5.5、相对论的动力学的基本方程
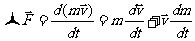
2.5.4、相对论能量、动量的关系
(1)
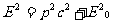
若以 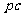 、
、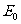 表示一直角三角形的两条直角边,则E必构成此直角三角形的斜边。
表示一直角三角形的两条直角边,则E必构成此直角三角形的斜边。
(2)
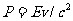
2.5.3、相对论动量
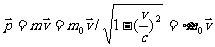
2.5.2、相对论能量
(1)物体的总能量 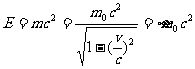
式(18-19)表明:一定的质量必定联系着一定的能量,反之一定的能量必定联系着一定的质量。这个方程就叫做爱因斯坦质能(联系)方程。既然物体的质量与能量有一定的对应关系,所以在相对论力学中质量守恒与能量守恒等价。
(2)物体的静能
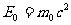
(3)物体的相对论动能 
(4)质能变化方程: 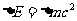
上式告诉我们当物体的质量发生 的变化时,必同时伴随着能量的变化
的变化时,必同时伴随着能量的变化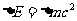 。
。
2.5.1、 相对论质量
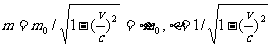
式(18-18)中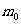 为物体的静止质量,v为物体的运到速度,c为真空中的光速。此式告诉我们在狭义相对论中物体的质量不再是一个恒量,而是一个随速度变化的物理量。当
为物体的静止质量,v为物体的运到速度,c为真空中的光速。此式告诉我们在狭义相对论中物体的质量不再是一个恒量,而是一个随速度变化的物理量。当 时,
时, ,而当
,而当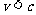 时,
时,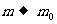 。因此一个有限大小的力作用于静止质量无论如何小的物体上,其速度不可能趋近于无限大,物体的极限速度为c。
。因此一个有限大小的力作用于静止质量无论如何小的物体上,其速度不可能趋近于无限大,物体的极限速度为c。
2.4.3、 相互作用的最大传播速度和因果律 由同时的相对性可知,事件的先后次序与它们的空间位置和两惯性系间的运动状态有关。在经典的时空理论中,时间的次序是绝对的。在相对论时空观中,是否事件的先后次序没有客观意义呢?显然不是的,如果两事件有因果关系(如农样生产中,先播种后收获,人的先生后死),则它们的先后次序应当是绝对的,不容颠倒,这是事件先后这个概念所必须反映的客观内容。相对论在什么条件下才与这个条件一致呢?
设两事件的时空坐标在S系中为(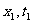 )和(
)和(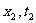 ) ,在
) ,在 系中为(
系中为(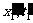 ) 和(
) 和(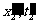 ) ,由洛仑兹变换有
) ,由洛仑兹变换有
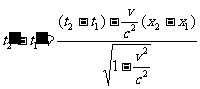 .
.
如果两事件有因果关系,而且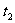 >
>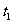 ,由于它们的次序不能颠倒,必须在
,由于它们的次序不能颠倒,必须在 系中观察时,亦有
系中观察时,亦有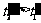 。这就要求
。这就要求
 ,
,
即
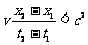 .
.
因为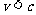 ,满足上式的条件是
,满足上式的条件是
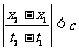 .
.
对于因果事件,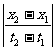 正是事件进展的速度,因此因果事件先后次序的绝对性对相对论的要求是:所有物体的运动速度、讯号传输的速度是光速c。
正是事件进展的速度,因此因果事件先后次序的绝对性对相对论的要求是:所有物体的运动速度、讯号传输的速度是光速c。
同时的相对性 在惯性系S中异地同时发生两个事件:事件1(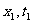 ),事件2(
),事件2(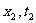 ) ,且
) ,且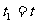
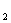 (设y,z不变,故事件只用x, t表示)。在另一惯性系中看这两事件的时空坐标为1:(
(设y,z不变,故事件只用x, t表示)。在另一惯性系中看这两事件的时空坐标为1:(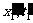 )与2:(
)与2:(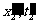 )。由洛仑兹变换关系
)。由洛仑兹变换关系
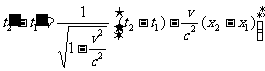
=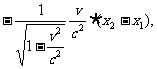
只要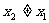 ,则
,则 。就是说在S系中同时发生的两事件,在
。就是说在S系中同时发生的两事件,在 系看却不同时,即在某惯性系内不同地点同时发生的两事件,对具有相对运动的另一惯性系内的观察者说来,他所测得的两个事件发生的时刻是不同的,同时是相对的。
系看却不同时,即在某惯性系内不同地点同时发生的两事件,对具有相对运动的另一惯性系内的观察者说来,他所测得的两个事件发生的时刻是不同的,同时是相对的。
§2、5、相对论动力学基础
2.4.2、 运动尺度缩短 设一棍静止在 系中,沿
系中,沿  轴放置,且
轴放置,且 系想对于S系以匀速v沿x方向运动。在
系想对于S系以匀速v沿x方向运动。在 系的观察者观察,棍后端的坐标为
系的观察者观察,棍后端的坐标为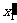 ,前端的坐标为
,前端的坐标为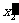 ,棍对他没有运动,因此他测得棍长为
,棍对他没有运动,因此他测得棍长为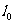 =
=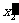 -
-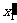 。S系的观察者观察到在同一时刻t,棍后端的坐标为
。S系的观察者观察到在同一时刻t,棍后端的坐标为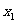 ,前端的坐标为
,前端的坐标为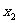 ,则他测得棍长为
,则他测得棍长为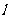 =
=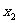 -
-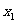 ,根据洛仑兹变换
,根据洛仑兹变换
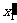 =
=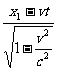 ,
,
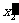 =
=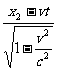 .
.
两式相减,得
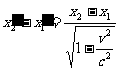 ,
,
即
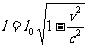 .
.
这表示物体沿其长度方向运动时,其长度缩短为静止时的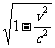 倍。这种现象称为洛仑兹收缩。缩短是相对的,每一惯性系都测得对它运动着的物体沿运动方向的长度要缩短。
倍。这种现象称为洛仑兹收缩。缩短是相对的,每一惯性系都测得对它运动着的物体沿运动方向的长度要缩短。
运动物体沿运动方向的长度缩短是时空的一种基本属性,不但物体的长度缩短,物体间的距离也要缩短,所以这种收缩不是物体内部结构的改变。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com