
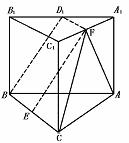
317. 如图,A1B1C1-ABC是直三棱柱,∠BCA=90°,点D1,F1分别是A1B1,A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
A. B.
B.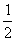 C.
C. D.
D.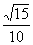
解 连D1F1,则D1F1⊥A1C1,又BC⊥CA,所以BD1在平面ACC1A1内的射影为CF1,设AC=2a,则BC=CC1=2a.取BC的中点E,连EF1,则EF∥BD1.
∴cosθ1=cos∠EF1C= =
= =
= ,
,
cosθ2=cos∠AF1C=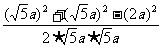 =
=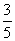 ,
,
∴
cosθ=cosθ1·cosθ2= ·
·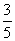 =
= ,应选A.
,应选A.
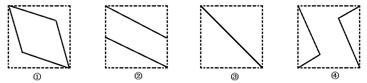
316. 如图,E、F分别是正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是 (要求:把可能的图的序号都填上)

解 ∵四边形BFD1E在正方体的一对平行面上的投影图形相同,在上、下底面上,E、F的射影在棱的中点,四边形的投影图形为②,在左右侧面上,E、F的连线垂直侧面,从而四边形的投影图形为③,在前后侧面上四边形投影图形也为②.故应填②③.
315.经过一个角的顶点引这个角所在平面的斜线,如果斜线和这个角两边的夹角相等,那么斜线在平面上的射影是这个角的平分线所在的直线.
已知:∠ABC α,P
α,P α,∠PBA=∠PBC,PQ⊥α,Q∈α,如图.
α,∠PBA=∠PBC,PQ⊥α,Q∈α,如图.

求证:∠QBA=∠QBC
证:PR⊥AB于R,PS⊥BC于S.
则:∠PRB=∠PSB=90°.
∵PB=PB.∠PBR=∠PBS
∴RtΔPRB≌RtΔPSB
∴PR=PS
∵点Q是点P在平面α上的射影.
∴QR=QS
又∵QR⊥AB,QS⊥BC
∴∠ABQ=∠CBQ
314.求证:两条平行线和同一条平面所成的角相等.
已知:a∥b,a∩α=A1,b∩β=B1,∠θ1、∠θ2分别是a、b与α所成的角.如图,求证:∠θ1=∠θ2.
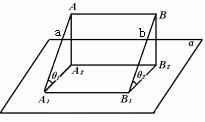
证:在a、b上分别取点A、B.如图,且AA1=BB1,连结AB和A1B1.
∵AA1∥BB1
∴四边形AA1B1B是平行四边形.∴AB∥A1B1
又A1B1 α ∴AB∥α.
α ∴AB∥α.
设AA2⊥α于A2,BB2⊥α于B2,则AA2=BB2
在RtΔAA1A2与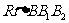 中 AA2=BB2,AA1=BB1
中 AA2=BB2,AA1=BB1
∴RtΔAA1A2≌RtΔBB1B2
∴∠AA1A2=∠BB1B2
即 ∠θ1=∠θ2.
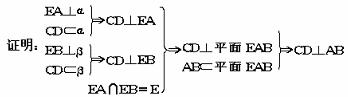
313..已知:α∩β=CD,EA⊥α,EB⊥β,求证:CD⊥AB.
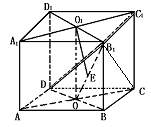
312. 正方体ABCD-A1B1C1D1的棱长为a,求A1C1和平面AB1C间的距离.
解法1 如图所示,A1C1∥平面AB1C,又平面BB1DD1⊥平面AB1C.
故若过O1作O1E⊥OB1于E,则OE1⊥平面AB1C,O1E为所求的距离
由O1E·OB1=O1B1·OO1,
可得:O1E=
解法2:转化为求C1到平面AB1C的距离,也就是求三棱锥C1-AB1C的高h.
由 V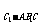 =V
=V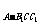 ,可得h=
,可得h=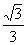 a.
a.
解法3 因平面AB1C∥平面C1DA1,它们间的距离即为所求,连BD1,分别交B1O、DO1与F、G(图中未画出)。易证BD1垂直于上述两个平面,故FG长即为所求,易求得
FG= .
.
点评 (1)求线面距离的先决条件是线面平行,而求线面距离的常用方法是把它们转化为求点面之间的距离,有时也可转化为求面面距离,从本题的解法也可悟出求异面直线之间的距离的思路.
311. 如图,在棱长为a的正方体AC1中,M是CC1的中点,点E在AD上,且AE=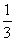 AD,F在AB上,且AF=
AD,F在AB上,且AF=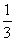 AB,求点B到平面MEF的距离.
AB,求点B到平面MEF的距离.
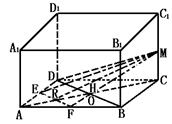
解法一:设AC与BD交于O点,EF与AC交于R点,由于EF∥BD所以将B点到面MEF的距离转化为O点到面MEF的距离,面MRC⊥面MEF,而MR是交线,所以作OH⊥MR,即OH⊥面MEF,OH即为所求.
∵OH·MR=OR·MC,
∴OH=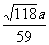 .
.
解法二:考察三棱锥B-MEF,由VB-MEF=VM-BEF可得h.
点评 求点面的距离一般有三种方法:
①利用垂直面;
②转化为线面距离再用垂直面;
③当垂足位置不易确定时,可考虑利用体积法求距离.
175.( ) My father has a computer, but he doesn’t know to use it.
(2010四川达州市)
A. what B. how C. who D. which
174.( ) --- Can I help you dear?
--- Yeah, I don’t know ______ a banana milk shake. Maybe you can teach me.
(2010浙江宁波市)
A. what to do B. when to make C. how to make D. why to do
173.( ) The little boy ____ by the big one this morning. (2010新疆阜康市)
A. was made to cry B. was made cry C. made to cry D. made cry
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com