
上一节,我们了解了数学建模的方法、函数的拟合和较简单的情形,并总结了解答应用题的基本步骤,这一节,我们继续学习有关数学建模的方法,加强大家的函数应用意识.
6.强化“分类思想”应用。指数函数与对数函数的性质均与其底数是否大于1有关;对于根式的意义及其性质的讨论要分清n是奇数还是偶数等。
5.实施“定义域优先”原则。函数的定义域是函数最基本的组成部分,任何对函数性质的研究都离不开函数的定义域。例如,求函数的单调区间,必须在定义域范围内;通过求出反函数的定义域,可得到原函数的值域;定义域关于原点对称,是函数为奇函数或偶函数的必要条件。为此,应熟练掌握求函数定义域的原则与方法,并贯彻到解题中去。
4.重视“数形结合”渗透。“数缺形时少直观,形缺数时难入微”。当你所研究的问题较为抽象时,当你的思维陷入困境时,当你对杂乱无章的条件感到头绪混乱时,一个很好的建议便是:画个图!利用图形的直观性,可迅速地破解问题,乃至最终解决问题。
3.活用“定义法”解题。定义是一切法则与性质的基础,是解题的基本出发点。利用定义,可直接判断所给的对应是否满足映射或函数的条件,证明或判断函数的单调性与奇偶性并写出函数的单调区间等。
2.涉及本单元知识点的高考题,综合性大题不多.所以在复习中不宜做过多过高的要求,只要灵活掌握小型综合题型(如集合与映射,集合与自然数集,集合与不等式,集合与方程等,充分条件与必要条件与三角、立几、解几中的知识点的结合等) 映射的概念以选择题型出现,难度不大。就可以了
1.在复习中首先把握基础性知识,深刻理解本单元的基本知识点、基本数学思想和基本数学方法.重点掌握集合、充分条件与必要条件的概念和运算方法.要真正掌握数形结合思想--用文氏图解题.
(二)2010年高考预测
1.集合是每年高考必考的知识点之一。题型一般是选择和填空的形式,主要考查集合的运算和求有限集合的子集及其个数.
2.简易逻辑是一个新增内容,据其内容的特点,在高考中应一般在选择题、填空题中出现,如果在解答题中出现,则只会是中低档题.
3.集合、简易逻辑知识,作为一种数学工具,在函数、方程、不等式、排列组合及曲线与方程等方面都有广泛的运用,高考题中常以上面内容为载体,以集合的语言为表现形式,结合简易逻辑知识考查学生的数学思想、数学方法和数学能力,题型常以解答题的形式出现.
(一)思想方法总结
1. 数形结合
2. 分类讨论
8、证明命题条件的充要性时,既要证明原命题成立(即条件的充分性),又要证明它的逆命题成立(即条件的必要性).
例10、(2008安徽卷) 是方程
是方程 至少有一个负数根的( )
至少有一个负数根的( )
A.必要不充分条件 B.充分不必要条件
C.充分必要条件 D.既不充分也不必要条件
解:当 ,得a<1时方程有根。a<0时,
,得a<1时方程有根。a<0时,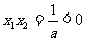 ,方程有负根,又a=1时,方程根为
,方程有负根,又a=1时,方程根为 ,所以选(B)。
,所以选(B)。
例11、(2008湖北卷)若集合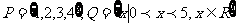 ,则:( )
,则:( )
A. 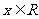 是
是 的充分条件,不是
的充分条件,不是 的必要条件
的必要条件
B. 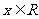 不是
不是 的充分条件,是
的充分条件,是 的必要条件
的必要条件
C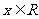 是
是 的充分条件,又是
的充分条件,又是 的必要条件.
的必要条件.
D.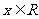 既不是
既不是 的充分条件,又不是
的充分条件,又不是 的必要条件
的必要条件
解: 反之不然故选A
反之不然故选A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com